MTH 161 Introduction To Statistics Lecture 28 Dr

MTH 161: Introduction To Statistics Lecture 28 Dr. MUMTAZ AHMED

Review of Previous Lecture In last lecture we discussed: � Finding Area Under Normal Curve using MS-Excel � Normal Approximation to Binomial Distribution � Central Limit Theorem � Related examples 2

Objectives of Current Lecture In the current lecture: � Joint Distributions � Moment Generating Functions � Covariance � Related Examples 3

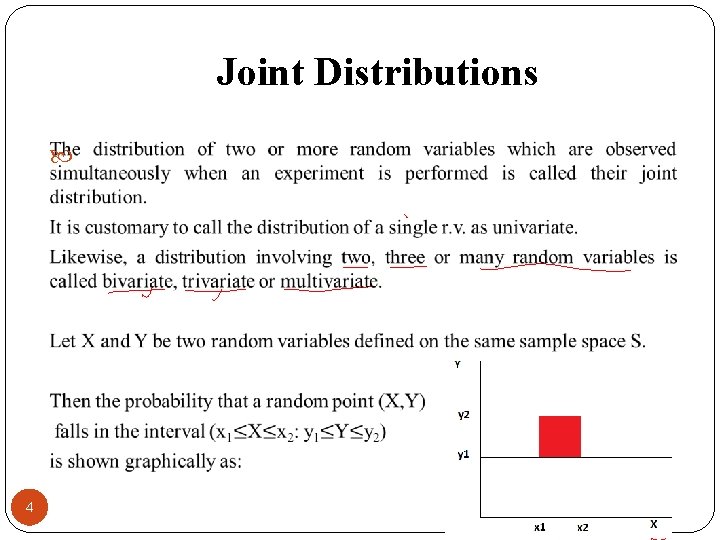
Joint Distributions 4

Joint Distributions Types of Joint Distribution: � Discrete � Continuous � Mixed A bivariate distribution may be discrete when The possible values of (X, Y) are finite or countably infinite. It is continuous if (X, Y) can assume all values in some non-countable set of plane. 5 It is said to be mixed if one r. v. is discrete and other is continuous.

Discrete Joint Distributions 6

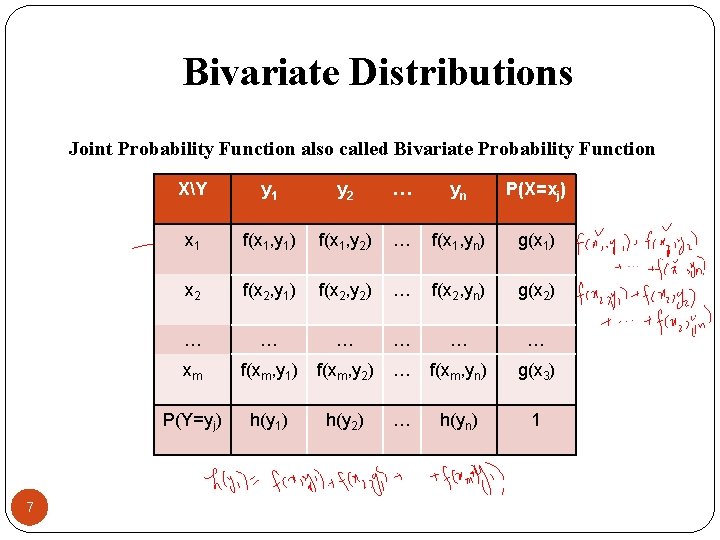
Bivariate Distributions Joint Probability Function also called Bivariate Probability Function 7 XY y 1 y 2 … yn P(X=xj) x 1 f(x 1, y 1) f(x 1, y 2) … f(x 1, yn) g(x 1) x 2 f(x 2, y 1) f(x 2, y 2) … f(x 2, yn) g(x 2) … … … xm f(xm, y 1) f(xm, y 2) … f(xm, yn) g(x 3) P(Y=yj) h(y 1) h(y 2) … h(yn) 1

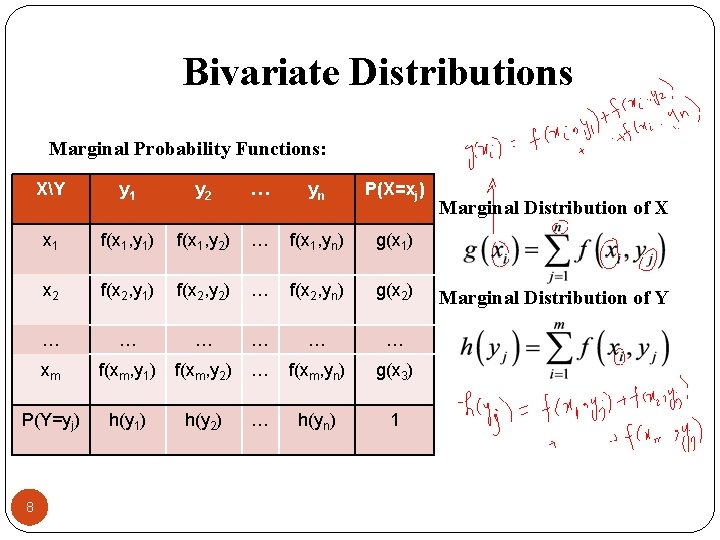
Bivariate Distributions Marginal Probability Functions: XY y 1 y 2 … yn P(X=xj) x 1 f(x 1, y 1) f(x 1, y 2) … f(x 1, yn) g(x 1) x 2 f(x 2, y 1) f(x 2, y 2) … f(x 2, yn) g(x 2) … … … xm f(xm, y 1) f(xm, y 2) … f(xm, yn) g(x 3) P(Y=yj) h(y 1) h(y 2) … h(yn) 1 8 Marginal Distribution of X Marginal Distribution of Y

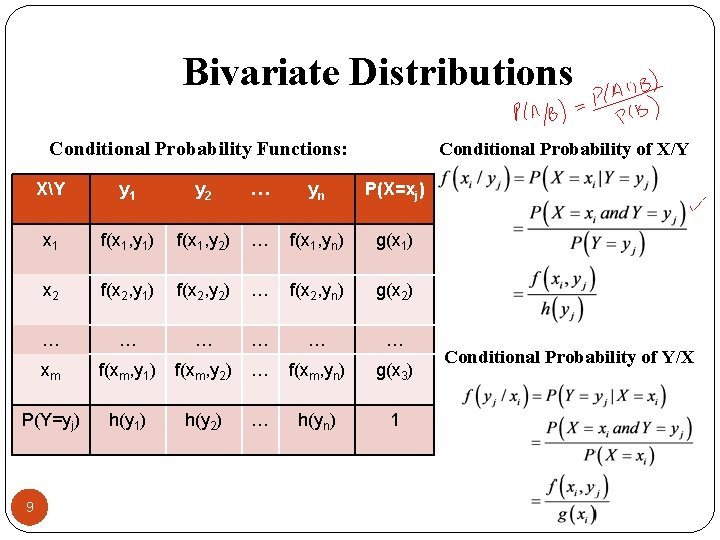
Bivariate Distributions Conditional Probability Functions: Conditional Probability of X/Y XY y 1 y 2 … yn P(X=xj) x 1 f(x 1, y 1) f(x 1, y 2) … f(x 1, yn) g(x 1) x 2 f(x 2, y 1) f(x 2, y 2) … f(x 2, yn) g(x 2) … … … xm f(xm, y 1) f(xm, y 2) … f(xm, yn) g(x 3) P(Y=yj) h(y 1) h(y 2) … h(yn) 1 9 Conditional Probability of Y/X

Bivariate Distributions Independence: Two r. v. s X and Y are said to be independent iff for all possible pairs of values (xi, yj), the joint probability function f(x, y) can be expressed as the product of the two marginal probability functions. 10

Bivariate Distributions Example: An urn contains 3 black, 2 red and 3 green balls and 2 balls are selected at random from it. If X is the number of black balls and Y is the number of red balls selected, then find the joint probability distribution of X and Y. Solution: Total Balls=3 black+2 red+3 green=8 balls Possible values of both X & Y are={0, 1, 2} The Joint Frequency Distribution 11 XY 0 1 2 g(x) 0 3/28 6/28 10/28 1 9/28 6/28 0 15/28 2 3/28 0 0 3/28 H(y) 15/28 12/28 1

Bivariate Distributions The Joint Frequency Distribution XY 0 1 2 g(x) 0 3/28 6/28 10/28 1 9/28 6/28 0 15/28 2 3/28 0 0 3/28 H(y) 15/28 12/28 1 P(X=0 |Y=1)=? 12 P(X+Y<=1)=? P(X+Y<=1)=f(0, 0)+f(0, 1)+f(1, 0) =3/28+6/28+9/28=18/28

Moment Generating Function The moment-generating function of a random variable is an alternative specification of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly functions or cumulative distribution functions. with probability density In addition to univariate distributions, moment-generating functions can be multivariate distributions, and can even be extended to more general cases. There are relations between the behavior of the moment-generating function of a distribution and properties of the distribution. 13

Moment Generating Function 14

Moment Generating Functions of some important distributions: � If X is a Bernoulli r. v. with parameter p: � If X is a Binomial r. v. with parameters n and p: � If X is a Poisson r. v. with parameters λ: � If X is a Normal r. v. with parameters and σ2: 15

Characteristic Function The M. G. F. doesn’t exist for many probability distributions. We then use another function, called characteristic function (c. f. ). The characteristic function of a r. v. is defined as: 16

Covariance 17

Covariance ranges between minus infinity to plus infinity. The covariance is positive if the deviations of the two variables from their respective means tend to have the same sign and negative if the deviations tend to have opposite signs. � A positive covariance indicates a positive association between the two variables. � A negative covariance indicates a negative association between the two variables. � A zero covariance indicates neither positive nor negative association between the two variables. 18

Covariance Sample Covariance can be written as: 19

Variance of Sum or Difference of r. v. ’s Let X and Y be two r. v. ’s, then: 20

Review Let’s review the main concepts: � Joint Distributions � Moment Generating Functions � Covariance � Related Examples 21

Next Lecture In next lecture, we will study: � Describing Bivariate Data � Scatter Plot � Concept of Correlation � Properties of Correlation � Related examples and Excel Demo 22