MTH 161 Introduction To Statistics Lecture 08 Dr

MTH 161: Introduction To Statistics Lecture 08 Dr. MUMTAZ AHMED

Review of Previous Lecture In last lecture we discussed: � Creating Charts in MS-Excel �Histogram �Scatter Plot � Use of Excel Add-ins �Activating Excel Add-ins �Using Data Analysis Excel Add-in � Measures of Central Tendency � Characteristics of a good average �Mean � Mean 2 for ungrouped Data � Mean for grouped Data

Objectives of Current Lecture Measures of Central Tendency �Weighted Mean �Combined Mean �Merits and demerits of Arithmetic Mean � Median �Median for Ungrouped Data 3

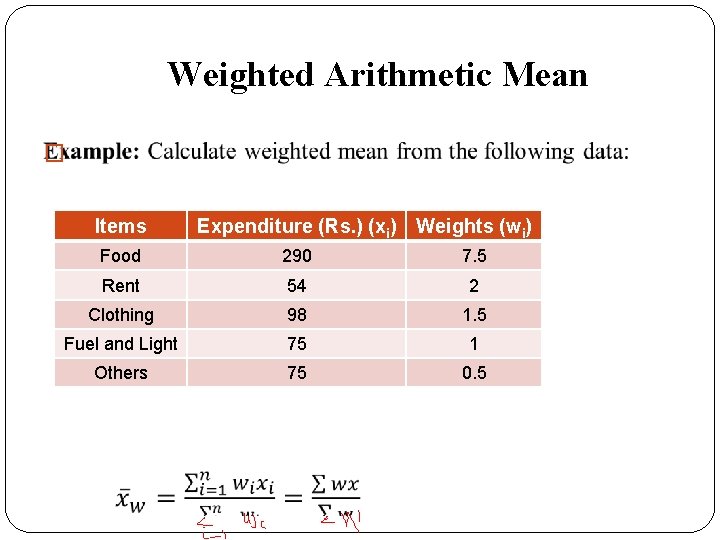
Weighted Arithmetic Mean �

Weighted Arithmetic Mean �

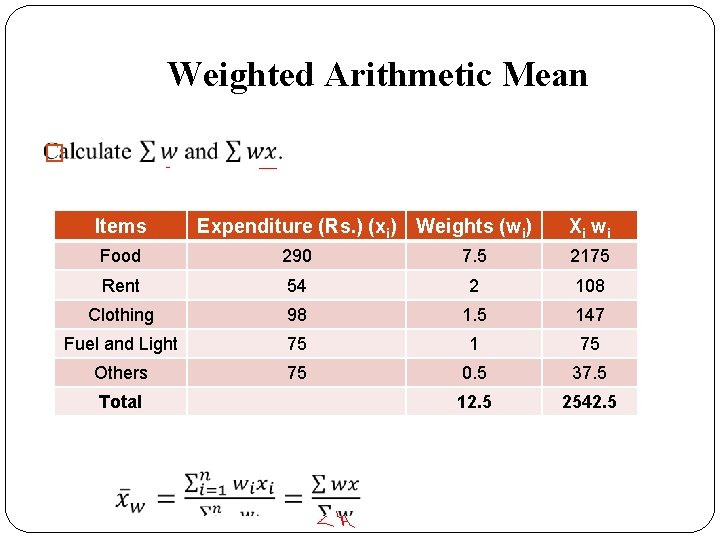
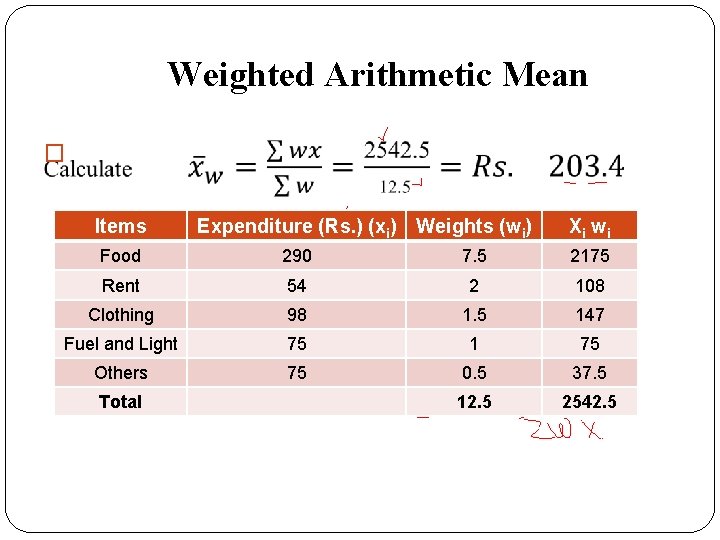
Weighted Arithmetic Mean � Items Expenditure (Rs. ) (xi) Weights (wi) Food 290 7. 5 Rent 54 2 Clothing 98 1. 5 Fuel and Light 75 1 Others 75 0. 5

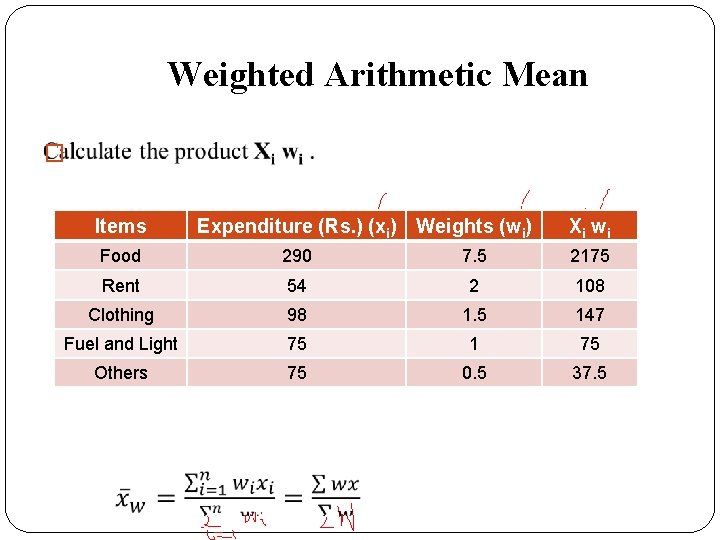
Weighted Arithmetic Mean � Items Expenditure (Rs. ) (xi) Weights (wi) Xi w i Food 290 7. 5 2175 Rent 54 2 108 Clothing 98 1. 5 147 Fuel and Light 75 1 75 Others 75 0. 5 37. 5

Weighted Arithmetic Mean � Items Expenditure (Rs. ) (xi) Weights (wi) Xi w i Food 290 7. 5 2175 Rent 54 2 108 Clothing 98 1. 5 147 Fuel and Light 75 1 75 Others 75 0. 5 37. 5 12. 5 2542. 5 Total

Weighted Arithmetic Mean � Items Expenditure (Rs. ) (xi) Weights (wi) Xi w i Food 290 7. 5 2175 Rent 54 2 108 Clothing 98 1. 5 147 Fuel and Light 75 1 75 Others 75 0. 5 37. 5 12. 5 2542. 5 Total

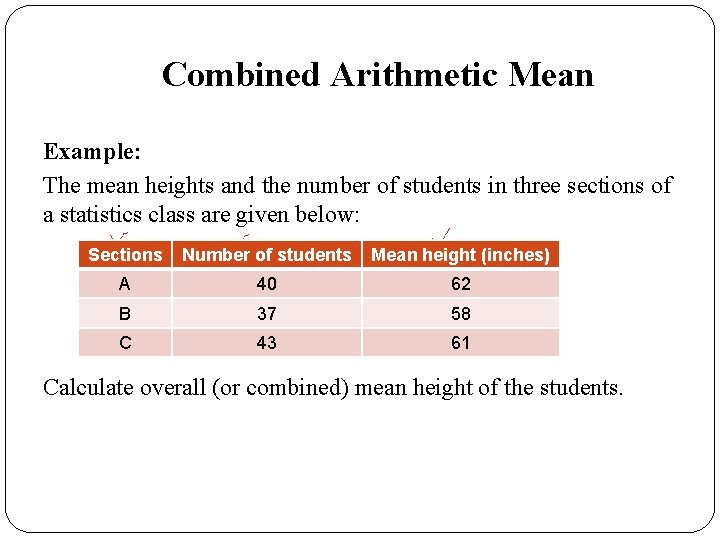
Combined Arithmetic Mean �

Combined Arithmetic Mean Example: The mean heights and the number of students in three sections of a statistics class are given below: Sections Number of students Mean height (inches) A 40 62 B 37 58 C 43 61 Calculate overall (or combined) mean height of the students.

Combined Arithmetic Mean � Sections Number of students Mean height (inches) A 40 62 B 37 58 C 43 61

Merits of Arithmetic Mean are: � Easy to calculate and understand. � Based on all observations. � Can be expressed by a mathematical formula.

De-Merits of Arithmetic Mean are: � It is greatly affected by extreme values. Example: Mean of 1, 2, 3, 4 and 5 is 3. If we change last number 5 to 20 then mean is 6. Note that 6 is not a representative number as most of the data in this case is below the average (i. e. 6). � Works well only in case of symmetric distributions and performs poorly in case of skewed distributions.

De-Merits of Arithmetic Mean are: � Bipolar case misrepresented (e. g. 50% of the students in a class got full marks and remaining 50% got zero marks). � If the grouped data has ‘open-end’ classes, then mean can not be calculated without assuming the limits.

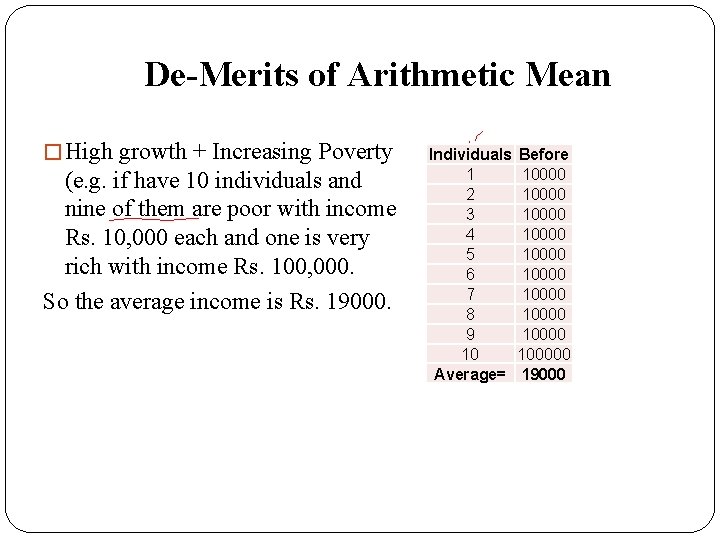
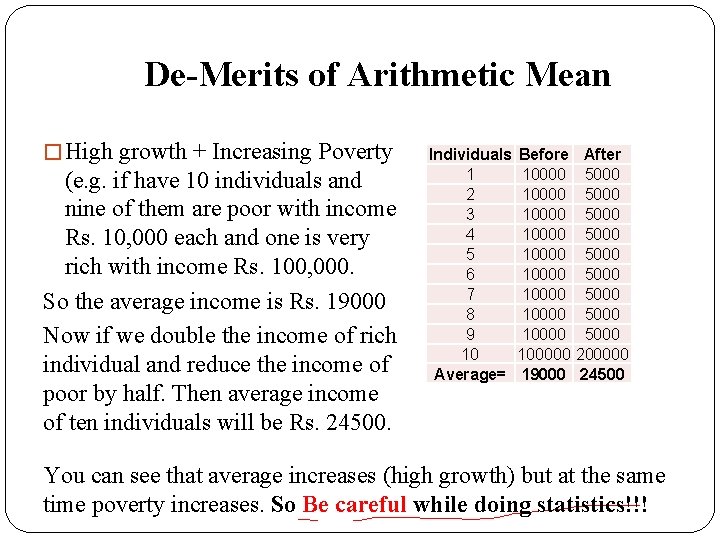
De-Merits of Arithmetic Mean � High growth + Increasing Poverty (e. g. if have 10 individuals and nine of them are poor with income Rs. 10, 000 each and one is very rich with income Rs. 100, 000. So the average income is Rs. 19000. Individuals 1 2 3 4 5 6 7 8 9 10 Average= Before 10000 10000 100000 19000

De-Merits of Arithmetic Mean � High growth + Increasing Poverty (e. g. if have 10 individuals and nine of them are poor with income Rs. 10, 000 each and one is very rich with income Rs. 100, 000. So the average income is Rs. 19000. Now if we double the income of rich individual and reduce the income of poor by half. Then average income of ten individuals will be Rs. 24500. Individuals 1 2 3 4 5 6 7 8 9 10 Average= Before 10000 10000 100000 19000 After 5000 5000 5000 200000 24500

De-Merits of Arithmetic Mean � High growth + Increasing Poverty (e. g. if have 10 individuals and nine of them are poor with income Rs. 10, 000 each and one is very rich with income Rs. 100, 000. So the average income is Rs. 19000 Now if we double the income of rich individual and reduce the income of poor by half. Then average income of ten individuals will be Rs. 24500. Individuals 1 2 3 4 5 6 7 8 9 10 Average= Before 10000 10000 100000 19000 After 5000 5000 5000 200000 24500 You can see that average increases (high growth) but at the same time poverty increases. So Be careful while doing statistics!!!

Median divides the arranged data (either ascending or descending order) into two equal parts in such a way that 50% of the data lies before the median and the remaining 50% of the data lies above it.

Median for Ungrouped Data Computation: � Arrange the data in ascending order (smallest value to largest value). � Compute an index i=(n/2) where n is the number of observations. �If i is not an integer, round up. The next integer greater than i denotes the position of the Median. �If i is an integer, then Median is the average of the values in positions i and i+1.

Median for Ungrouped Data Example: Marks obtained by 5 students, 20, 15, 3, 25, 10 Solution: � Arrange the data in ascending order. 3, 10, 15, 20, 25 � Compute an index i=(n/2) where n=5 is the number of observations. i=(n/2)=5/2=2. 5 Since i=2. 5 is not an integer, so the next integer greater than 2. 5 is 3, which gives the position of the Median. At third position, we have number 15. Hence Median=15

Median for Ungrouped Data Example: Run made by a cricket player in 4 matches: 30, 70, 10, 20 Solution: � Arrange the data in ascending order. 10, 20, 30, 70 � Compute an index i=(n/2) where n=4 is the number of observations. i=(4/2)=2 Since i=2 is an integer, so Median is the average of the values in positions i and i+1. i. e. Median is the average of the values in positions 2 and 3. At position 2, we have number 20. At position 3, we have number 30. Hence Median=average of 20 and 30= (20+30)/2=50/2=25

Review Let’s review the main concepts: Measures of Central Tendency �Weighted Mean �Combined Mean �Merits and demerits of Arithmetic Mean � Median 23

Next Lecture In next lecture, we will study: Measures of Central Tendency � Median �Median for grouped Data �Merits and demerits of Median � Mode �Mode for Grouped Data �Mode for Ungrouped Data �Merits and demerits of Mode 24

Next Lecture In next lecture, we will study: Measures of Central Tendency � Geometric Mean �Geometric Mean for Grouped Data �Geometric Mean for Ungrouped Data �Merits and demerits of Geometric Mean 25