MTA Sz TAKI Veszprm University Hungary Guests at

MTA Sz. TAKI & Veszprém University (Hungary) Guests at INRIA, Sophia Antipolis, 2000 and 2001 Paintbrush Rendering of Images Tamás Szirányi

Stochastic Paintbrush Rendering u Stochastic relaxation method to generate images (based on a reference image) by simulating a simple painting method, u Sharp contours, well-defined segmentation areas, elaborated fine details, u A priori models or interactions are not needed. 2

Painted image with raw strokes Visible contours of strokes 3

Objectives u. Stochastic painting method u. Need for optimization u. MCMC optimization u. MRF and PB for segmentation 4

Result of an impressionist-like process controlled by an edge map (P. Litwinowicz, “Processing Images and Video for An Impressionist Effect”, Computer Graphics, Proc. SIGGRAPH’ 1997, 1997. ) 5

Paintings of A. Dürer and M. Munkácsy, representing careful life-style painting: the painter tries to elaborate the painting without visible effects of the brush-strokes 6

7

8

9

10

Painting following a real-life picture 11

Painting, following a real-life picture 12

Painting following an artist`s painting 13

Painting following an artist`s painting 14

Painting following an artist`s painting 15

Painting repairing JPEG 16

Painting following an artist`s painting 17

18

Segmentation Original with edge-map 19

Painted (stroke is 37*9) and its edge 20

Painted (stroke is 10*3) and its edge 21

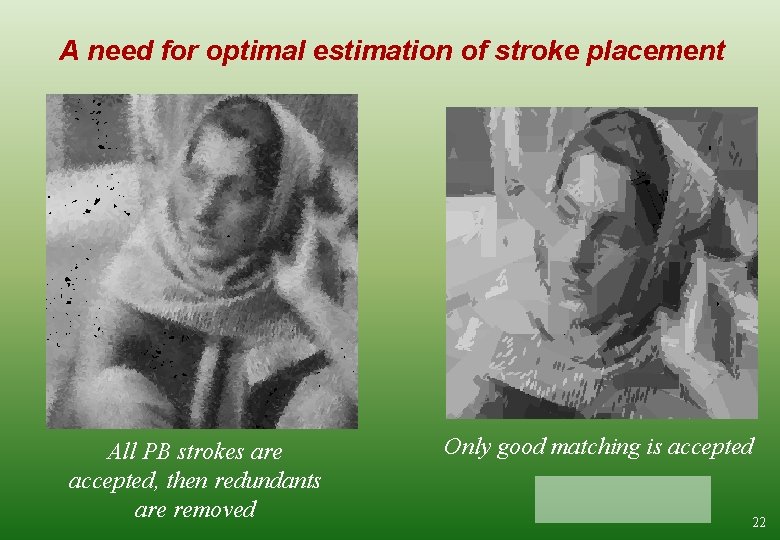
A need for optimal estimation of stroke placement All PB strokes are accepted, then redundants are removed Only good matching is accepted 22

Markov Chain Monte Carlo (MCMC) methods Ergodic Markov-chain (X 1, X 2, …. Xn) Stationary f(X) Sample series (X 1, X 2, …. Xn) generated with target density f(X) Paintbrush strokes: X is the position of a stroke, f(X) is the probability density of distortion error between the stroke and the reference image at position X 23

Metropolis-Hastings algorithm 24

Independent MH 25

Random Walk MH 26

Probability densities of distortion error of the proposed ( Yt) and accepted (X t+1=Yt) strokes versus the original image when generating the strokes for ‘Barbara’ image. First, coarse (20 x 5), finally, fine (7 x 2) strokes are generated 27

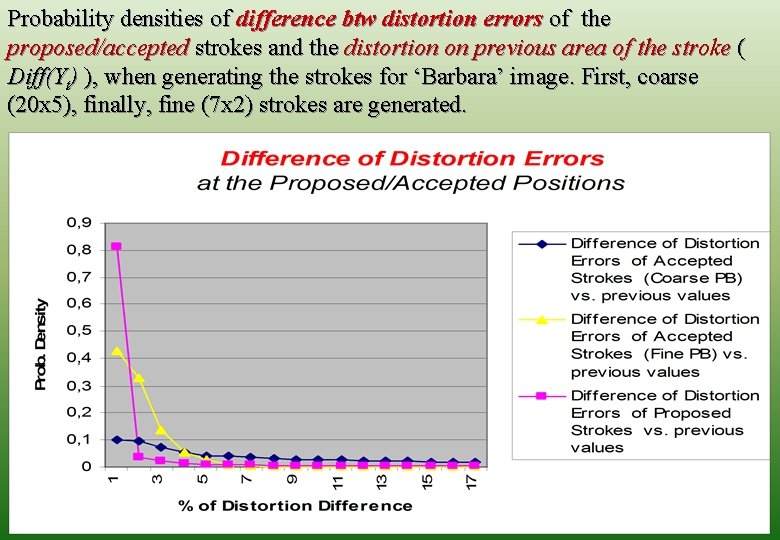
Probability densities of difference btw distortion errors of the proposed/accepted strokes and the distortion on previous area of the stroke ( Diff(Yt) ), when generating the strokes for ‘Barbara’ image. First, coarse (20 x 5), finally, fine (7 x 2) strokes are generated. 28

The characteristic variable is the Difference of distortion error instead of the error 29

accept/reject rule 30

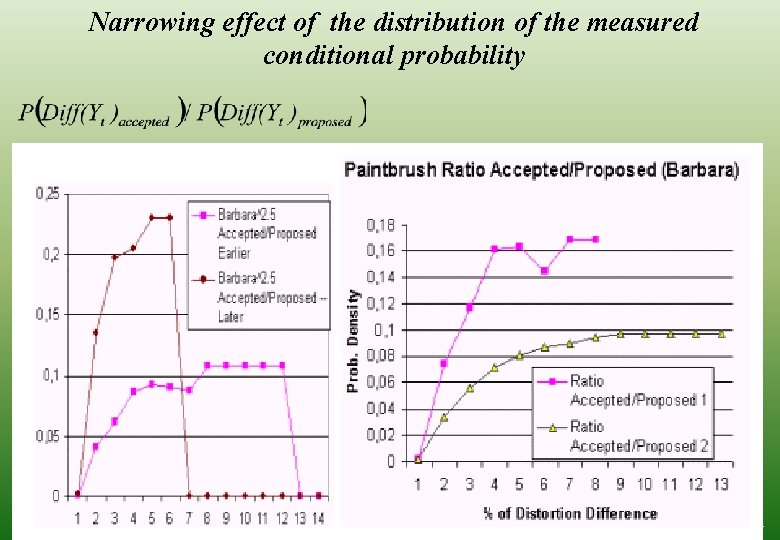
Narrowing effect of the distribution of the measured conditional probability 31

Constraints for the flexible accept/reject rule 32

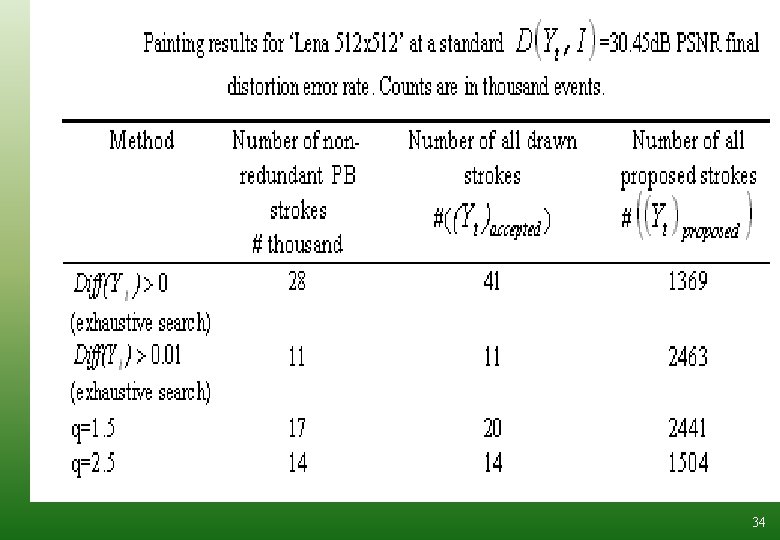
Method Number of nonredundant PB strokes # thousand Number of all drawn strokes # Number of all proposed strokes # Random Stochastic search 35 61 2645 Metropolis Hastings process 26 31 1555 33

34

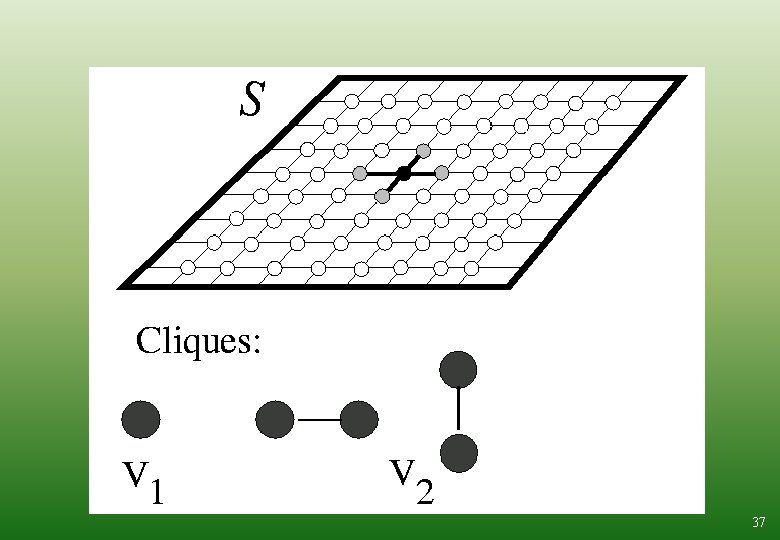
Connection btw MRF segmentation and PB Limiting the number of colors Coupling the neighboring strokes Reference area is greater than the stroke’s area MRF-like segmentation Halftone effects by strokes (modulation) 35

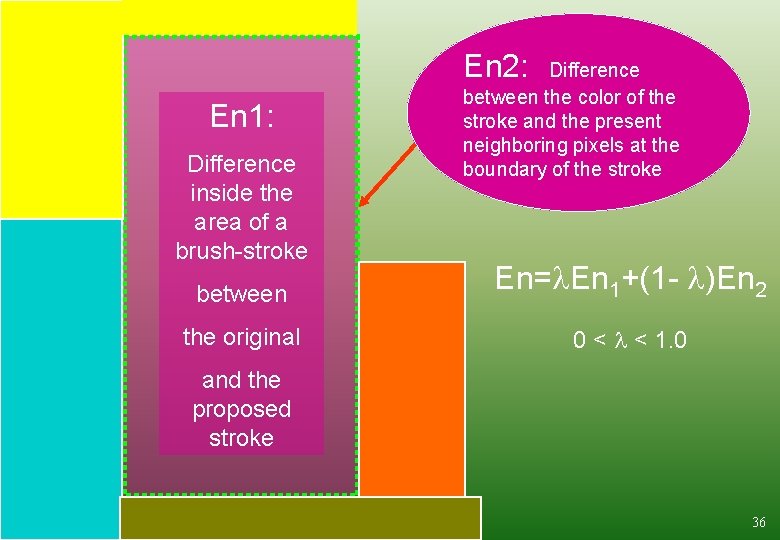
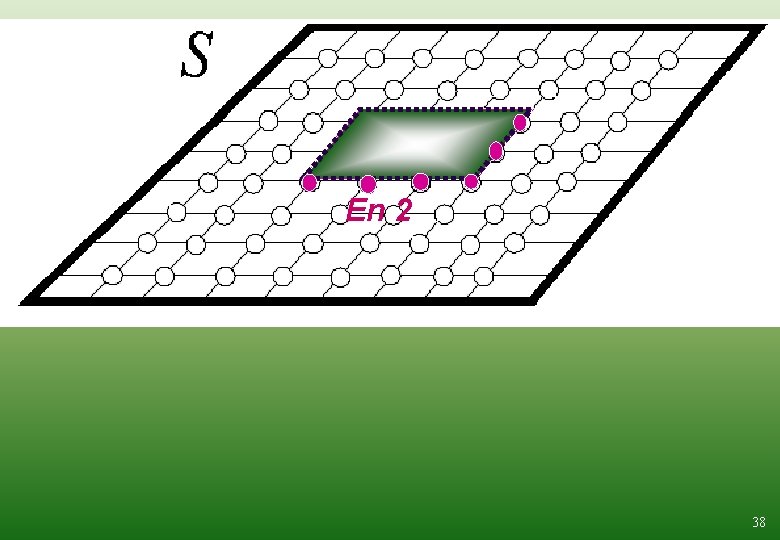
En 2: En 1: Difference inside the area of a brush-stroke Difference between the color of the stroke and the present neighboring pixels at the boundary of the stroke between En= En 1+(1 - )En 2 the original 0 < < 1. 0 and the proposed stroke 36

37

En 1 En 2 38

39

Noisy input Painting ( = 0. 6, No. Co. = 30 ) Painting En < 0 MMD 40

41

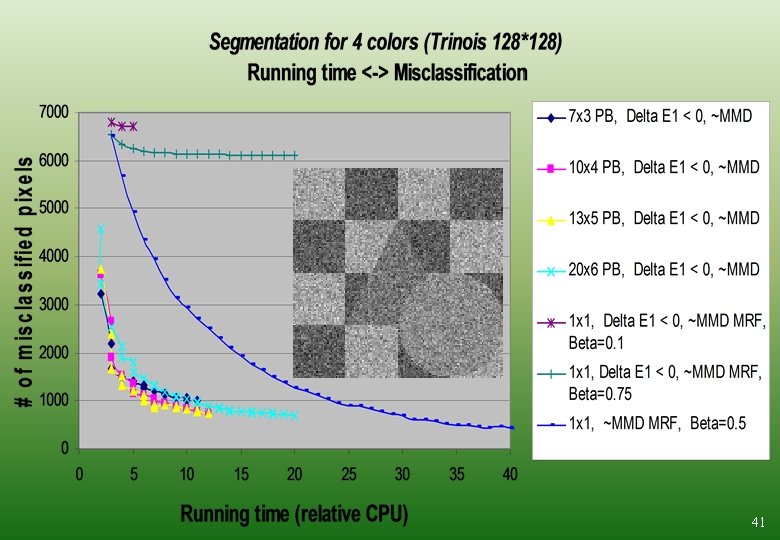
7*3 PB 13*5 PB 20*6 PB E 1 < 0, ~MMD MRF 42

Motion-Field u Gradient and block-matching motion fields Gradient-based Block-matching 43

Examples 1/2 1. 2. transformed video Edge map of transformed video 3. 44

Example 2/2 a frame 1: keyframe 1 frame 2: painted motion area frame 3: 1 painted motion ar • 1. and 5. are keyframes frame 4: painted motion area 3 frame 5: keyframe 2 45

Example 2/2 b frame 1: keyframe 1 frame 2: painted motion area frame 3: 1 painted motion area frame 4: painted motion area 3 frame 5: keyframe 2 46

Comparison Original Cinepak 47

23 Comparison u With Cinepak-codec Cinepak PB result 48

Thank you for the attention 49

Appendix 50

Segmentation by painting, when distortion error may increase 51

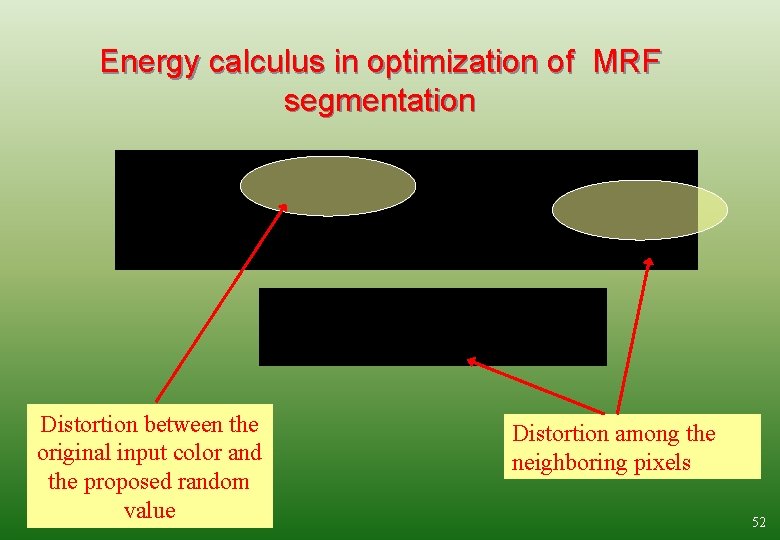
Energy calculus in optimization of MRF segmentation Distortion between the original input color and the proposed random value Distortion among the neighboring pixels 52

Independent MH Since the probability of acceptance of Yt depends on X(t), the resulting sample is not independent and identically distributed (iid). X(t) is irreducible and aperiodic (thus ergodic) iff g is almost everywhere positive on the support of f. The above algorithm produces a uniformly ergodic chain if there exists a constant M such that 53

Random Walk MH RW-MH does not enjoy uniform ergodicity properties, but there are necessary and sufficient conditions for geometric ergodicity, e. g. the logconcave case, when 54