MT144 NETWORK ANALYSIS Mechatronics Engineering 13 1 Sinusoids

MT-144 NETWORK ANALYSIS Mechatronics Engineering (13) 1

Sinusoids and Phasors

Contents • • Introduction Sinusoids Phasor Relationships for Circuit Elements Impedance and Admittance Kirchhoff’s Laws in the Frequency Domain Impedance Combinations Applications

Introduction • AC is more efficient and economical to transmit power over long distance. • A sinusoid is a signal that has the form of the sine or cosine function. • Circuits driven by sinusoidal current (ac) or voltage sources are called ac circuits. • Why sinusoid is important in circuit analysis? – Nature itself is characteristically sinusoidal. – A sinusoidal signal is easy to generate and transmit. – Easy to handle mathematically

Sinusoids

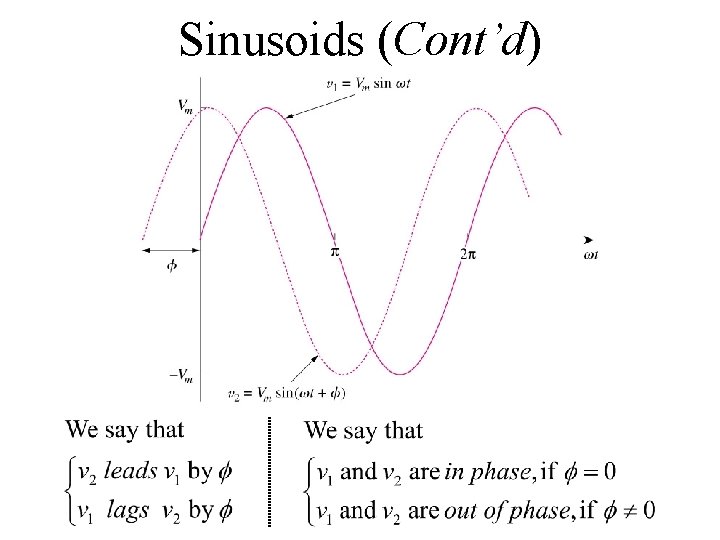
Sinusoids (Cont’d) • A period function is one that satisfies f(t) = f(t+n. T), for all t and for all integers n. – The period T is the number of seconds per cycle – The cyclic frequency f = 1/T is the number of cycles per second

Sinusoids (Cont’d)

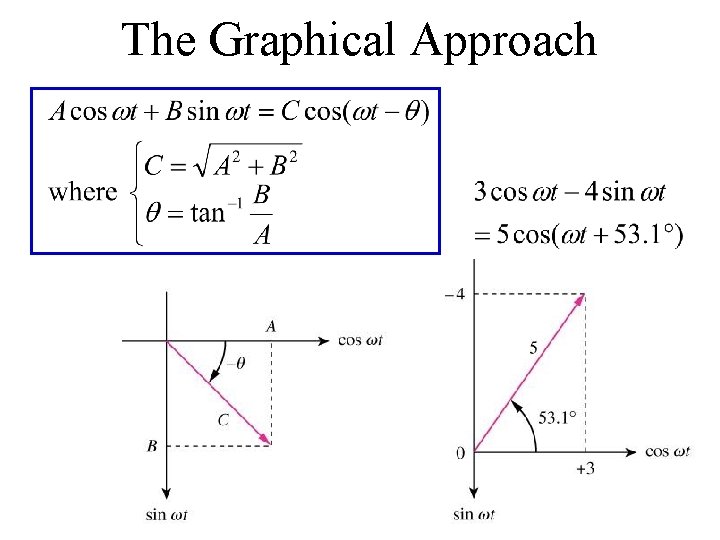
Sinusoids (Cont’d) • To compare sinusoids – Use the trigonometric identities – Use the graphical approach

The Graphical Approach

Phasors • Sinusoids are easily expressed by using phasors • A phasor is a complex number that represents the amplitude and the phase of a sinusoid. • Phasors provide a simple means of analyzing linear circuits excited by sinusoidal sources.

Phasors (Cont’d)

Important Mathematical Properties

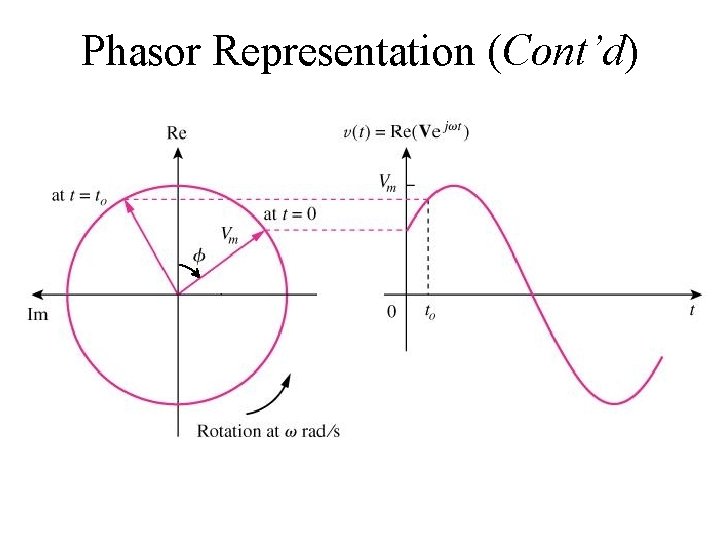
Phasor Representation

Phasor Representation (Cont’d)

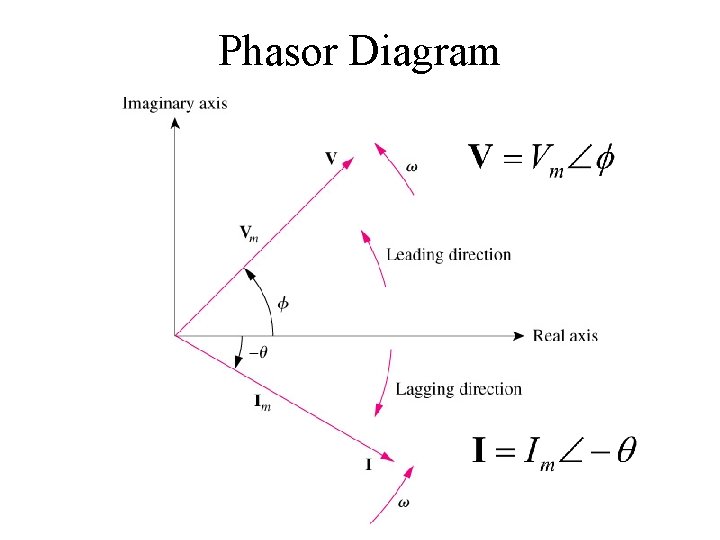
Phasor Diagram

Sinusoid-Phasor Transformation

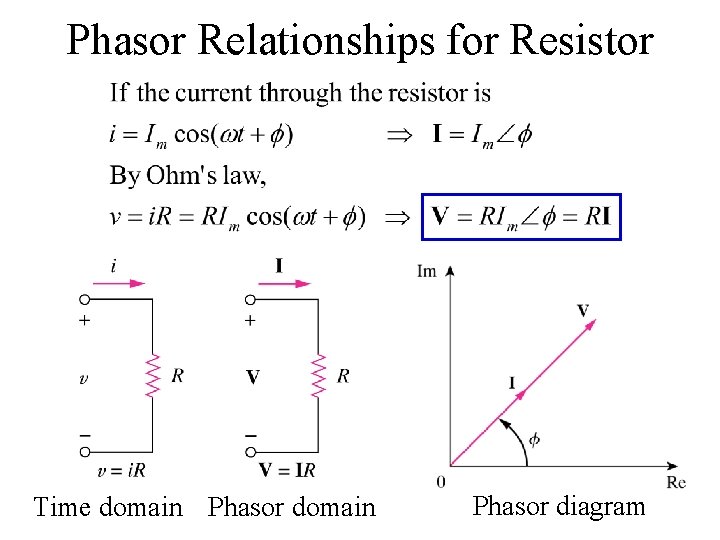
Phasor Relationships for Resistor Time domain Phasor diagram

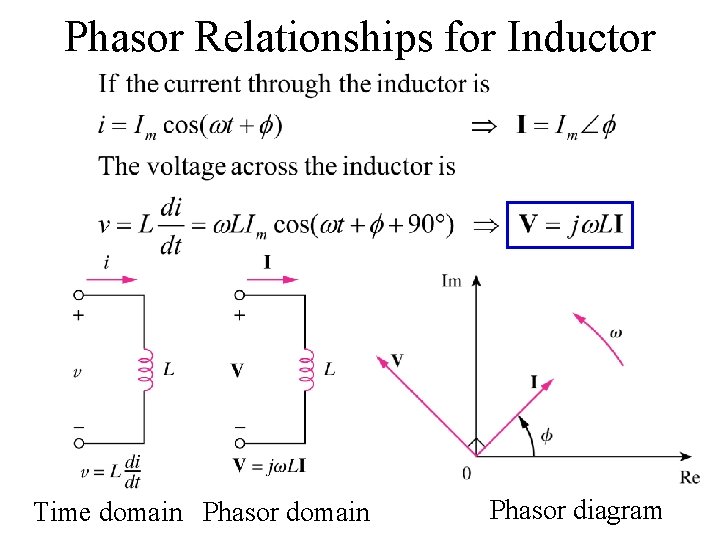
Phasor Relationships for Inductor Time domain Phasor diagram

Phasor Relationships for Capacitor Time domain Phasor diagram

Impedance and Admittance

Impedance and Admittance (Cont’d)

Impedance and Admittance (Cont’d)

Impedance and Admittance (Cont’d)

KVL and KCL in the Phasor Domain

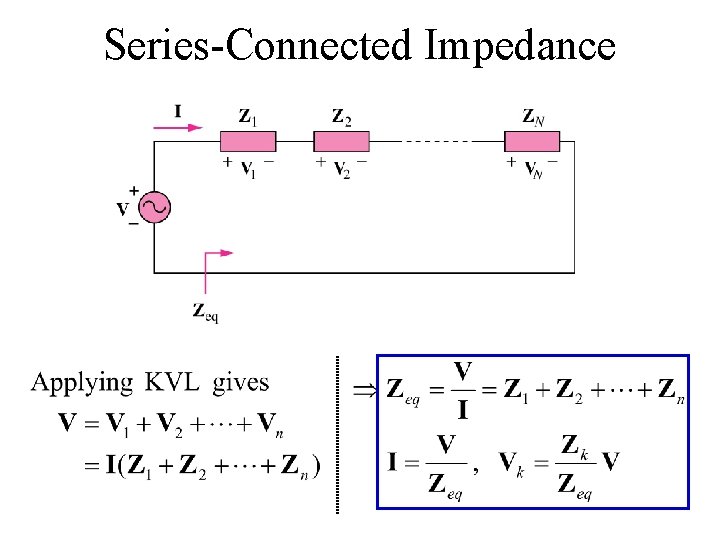
Series-Connected Impedance

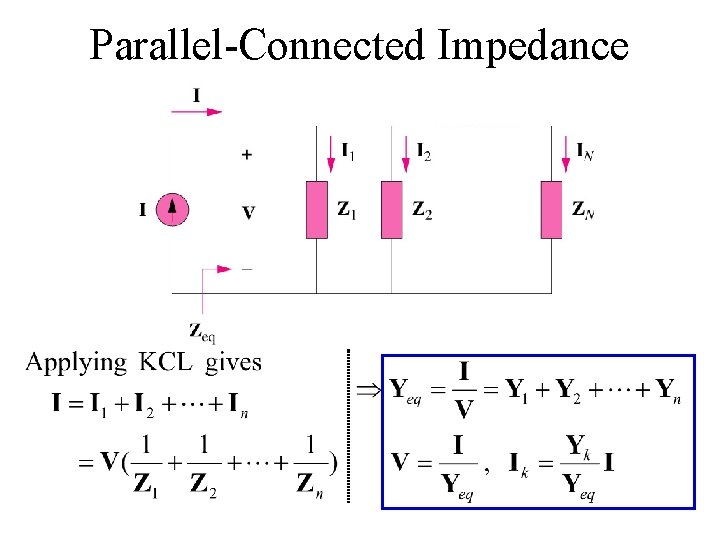
Parallel-Connected Impedance

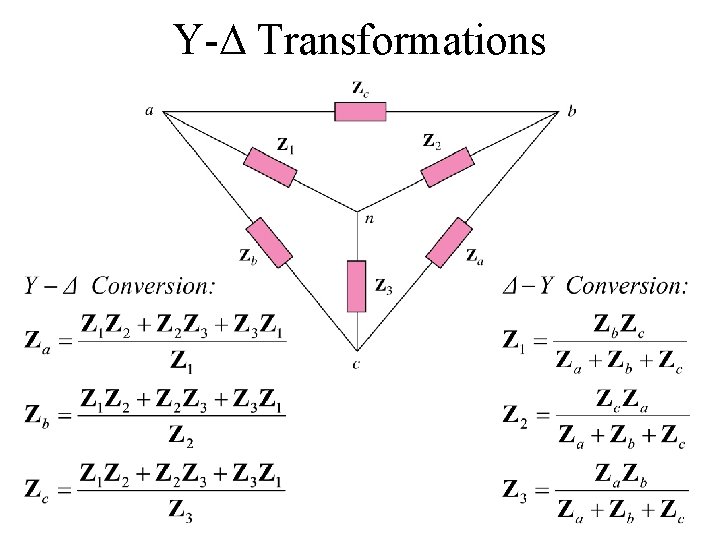
Y- Transformations

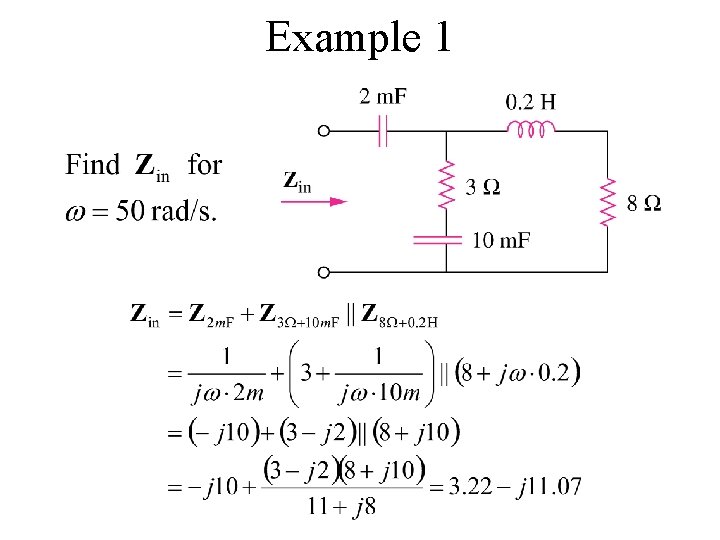
Example 1

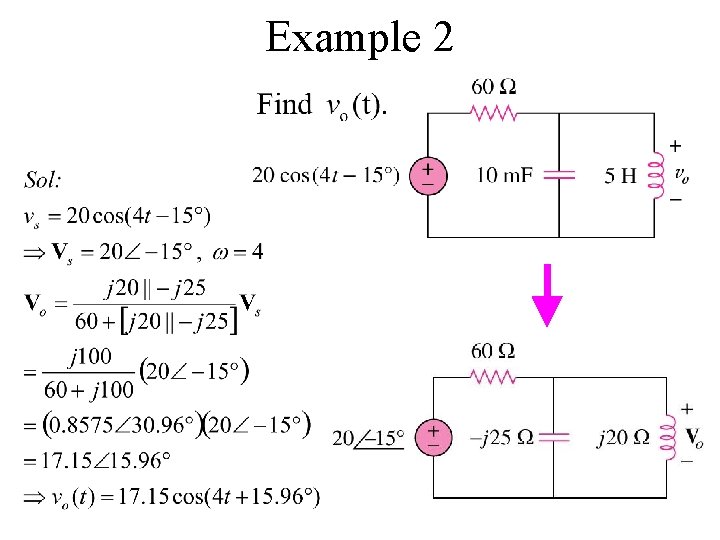
Example 2

Example 3 -Y transformation

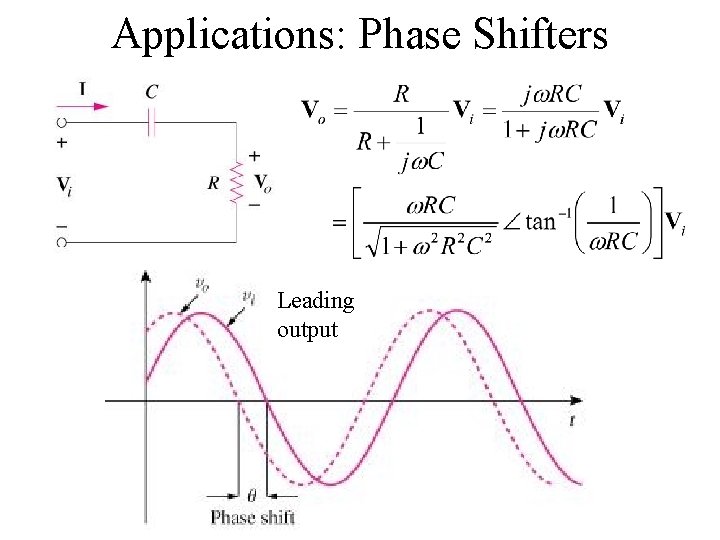
Applications: Phase Shifters Leading output

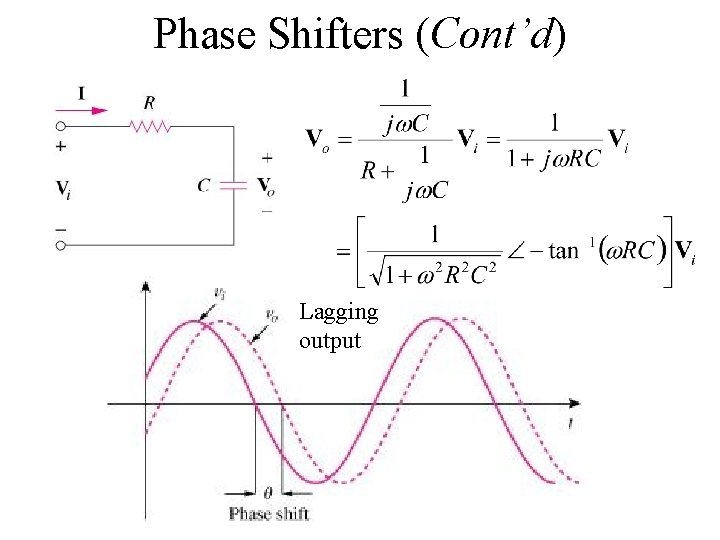
Phase Shifters (Cont’d) Lagging output

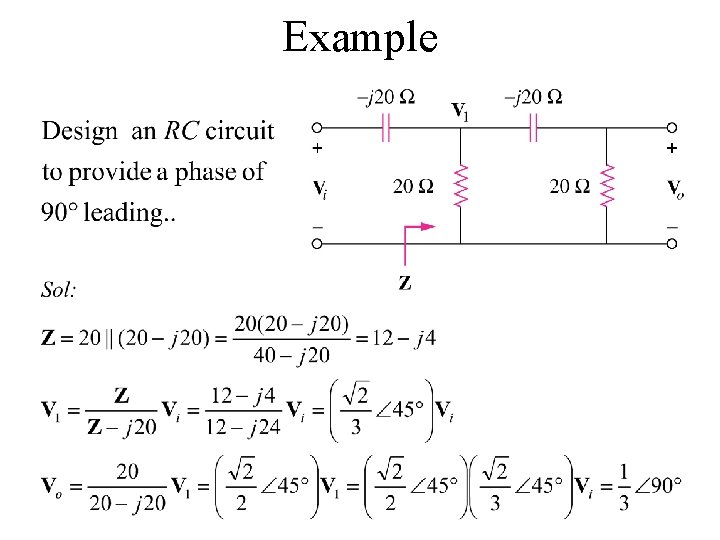
Example

Applications: AC Bridges

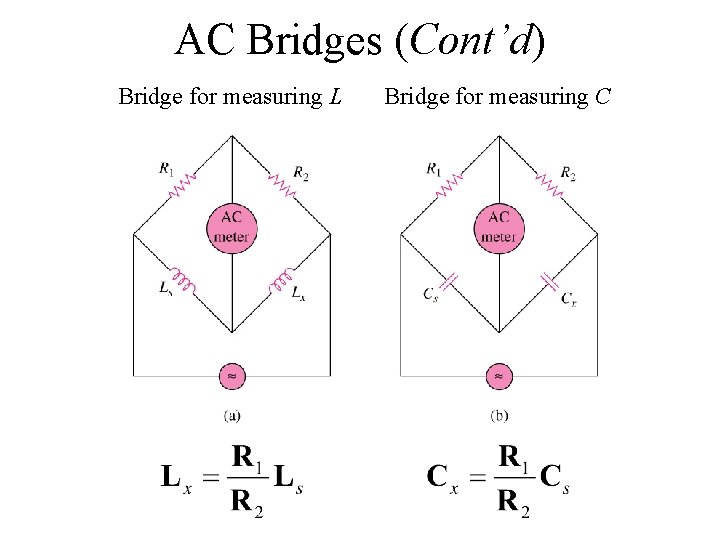
AC Bridges (Cont’d) Bridge for measuring L Bridge for measuring C

Summary • Transformation between sinusoid and phasor is given as • Impedance Z for R, L, and C are given as • Basic circuit laws apply to ac circuits in the same manner as they do for dc circuits.