MSE 348 The LShaped Method Theory and Example

MS&E 348 The L-Shaped Method: Theory and Example 2/5/04 Lecture

Review: Dantzig-Wolfe (“DW”) Decomposition • We recognize delayed column generation as the centerpiece of the decomposition algorithm • Even though the master problem can have a huge number of columns, a column is generated only after it is found to have a negative reduced cost and is about to enter the basis • The subproblems are smaller LP problems that are employed as an economical search method for discovering columns with negative reduced costs • A variant can be used whereby all columns that have been generated in the past are retained

Review: Benders Decomposition • Benders decomposition uses delayed constraint generation and the cutting plane method, and should be contrasted with DW that uses column generation • Benders is essentially the same as DW applied to the dual • Similarly as for DW, we have the option of discarding all or some of the constraints in the relaxed primal that have become inactive

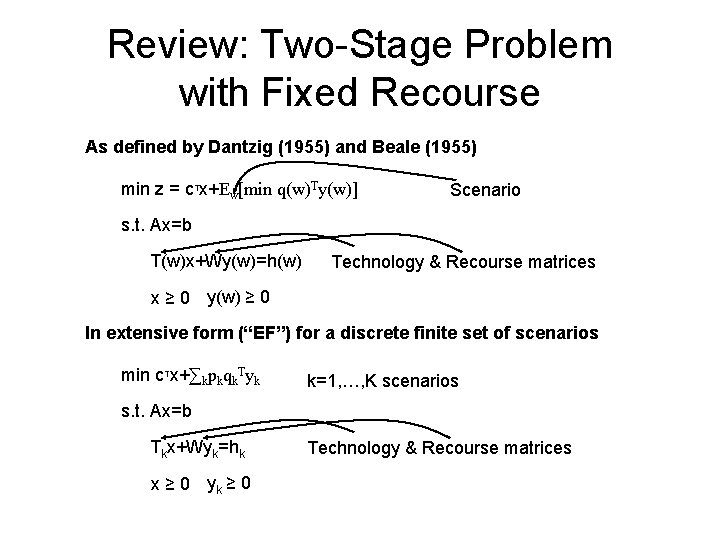
Review: Two-Stage Problem with Fixed Recourse As defined by Dantzig (1955) and Beale (1955) min z = c. Tx+Ew[min q(w)Ty(w)] Scenario s. t. Ax=b T(w)x+Wy(w)=h(w) Technology & Recourse matrices x ≥ 0 y(w) ≥ 0 In extensive form (“EF”) for a discrete finite set of scenarios min c. Tx+∑kpkqk. Tyk k=1, …, K scenarios s. t. Ax=b Tkx+Wyk=hk x ≥ 0 yk ≥ 0 Technology & Recourse matrices

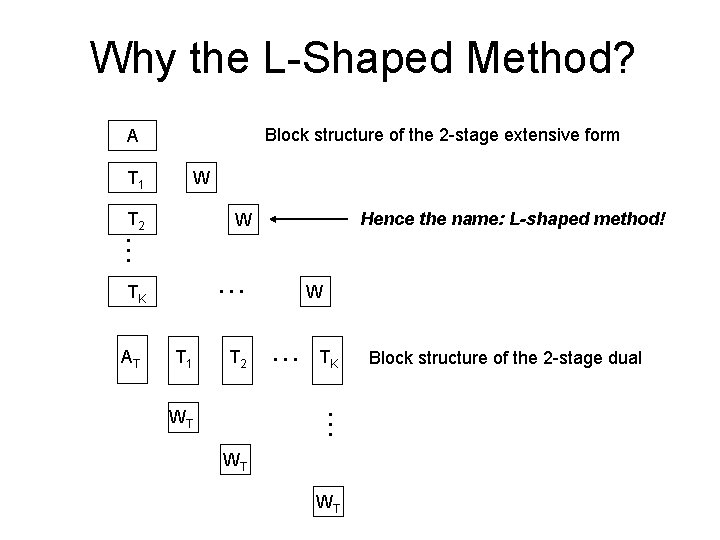
Why the L-Shaped Method? Block structure of the 2 -stage extensive form A T 1 W T 2 … … TK AT Hence the name: L-shaped method! W T 1 T 2 … TK … WT WT Block structure of the 2 -stage dual

Connection between Benders/DW and the L-Shaped Method • Given this block structure, it seems natural to exploit the dual structure by performing a DW (1960) decomposition (inner linearization) of the dual • … or a Benders (1962) decomposition (outer linearization) of the primal • The method has been extended in stochastic programming to take care of feasibility questions and is known as Van Slyke and Wets’ (1969) Lshaped method • It is a cutting plane technique

Comments on the L-Shaped Method - The method consists of solving an approximation of the recourse function by using an outer linearization of Q. Two types of constraints are sequentially added: (i) feasibility cuts determining { x | Q(x) < +∞} and (ii) optimality cuts that are linear approximations to Q on its domain of finiteness - Observe that solving P 1 is equivalent to solving P 2 P 1: min c. T x + Q(x) P 2: min c. T x + Ө s. t. x Є K 1 ∩ K 2 Q(x) ≤ Ө K 1 = { x | Ax=b, x≥ 0 } K 2 = { x | Q(x) < ∞ } s. t. x Є K 1 ∩ K 2

The L-Shaped Algorithm Step 0. Set r = s = v = 0 (these are indices initially set at zero) Step 1. Set v = v+1 (v is the iteration index) and solve the LP (1) - (3) min z = c. Tx + Ө (1) s. t. Ax=b Dlx ≥ dl l=1, …, r feasibility cuts (2) Gs x + Ө ≥ gs l=1, …, s optimality cuts (3) x ≥ 0 and Ө is a free real number Let (xv, Өv) be an optimal solution. Detail for Initialization: if no constraint (3) is present, Өv is set equal to -∞ and is not considered in the computation of xv.

The L-Shaped Algorithm (Cont’d) Step 2. For k = 1, …, K solve the LP (Phase I Simplex) ∆!: these are obviously ≠ min wk’ = e. Tu+ + e. Tus. t. W y + I u+- I u- = hk - Tk xv (4) Identity matrix (5) y ≥ 0, u+ ≥ 0, u- ≥ 0 where e. T = (1, … , 1) until for some k, the optimal value wk’ > 0 In this case, let σv be the associated simplex multipliers and define (6) Dr+1= (σv)T Tk and dr+1 = (σv)T hk (7) to generate a feasibility cut of type (2). Set r = r + 1, add to the constraint set (2), and return to Step 1. If for all k, wk’ = 0, go to step 3

The L-Shaped Algorithm (Cont’d) Step 3. For k = 1, …, K solve the LP min wk = qk. T y s. t. W y = hk - Tk xv y≥ 0 (8) Let Πkv be the simplex multipliers associated with the optimal solution of problem k of type (8). Define Gs+1= ∑kpk (Πkv)T Tk (9) gs+1= ∑kpk (Πkv)T hk (10) and Let wv = gs+1 – Gs+1 xv If Өv ≥ wv, stop as xv is an optimal solution. Otherwise, set s = s + 1, add to the constraint set (3) and return to Step 1.

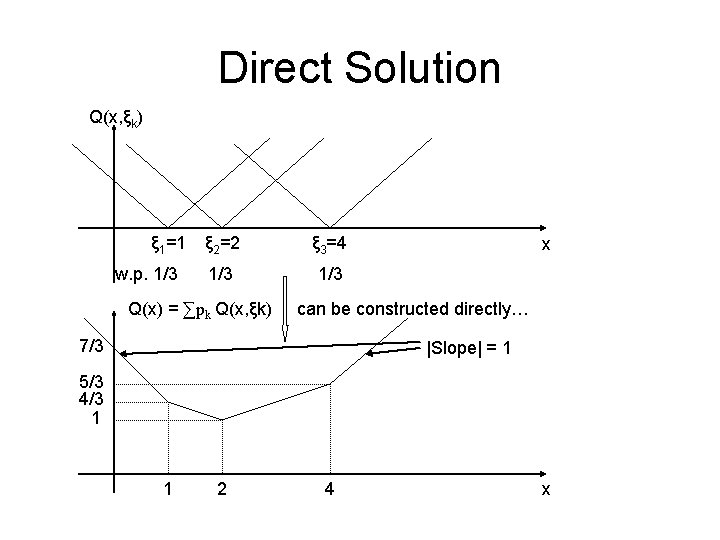
Example min z = 0 + Q(x, ξk) (we assume c. T = 0) where Q(x, ξ) = ξ - x if x ≤ ξ x - ξ if x ≥ ξ We also assume 0 ≤ x ≤ 10 1 w. p. 1/3 and ξ= 2 w. p. 1/3 4 w. p. 1/3 Solve this example : (i) directly (ii) by using the L-shaped algorithm

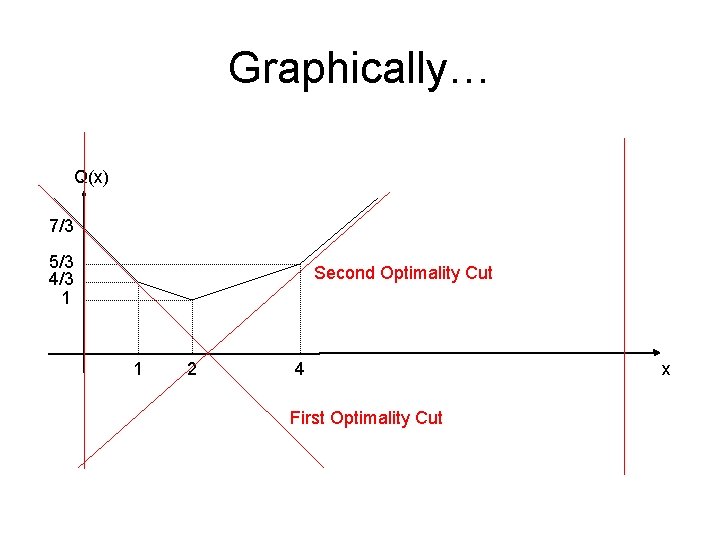
Direct Solution Q(x, ξk) ξ 1=1 w. p. 1/3 ξ 2=2 ξ 3=4 1/3 Q(x) = ∑pk Q(x, ξk) x can be constructed directly… 7/3 |Slope| = 1 5/3 4/3 1 1 2 4 x

Using the L-Shaped Algorithm - There are no feasibility cuts as K 1 = R (there is no Ax=b constraint) and K 2 = R (Q(x) is defined everywhere) -We can reformulate this problem to fit the notation previously used Each subproblem can be formulated as: min y 1 s. t. y 1 – y 2 = ξ -x y 1 – y 3 = - ξ + x which is equivalent to… min wk = qk. T y s. t. W y = hk - Tk xv with W = y≥ 0 ξ 1 1 -1 0 , hk = , Tk = -ξ -1 1 0 -1

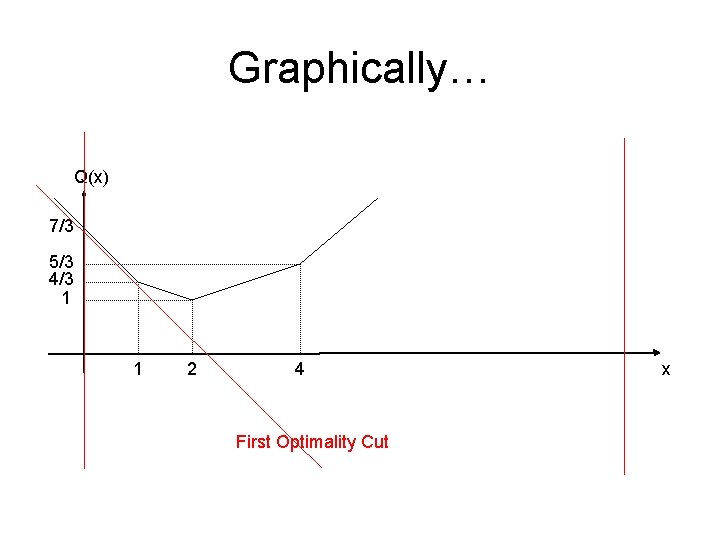
Iteration by Iteration 1 We solve min Ө s. t. 0 ≤ x ≤ 10 Since at initialization, we assume Ө 1 = -∞ Since x is undetermined, we assume we start at x 1=0 There’s no feasibility issue, we go to Step 3 of the algorithm We find G 1 = ∑k ⅓ [1 0] g 1 = ∑k ⅓ [1 0] 1 =1 -1 ξk = 7/3 -ξk Simplex multipliers are the same for all three scenarios… w 1 = g 1 – G 1 x 1 = 1 and w 1 > Ө 1 and (x 1 = 0, Ө 1 = -∞) is not optimal We add the cut of type (3): Ө ≥ 7/3 - x

Graphically… Q(x) 7/3 5/3 4/3 1 1 2 4 First Optimality Cut x

Iteration by Iteration (Cont’d) Iteration 2 We solve min Ө s. t. Ө ≥ 7/3 – x 0 ≤ x ≤ 10 We find (x 2 = 10, Ө 2 = -23/3) There’s no feasibility issue, we go to Step 3 of the algorithm We find G 2 = ∑k ⅓ [0 1] g 2 = ∑k ⅓ [0 1] 1 = -1 -1 ξk = -7/3 -ξk Simplex multipliers are the same for all three scenarios… w 2 = g 2 – G 2 x 2 = 23/3 and w 2 > Ө 2 and (x 2 = 10, Ө 2 = -23/3) is not optimal We add the optimality cut: Ө ≥ x – 7/3

Graphically… Q(x) 7/3 5/3 4/3 1 Second Optimality Cut 1 2 4 First Optimality Cut x

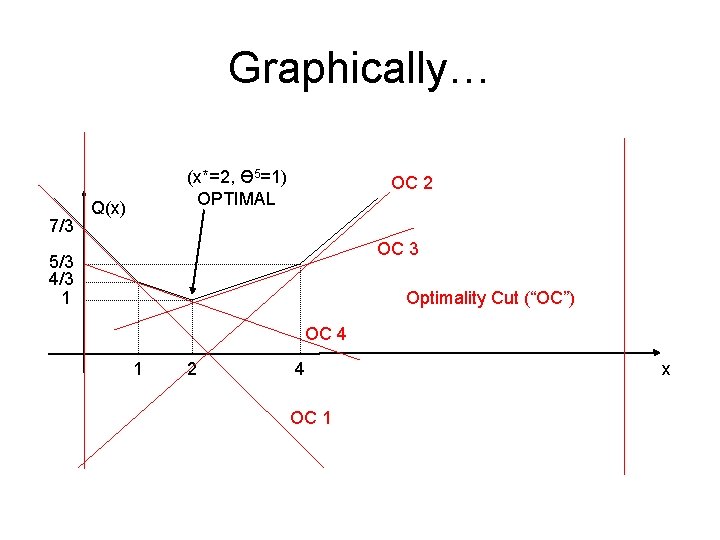
Iteration by Iteration (Cont’d) Iteration 3 We solve min Ө s. t. Ө ≥ 7/3 – x Ө ≥ x - 7/3 0 ≤ x ≤ 10 We find (x 3 = 7/3, Ө 3 = 0) We find G 3 = ⅓ [0 1] Simplex multipliers are NOT the same for all three scenarios… 1 + ⅓ [0 1] 1 + ⅓ [1 0] 1 = -1/3 -1 -1 -1 g 3 = 1/3 w 3 = g 3 – G 3 x 3 = 10/9 and w 3 > Ө 3 and (x 3 = 7/3, Ө 3 = 0) is not optimal We add the optimality cut: Ө ≥ (x+1)/3

Iteration by Iteration (Cont’d) Iteration 4 We find (x 4 = 3/2, Ө 4 = 5/6) which is not optimal We add the optimality cut: Ө ≥ (5 -x)/3 Iteration 5 We find (x 5 = 2, Ө 5 = 1) which is OPTIMAL

Graphically… 7/3 (x*=2, Ө 5=1) OPTIMAL Q(x) OC 2 OC 3 5/3 4/3 1 Optimality Cut (“OC”) OC 4 1 2 4 OC 1 x