MS Algebra AFIF7 Ch 7 1 Solve Linear
MS Algebra A-F-IF-7 – Ch. 7. 1 Solve Linear Systems by Graphing Mr. Deyo Solve Linear Systems by Graphing

Title: 7. 1 Solve Linear Systems by Graphing Date: Learning Target By the end of the period, I will solve linear systems by graphing. I will demonstrate this by completing Four. Square Notes and by solving problems in a pair/group activity.

Home Work 1 -2 -3: 2) Section 7. 1 Pg. 378 -381 Txt. Bk. Prob. #3, 5, 15, 23, 31, 35 Solved and Put in Binder? Date 1) Class 4 -Square Notes Put In Binder? 3) Section ______ Notes Copied on blank sheet of paper in Binder? Table of Contents Description Date Due
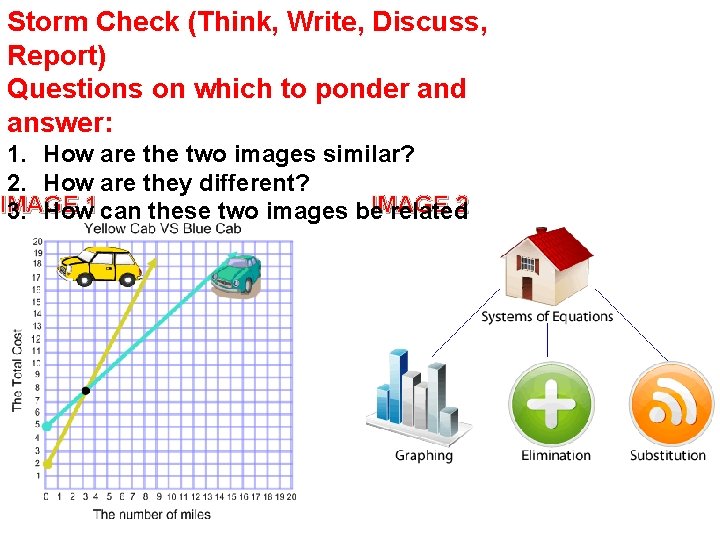
Storm Check (Think, Write, Discuss, Report) Questions on which to ponder and answer: 1. How are the two images similar? 2. How are they different? IMAGE 2 3. How 1 can these two images be related to math?
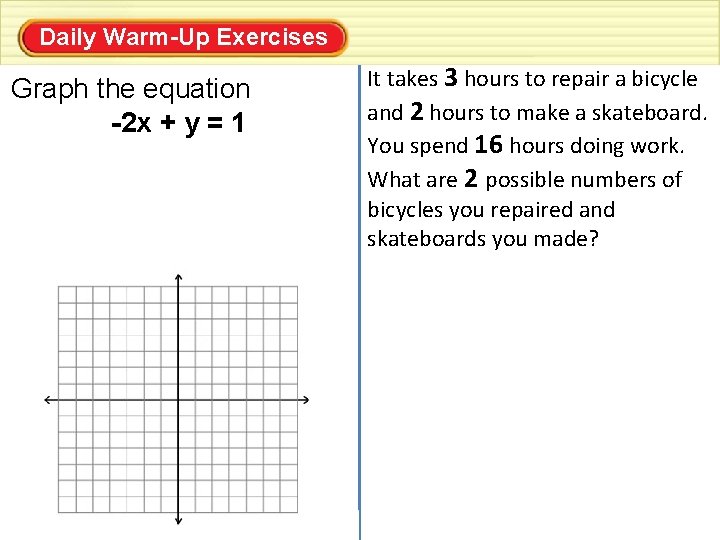
Daily Warm-Up Exercises For use with pages xxx–xxx Graph the equation -2 x + y = 1 It takes 3 hours to repair a bicycle and 2 hours to make a skateboard. You spend 16 hours doing work. What are 2 possible numbers of bicycles you repaired and skateboards you made?
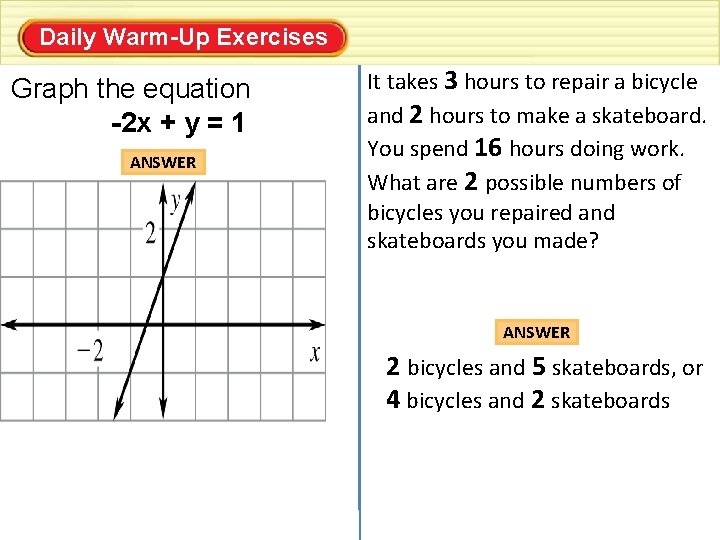
Daily Warm-Up Exercises For use with pages xxx–xxx Graph the equation -2 x + y = 1 ANSWER It takes 3 hours to repair a bicycle and 2 hours to make a skateboard. You spend 16 hours doing work. What are 2 possible numbers of bicycles you repaired and skateboards you made? ANSWER 2 bicycles and 5 skateboards, or 4 bicycles and 2 skateboards

Vocabulary 1) System of Linear Equations 2) Solution to a System of Equations 3) Solve by Graphing 4) Solve by Elimination 5) Solve by Substitution
Sketch DAY 2 1. Review word ¨Friendly Definition ¨Physical Representation 2. Draw a sketch Wordwork 1. 2. 3. 4. Word List DAY 3 and/or DAY 4 1. Review the word ¨Friendly Definition ¨Physical Representation 2. Show the word works ¨Synonyms/antonym ¨Word Problems ¨Related words/phrases ¨Example/non-example Friendly DAY Definition 1 1. Use Visuals 2. Introduce the word ¨Friendly Definition ¨Physical Representation 3. Use Cognates 4. Write friendly definition 5. Physical Representation Sentence DAY 5 1. Review the word ¨Friendly definition ¨Physical Representation 3. Write a sentence üat least 2 rich words (1 action) ücorrect spelling ücorrect punctuation ücorrect subject/predicate agreement üclear and clean writing

Notes: System of Linear Equations A system of equations (linear system) has two or more linear equations with the same variables. y = -x + 5 Equation 2: y = ½ x + 2 Equation 1: A solution to the system is an ordered pair ( x, y ) that is a solution to EACH of the equations (where the lines intersect). solution (2, 3)
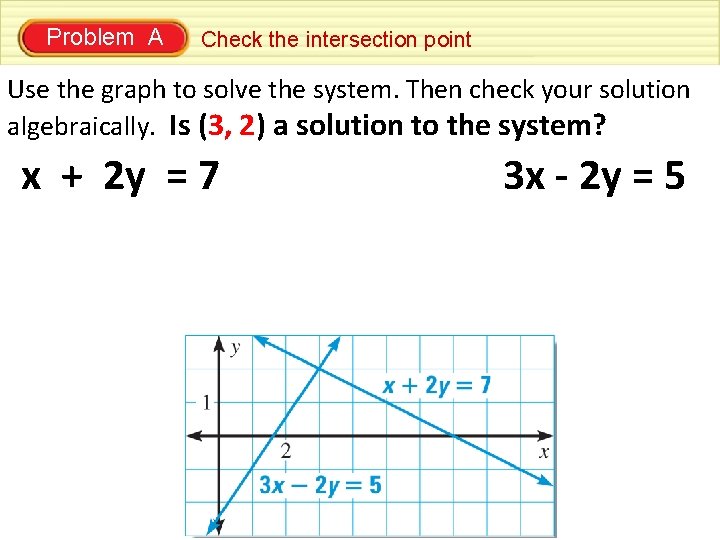
Problem A Check the intersection point Use the graph to solve the system. Then check your solution algebraically. Is (3, 2) a solution to the system? x + 2 y = 7 3 x - 2 y = 5

Problem A Check the intersection point SOLUTION Use the graph to solve the system. Then check your solution algebraically. Is (3, 2) a solution to the system? x + 2 y = 7 (3) + 2(2) = 7 3+4=7 7=7 YES, it is a solution of the linear system because the ordered pair (3, 2) is a solution of each equation. 3 x - 2 y = 5 3(3) -2(2) = 5 9– 4=5 5=5

Problem B Check the intersection point Check your solution algebraically. Is (1, 2) a solution to the system? -x + 2 y = 3 2 x + y = 4

Problem B Check the intersection point SOLUTION Check your solution algebraically. Is (1, 2) a solution to the system? -x + 2 y = 3 -(1) + 2(2) = 3 -1 + 4 = 3 3=3 YES, it is a solution of the linear system because the ordered pair (1, 2) is a solution of each equation. y= 2 -x + 3 2 x + y = 4 2(1) + (2) = 4 2+2=4 4=4 solution 2 x (1, 2) +y =4 y = (1/2) x + (3/2) y = -2 x + 4

Storm Check (Think, Write, Discuss, Report) What do you have to do to check that a given ordered pair is a solution for the system of equations? To check if a given ordered pair is a solution for the system of equations, I have to ____________________________.

Problem A Use the Graph and Check Method Step 1: Graph Both Equations in the same plane Step 2: Find coordinates of the point of intersection Step 3: Check each equation to verify solution Solve the System of Equations: Eq. 1: -x + y = -7 STEP 1 Graph both equations Eq. 2: x + 4 y = -8 STEP 2 Find intersection. STEP 3 Check solution Eq. 1: -x + y = -7 Eq. 2: x + 4 y = -8

Problem A Use the Graph and Check Method SOLUTION Step 1: Graph Both Equations in the same plane Step 2: Find coordinates of the point of intersection Step 3: Check each equation to verify solution Solve the System of Equations: Eq. 1: -x + y = -7 y = x -7 STEP 1 Graph both equations y = mx + b STEP 2 Find intersection. (4, -3) Eq. 2: x + 4 y = -8 4 y = -x -8 y = -(1/4)x -2 y = mx + b STEP 3 Check solution Eq. 1: -x + y = -7 -(4) + (-3) = -7 -4 – 3 = -7 -7 = -7 Eq. 2: x + 4 y = -8 4 + 4(-3) = -8 4 – 12 = -8 -8 = -8

Problem B Use the Graph and Check Method Step 1: Graph Both Equations in the same plane Step 2: Find coordinates of the point of intersection Step 3: Check each equation to verify solution Solve the System of Equations: Eq. 1: -5 x + y = 0 STEP 1 Graph both equations Eq. 2: 5 x + y = 10 STEP 2 Find intersection. STEP 3 Check solution Eq. 1: -5 x + y = 0
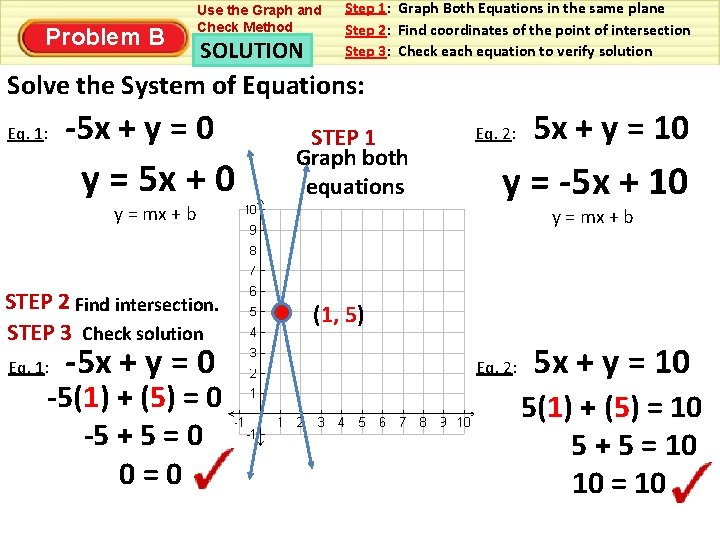
Problem B Use the Graph and Check Method SOLUTION Step 1: Graph Both Equations in the same plane Step 2: Find coordinates of the point of intersection Step 3: Check each equation to verify solution Solve the System of Equations: Eq. 1: -5 x + y = 0 y = 5 x + 0 STEP 1 Graph both equations y = mx + b STEP 2 Find intersection. STEP 3 Check solution Eq. 1: -5 x + y = 0 -5(1) + (5) = 0 -5 + 5 = 0 0=0 Eq. 2: 5 x + y = 10 y = -5 x + 10 y = mx + b (1, 5) Eq. 2: 5 x + y = 10 5(1) + (5) = 10 5 + 5 = 10 10 = 10

Storm Check (Think, Write, Discuss, Report) When you look at a graph of a system of linear equations, where do you see the solution? When I look at a graph of a system of linear equations, I can see the solution _____________________________.

Problem A Solve a multi-step problem A business rents in-line skates and bicycles. During one day, the business has a total of 25 rentals and collects $ 450 for the rentals. Find the number of pairs of skates rented and the number of bicycles rented. STEP 1 Write a linear system. STEP 2 Graph both equations. STEP 3 Estimate point of intersection. STEP 4 Check solution RENTAL BUSINESS

Problem A Solve a multi-step problem A business rents in-line skates and bicycles. During one day, the business has a total of 25 rentals and collects $ 450 for the rentals. Find the number of pairs of skates rented and the number of bicycles rented. STEP 1 Write a linear system. STEP 2 Graph both equations. STEP 3 Estimate point of intersection. STEP 4 Check solution RENTAL BUSINESS

Problem A RENTAL BUSINESS Solve a multi-step problem SOLUTION A business rents in-line skates and bicycles. During one day, the business has a total of 25 rentals and collects $ 450 for the rentals. Find the number of pairs of skates rented and the number of bicycles rented. STEP 1 Write a linear system. Let x be the number of pairs of skates rented, and let y be the number of bicycles rented. Rentals x + y = 25 15 x + 30 y = 450 Money Collected STEP 2 Graph both equations. STEP 3 Estimate the point of intersection. STEP 4 Check solution x + y = 25 (20) + (5) = 25 25 = 25 (20, 5) 15 x + 30 y = 450 15(20) + 30(5) = 450 300 + 150 = 450

Problem B Solve a multi-step problem WHAT IF? A business rents in-line skates and bicycles. During one day, the business has a total of 18 rentals and collects $ 390 for the rentals. Find the number of pairs of skates rented and the number of bicycles rented. STEP 1 Write a linear system. STEP 2 Graph both equations. STEP 3 Estimate point of intersection. STEP 4 Check solution RENTAL BUSINESS

Problem B Solve a multi-step problem WHAT IF? A business rents in-line skates and bicycles. During one day, the business has a total of 18 rentals and collects $ 390 for the rentals. Find the number of pairs of skates rented and the number of bicycles rented. STEP 1 Write a linear system. STEP 2 Graph both equations. STEP 3 Estimate point of intersection. STEP 4 Check solution RENTAL BUSINESS

Problem B RENTAL BUSINESS Solve a multi-step problem WHAT IF? SOLUTION A business rents in-line skates and bicycles. During one day, the business has a total of 18 rentals and collects $ 390 for the rentals. Find the number of pairs of skates rented and the number of bicycles rented. STEP 1 Write a linear system. Let x be the number of pairs of skates rented, and let y be the number of bicycles rented. Rentals x + y = 18 15 x + 30 y = 390 Money Collected STEP 2 Graph both equations. STEP 3 Estimate the point of intersection. y = -x + 18 STEP 4 Check solution (10, 8) y = -(1/2)x + 13 x + y = 18 (10) + (8) = 18 18 = 18 15 x + 30 y = 390 15(10) + 30(8) = 390 150 + 240 = 390

Vocabulary 1) System of Linear Equations 2) Solution to a System of Equations 3) Solve by Graphing 4) Solve by Elimination 5) Solve by Substitution

Home Work 1 -2 -3: 2) Section 7. 1 Pg. 378 -381 Txt. Bk. Prob. #3, 5, 15, 23, 31, 35 Solved and Put in Binder? Date 1) Class 4 -Square Notes Put In Binder? 3) Section ______ Notes Copied on blank sheet of paper in Binder? Table of Contents Description Date Due

Title: 7. 1 Solve Linear Systems by Graphing Date: Learning Target By the end of the period, I will solve linear systems by graphing I will demonstrate this by completing Four. Square Notes and by solving problems in a pair/group activity.
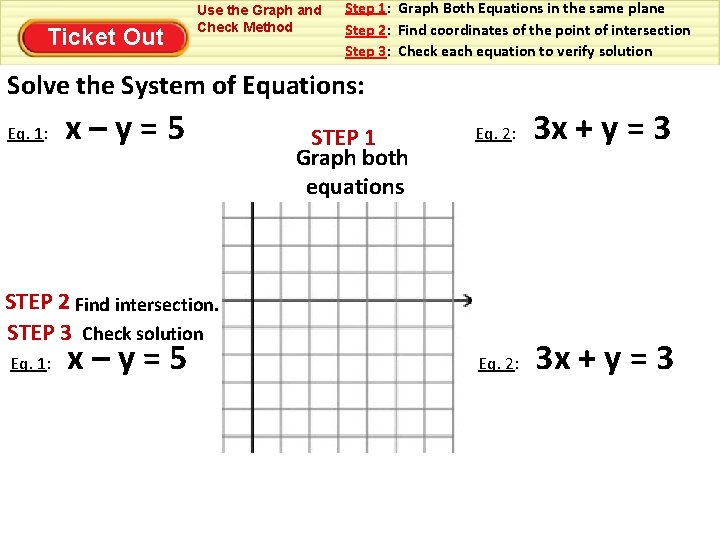
Ticket Out Use the Graph and Check Method Step 1: Graph Both Equations in the same plane Step 2: Find coordinates of the point of intersection Step 3: Check each equation to verify solution Solve the System of Equations: Eq. 1: x–y=5 STEP 1 Graph both equations Eq. 2: 3 x + y = 3 STEP 2 Find intersection. STEP 3 Check solution Eq. 1: x–y=5
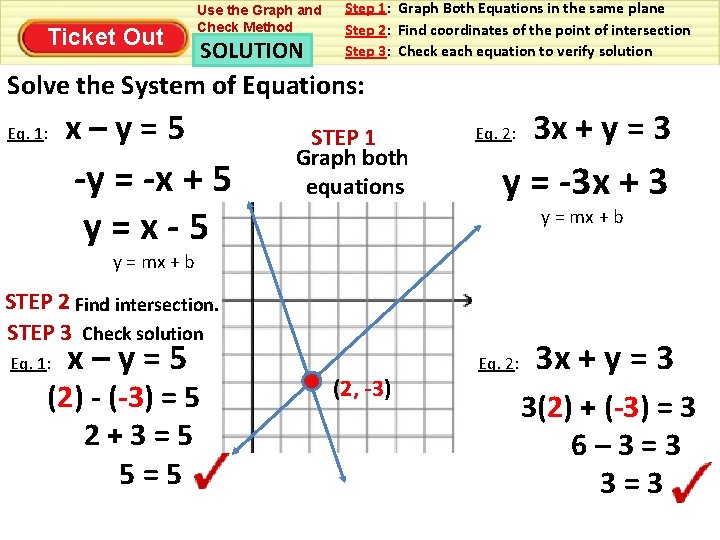
Ticket Out Use the Graph and Check Method SOLUTION Step 1: Graph Both Equations in the same plane Step 2: Find coordinates of the point of intersection Step 3: Check each equation to verify solution Solve the System of Equations: Eq. 1: x–y=5 -y = -x + 5 y=x-5 STEP 1 Graph both equations Eq. 2: 3 x + y = 3 y = -3 x + 3 y = mx + b STEP 2 Find intersection. STEP 3 Check solution Eq. 1: x–y=5 (2) - (-3) = 5 2+3=5 5=5 (2, -3) Eq. 2: 3 x + y = 3 3(2) + (-3) = 3 6– 3=3
- Slides: 30