Mrsekkdols optimalizlsa a szagls nhny sztochasztikus reakcikinetikai modelljben

Mérések/kódolás optimalizálása a szaglás néhány sztochasztikus reakciókinetikai modelljében a Fisherféle információ alapján Tóth János (lektorált cikk nyomán) 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 1

Vázlat • Lektorálás • Sztochasztikus reakciókinetika • A szaglás egy részletének néhány egyszerű modellje • Kritériumok becslések jóságára 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 2

A radioaktív bomlásnak avagy a baktériumok szaporodásának determinisztikus modellje • • • x(t+h)=x(t)-k x(t) h+ε(h) h ]t, t+h[ x’(t)=-k x(t) x(0)=M x(t)=Cexp(-kt) C=M Baktériumoknál k<0 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. lim+0 ε=0 3

A modell jellemzői • Pozitív • Szigorúan monton • Nullához/végtelenhez tart • Folytonos idejű • Folytonos állapotterű: (CCD) 2020. 10. 28. • Diszkrét részecskék • Nem szig mon • Folytonos idejű, • diszkrét állapotterű, • sztochasztikus (CDS) kívánatosabb lenne. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 4

A radioaktív bomlás sztochasztikus modellje • • Pn(t): =P(X(t)=n) n→n-1 knh+ε(h)h Pn(t+h)= k(n+1)h. Pn+1(t)+(1 -knh) Pn(t)+ε(h)h Pn’(t)=k(n+1)Pn+1(t)-knh. Pn(t) Pn(0)=δn. M Nagy (1023) lin. dersz Sztoch. , diszkrét, átlagban konzisztens 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 5

Kémiai reakciók • A+B↔C • (a, b, c)→(a-1, b-1, c+1) • Közelítő konzisztencia: Rényi, 1953 k 1 abh+ ε(h)h • (a, b, c)→(a+1, b+1, c-1) • E(α)’=-k 1 E(αβ)+k 2 E(γ) k 2 c+ε(h)h • Pn’(t)=… 2020. 10. 28. • Általános tételek: Kurtz, 1972 Formális reakciókinetikai szeminárium, BME Anal. Tszk. 6

RÉNYI Alfréd (1921 -1970) 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 7

Még két fontos személy • Max DELBRÜCK, 1906 -1981 2020. 10. 28. • Thomas KURTZ Formális reakciókinetikai szeminárium, BME Anal. Tszk. 8

Populációbiológia • X→ 2 X X+Y→ 2 Y Y→ 0 • Volterra-Lotka modell • Kvalitatív különbségek: mindkét faj kihal 2020. 10. 28. • Alfred James LOTKA 1880 -1949 Formális reakciókinetikai szeminárium, BME Anal. Tszk. 9

Közgazdaságtan • n→n+1 αnh+ ε(h)h • n→n-1 βnh+ε(h)h • (az ár a kereslet és a kínálat miatt föl és le) • Születési-halálozási folyamat • Átlagban konzisztens • Stabilizálódik az ár 2020. 10. 28. • Walras, Marie-Esprit. Leon (1834 -1910) Formális reakciókinetikai szeminárium, BME Anal. Tszk. 10

Problémák, megoldások • Általános egyenletek • Létezés, egyértelműség stb. • Exponenciális várakozási idő két ugrás között→szimuláció 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 11

Előnyök, hátrányok • Részletesebb betekintés • Fizikailag reálisabb • (CDS) 2020. 10. 28. • Matematikailag bonyolultabb • Sok gépidő kell (computationally intensive ) • Jobb adatok kellenek Formális reakciókinetikai szeminárium, BME Anal. Tszk. 12

Szaglásmodellezők: P. Lánsky, J. -P. Rospars 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 13

Részlet: biokémia • • • Kaszkád, ioncsatorna, akciós potenciál s C(s) (aktivált komplex), ill. s kódolás Konc. det. : közvetlen, gyors, rev. transzfer Fluxusdet. : lassú, irrev, degradáció 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 14

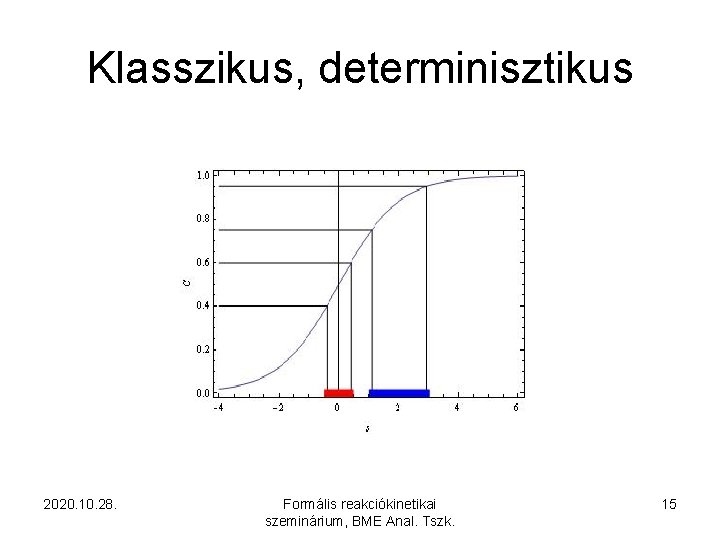
Klasszikus, determinisztikus 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 15

Koncentrációdetektor • Egyféle szaganyag (ligandum), mennyisége kint: L=exp(s) állandó! • Egy kötőhely minden receptoron • Rögz. receptorszám: N 2020. 10. 28. • • (L+)R↔C Szül. -hal. foly λi: =k 1(N-i)exp(s) μi: =k-1 i C stac. eloszlása: B(N, 1/(1+Kexp(-s))) Vhó érték, variancia Formális reakciókinetikai szeminárium, BME Anal. Tszk. 16

Ornstein-Uhlenbeck-közelítéssel • Ct~λN/(1+N)+Ut√N = N/(1+Kexp(-s))+Ut√N • d. Ut = -(k 1 exp(s)+k-1)Utdt +[√(2 k 1 k-1 exp(s))/(k 1 exp(s)+k-1)]d. Wt ennek alapján normális közelítés, CCS modell • Tuckwell, Kurtz • vagy: közvetlenül a közp. hatelo. tétel 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 17

Elfoglalt→aktivált (2 modell) • p valószínűséggel aktiválódik • B(N, p/(1+Kexp(-s))) 2020. 10. 28. • • két lépésben: R↔C* C*↔C Állapottér: vektor Formális reakciókinetikai szeminárium, BME Anal. Tszk. 18

Fluxusdetektor • Ex→L • L+R↔C→R+Degr. L • Most L nem állandó 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 19

Milyen pontosan becsülhető a szaganyag koncja a válasz alapján? (Becslés ill. kódolás) • C(s)-ből s meghat. • Klasszikus, determinisztikus mo. : ismert az s f(s) bemenet-kimenet fv. , vagy: jelválasz fv. Ott mérünk, ahol a deriváltja maximális. • J 1(s): =∂E(C(s))/∂s • s-et C(s)-re vonatkozó mintából akarjuk becsülni, krit. : a Fisher-információ legyen maximális (vö. Andai A. Ph. Dje) 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 20

FISHER, Sir Ronald Aylmer 18901962 • was an English statistician, evolutionary biologist, and geneticist. He was described by Anders Hald as "a genius who almost singlehandedly created the foundations for modern statistical science" and Richard Dawkins described him as "the greatest of Darwin's successors". 2020. 10. 28. Formális reakciókinetikai szeminárium, BME Anal. Tszk. 21

J(s): =E[g’(s)/g(s)] • Ui. a Cramér-Rao szerint: • Var(s^)≥ 1/J(s) • amikor szimbolikusan nem számolható, akkor van alsó becslés: J(s) ≥ • J 2(s): =J 1(s)2/Var(C(s)) • néha = áll. 2020. 10. 28. • Az egyes modellekben kiszámolják, közel vannak, de látszik, hogy az eltérés hogyan függ a paraméterektől Formális reakciókinetikai szeminárium, BME Anal. Tszk. 22