MR Review Lecture 4 MR 2 D Projection

MR Review Lecture 4 MR: 2 D Projection Reconstruction, 2 D FT Longitudinal Magnetization returns to equilibrium as Transverse Magnetization Gradients’ effect on B-field’s effect on frequency

MR Review (2) Signal Equation Signal equation related to k-space The MR signal is always telling us a point of the frequency domain expression for M, the Fourier Transform of m(x, y), the proton density of the image. The mapping between s(t) and the points in k -space is determined by the gradient waveforms.

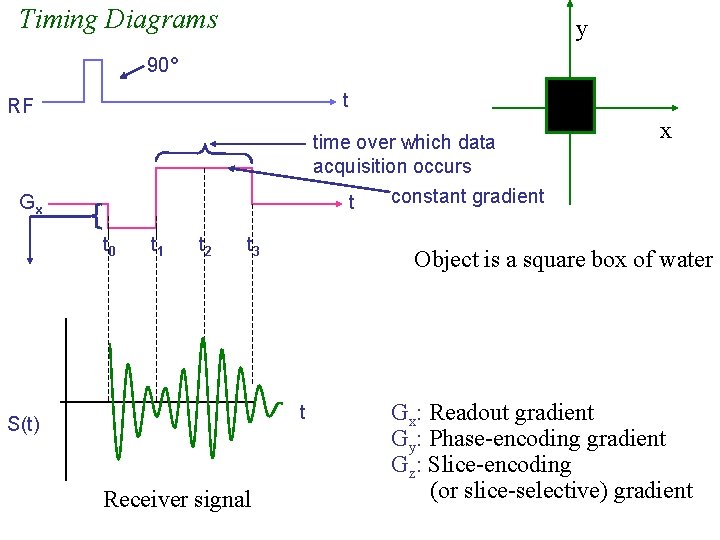
Timing Diagrams y 90° t RF time over which data acquisition occurs constant gradient t Gx t 0 t 1 t 2 t 3 Object is a square box of water t S(t) Receiver signal x Gx: Readout gradient Gy: Phase-encoding gradient Gz: Slice-encoding (or slice-selective) gradient

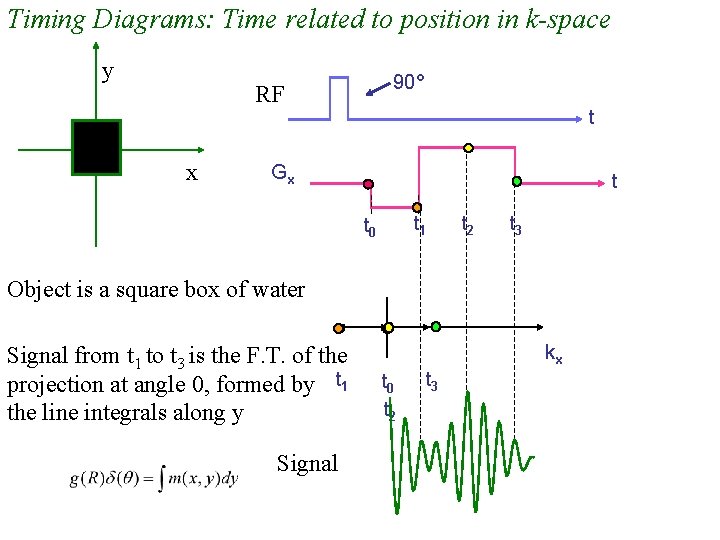
Timing Diagrams: Time related to position in k-space y 90° RF x t Gx t t 1 t 0 t 2 t 3 Object is a square box of water Signal from t 1 to t 3 is the F. T. of the projection at angle 0, formed by t 1 the line integrals along y Signal kx t 0 t 2 t 3

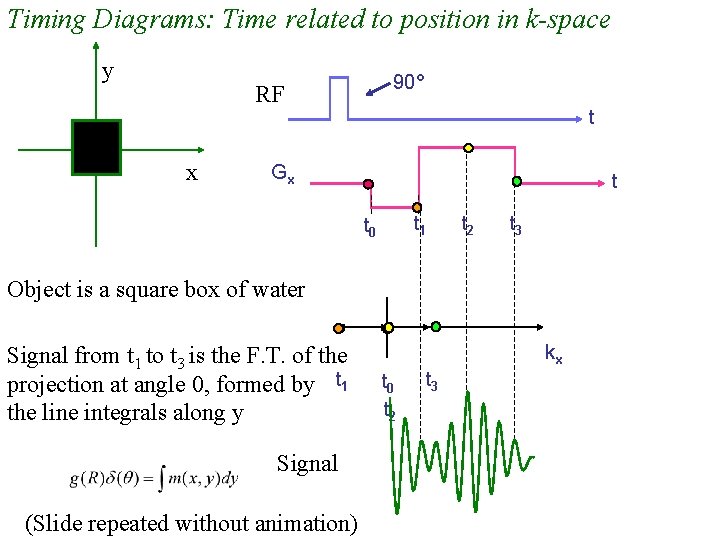
Timing Diagrams: Time related to position in k-space y 90° RF x t Gx t t 1 t 0 t 2 t 3 Object is a square box of water Signal from t 1 to t 3 is the F. T. of the projection at angle 0, formed by t 1 the line integrals along y Signal (Slide repeated without animation) kx t 0 t 2 t 3

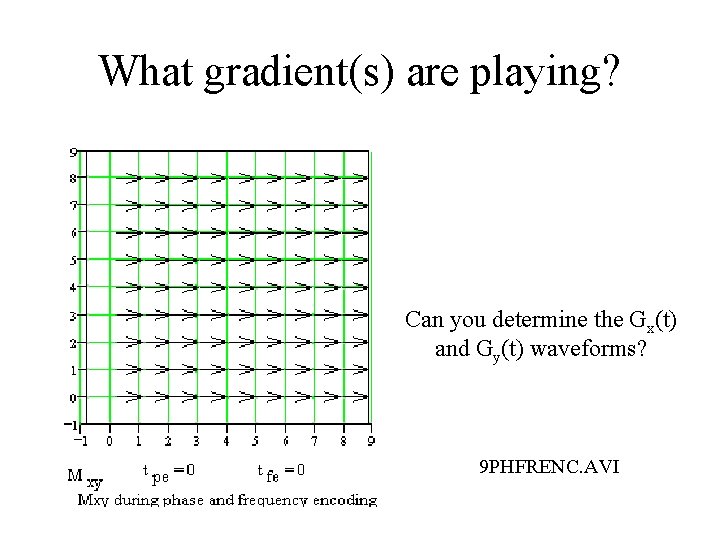
What gradient(s) are playing? Can you determine the Gx(t) and Gy(t) waveforms? 9 PHFRENC. AVI

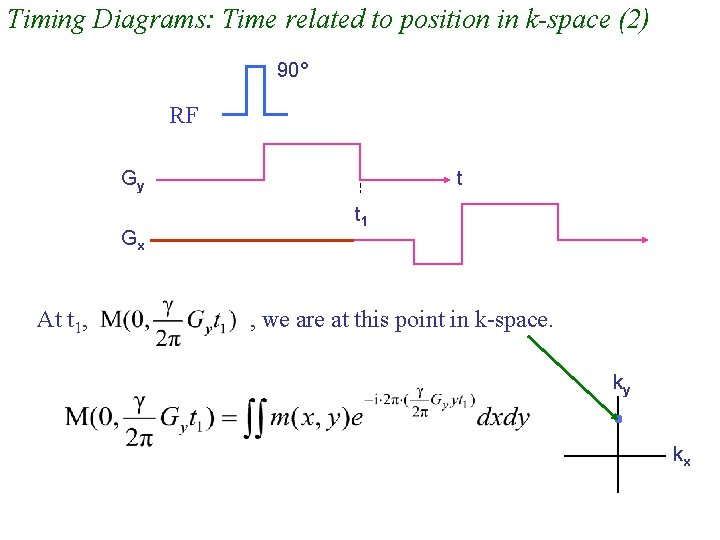
Timing Diagrams: Time related to position in k-space (2) 90° RF Gy Gx At t 1, t t 1 , we are at this point in k-space. ky kx

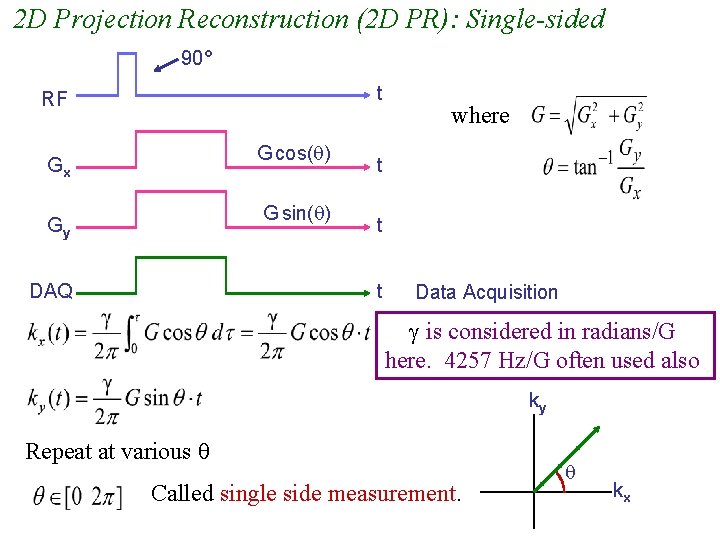
2 D Projection Reconstruction (2 D PR): Single-sided 90° t RF G cos( ) Gx G sin( ) Gy DAQ where t t t Data Acquisition is considered in radians/G here. 4257 Hz/G often used also ky Repeat at various Called single side measurement. kx

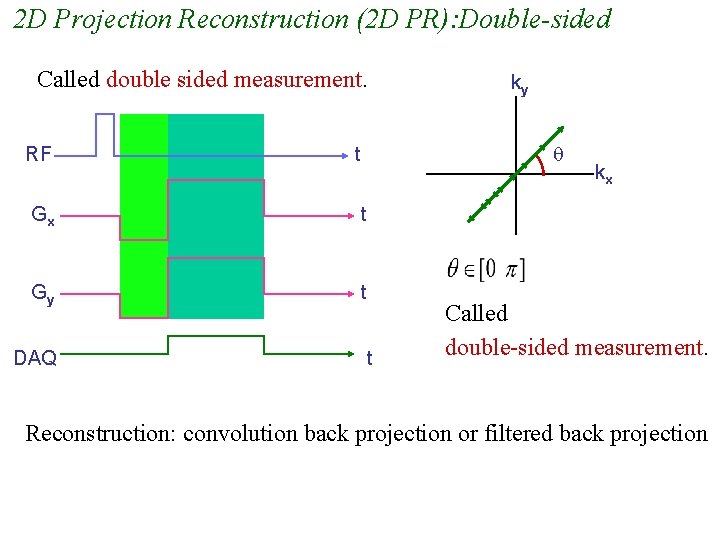
2 D Projection Reconstruction (2 D PR): Double-sided Called double sided measurement. RF t Gx t Gy t DAQ ky t kx Called double-sided measurement. Reconstruction: convolution back projection or filtered back projection

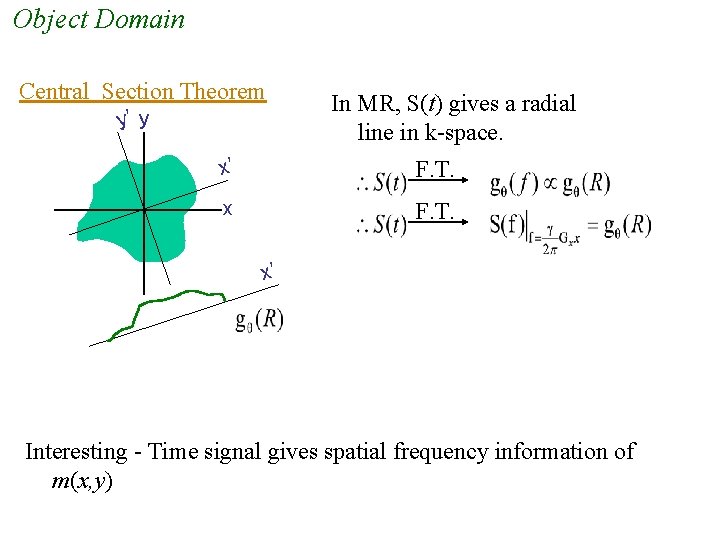
Object Domain Central Section Theorem y’ y In MR, S(t) gives a radial line in k-space. x’ F. T. x F. T. x’ Interesting - Time signal gives spatial frequency information of m(x, y)

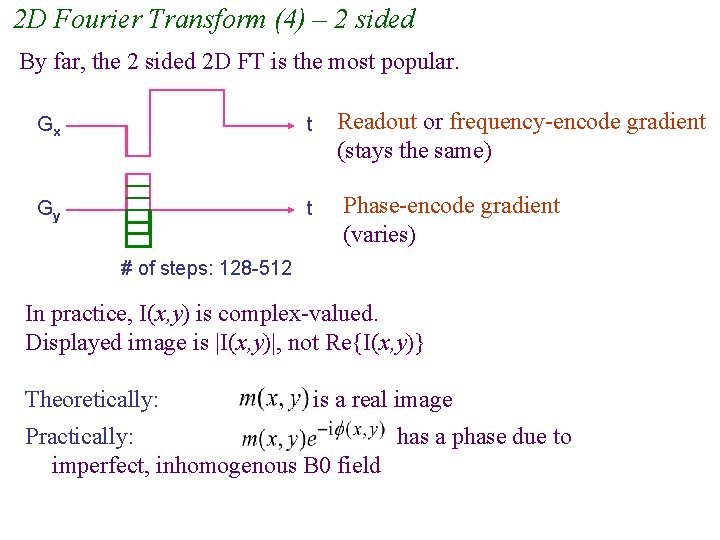
2 D Fourier Transform (4) – 2 sided By far, the 2 sided 2 D FT is the most popular. Gx t Readout or frequency-encode gradient (stays the same) Gy t Phase-encode gradient (varies) # of steps: 128 -512 In practice, I(x, y) is complex-valued. Displayed image is |I(x, y)|, not Re{I(x, y)} Theoretically: is a real image Practically: has a phase due to imperfect, inhomogenous B 0 field

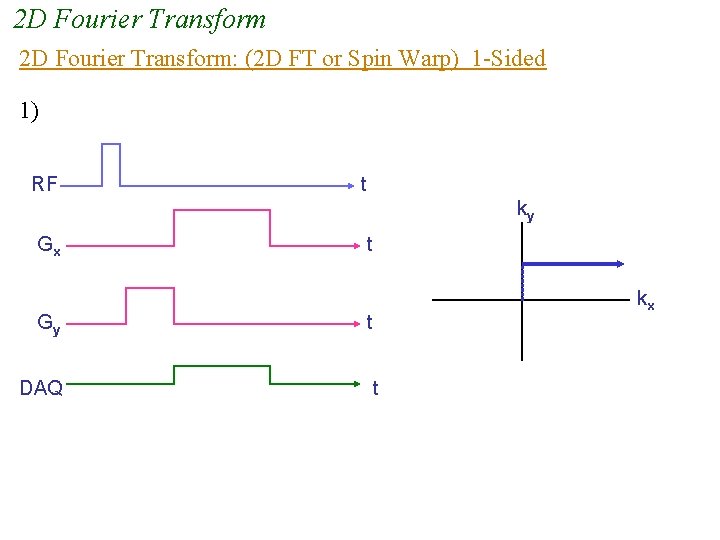
2 D Fourier Transform: (2 D FT or Spin Warp) 1 -Sided 1) RF t ky Gx Gy DAQ t kx t t

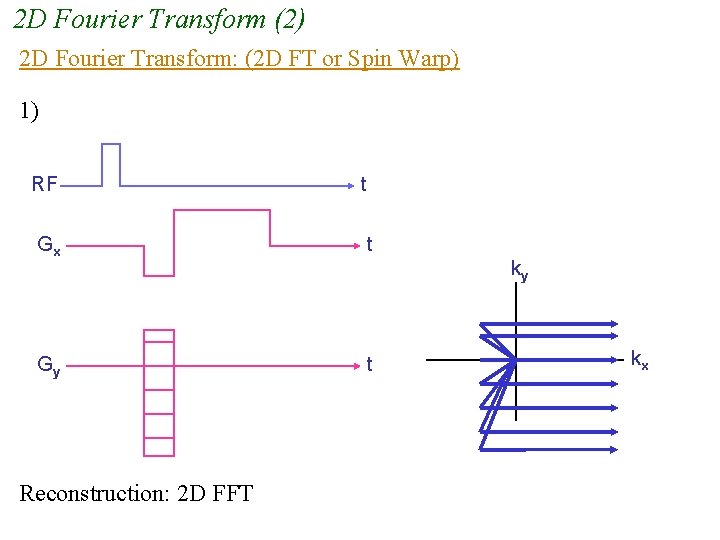
2 D Fourier Transform (2) 2 D Fourier Transform: (2 D FT or Spin Warp) 1) RF t Gx t Gy t Reconstruction: 2 D FFT ky kx

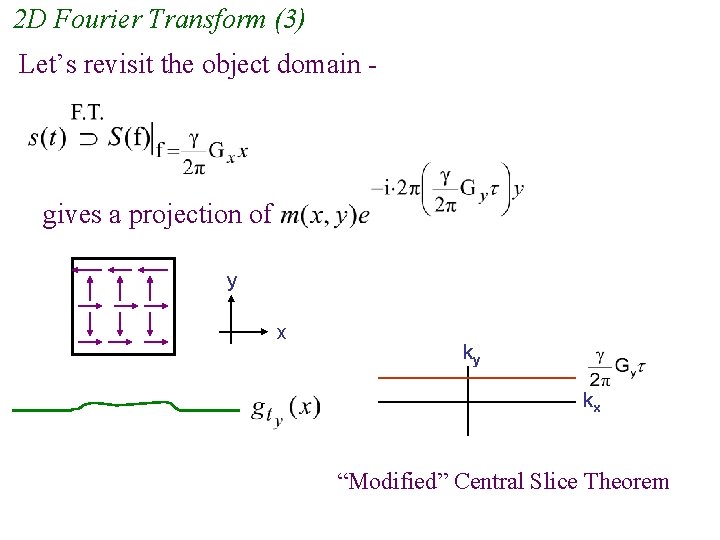
2 D Fourier Transform (3) Let’s revisit the object domain - gives a projection of y x ky kx “Modified” Central Slice Theorem

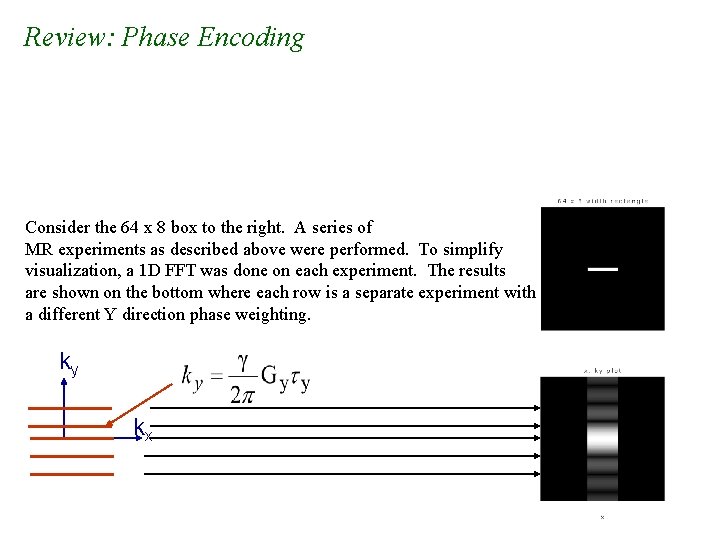
Review: Phase Encoding Consider the 64 x 8 box to the right. A series of MR experiments as described above were performed. To simplify visualization, a 1 D FFT was done on each experiment. The results are shown on the bottom where each row is a separate experiment with a different Y direction phase weighting. ky kx

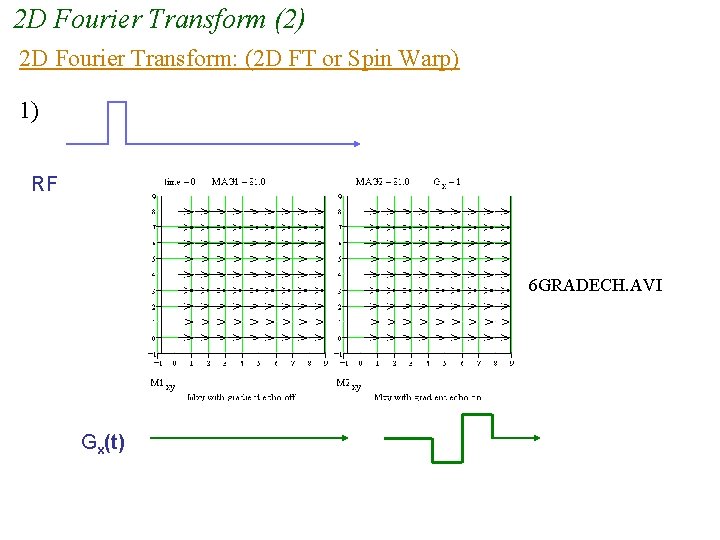
2 D Fourier Transform (2) 2 D Fourier Transform: (2 D FT or Spin Warp) 1) RF t 6 GRADECH. AVI Gx(t)