MPI Tutorial Examples Based on Michael Quinns Textbook

MPI Tutorial • Examples Based on Michael Quinn’s Textbook • Example 1: Circuit Satisfiability Check (Chapter 4) • Example 2: Sieve of Eratosthenes (Chapter 5) • Example 3: Floyd’s Algorithm (Chapter 6) • Example 4: Matrix-Vector Multiplication (Chapter 8) • Example 5: Document Classification (Chapter 9) Sahalu Junaidu ICS 573: High Performance Computing 1

Example 1: Circuit Satisfiability • This problem requires determining whether a given circuit is satisfiable. – Find the set of input combinations (if any) for which the circuit output 1 • This problem is important for the design and verification of logical devices. • This problem is NP-complete and one way to solve it is to try every combination of circuit inputs • For a circuit with k inputs, there are 2 k combinations since every input can take two values, 0 and 1. • MPI functions introduced in this example – – – – MPI_Init – to initialize MPI_Comm_rank – to determine a process’s ID number MPI_Comm_size – to find the number of processes MPI_Reduce – to perform a reduction operation MPI_Finalize – to shut down MPI_Barrier – to perform barrier synchronization MPI_Wtime – to determine the time MPI_Wtick – to find the accuracy of the timer Sahalu Junaidu ICS 573: High Performance Computing 2

Example: Circuit Satisfiability Sahalu Junaidu ICS 573: High Performance Computing 3

Example: Circuit Satisfiability (cont’d) • We may decompose this problem by associating one task with each combination of input. – A task displays its input combination that satisfies the circuit • Characteristics of the tasks – Fixed in number (for a given circuit) – No communication between tasks (tasks independent of each other) – Time needed per task is variable • Use cyclic distribution in an effort to balance the computational load. – With n pieces of work, 0, 1, 2, …, n-1 and p processes, assign work unit k to process k mod p. • Parallel code version 1 is here. Sahalu Junaidu ICS 573: High Performance Computing 4

Example: Circuit Satisfiability (cont’d) • Compiling: mpicc -o <exec> <source 1> <source 2> … • Specifying host processors • Running: mpirun -np <p> <exec> <arg 1> … – -np <p> number of processes – <exec> executable – <arg 1> … command-line arguments Sahalu Junaidu ICS 573: High Performance Computing 5

Example: Enhancing the Program • We want to find total number of solutions • Incorporate sum-reduction into program • Modify function check_circuit – Return 1 if circuit satisfiable with input combination – Return 0 otherwise • Each process keeps local count of satisfiable circuits it has found • Perform reduction after for loop • This version of the program is here. Sahalu Junaidu ICS 573: High Performance Computing 6

Example: Benchmarking the Program • MPI_Barrier barrier synchronization • MPI_Wtime current time – Returns an elapsed (wall clock) time on the calling processor • MPI_Wtick – returns, as a double precision value, the number of seconds between successive clock ticks. – For example, if the clock is implemented by the hardware as a counter that is incremented every millisecond, the value returned by MPI_WTICK should be 10 -3 • Benchmarking code: double elapsed_time; … MPI_Init (&argc, &argv); MPI_Barrier (MPI_COMM_WORLD); elapsed_time = - MPI_Wtime(); … MPI_Reduce (…); elapsed_time += MPI_Wtime(); Sahalu Junaidu ICS 573: High Performance Computing 7

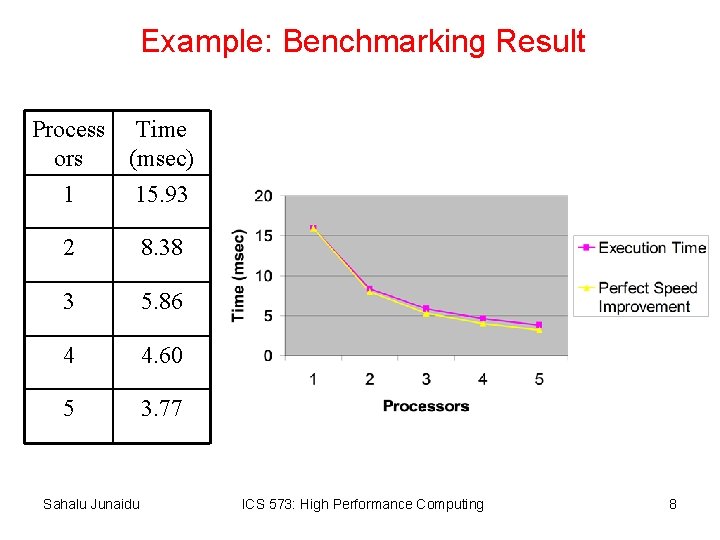
Example: Benchmarking Result Process Time ors (msec) 1 15. 93 2 8. 38 3 5. 86 4 4. 60 5 3. 77 Sahalu Junaidu ICS 573: High Performance Computing 8

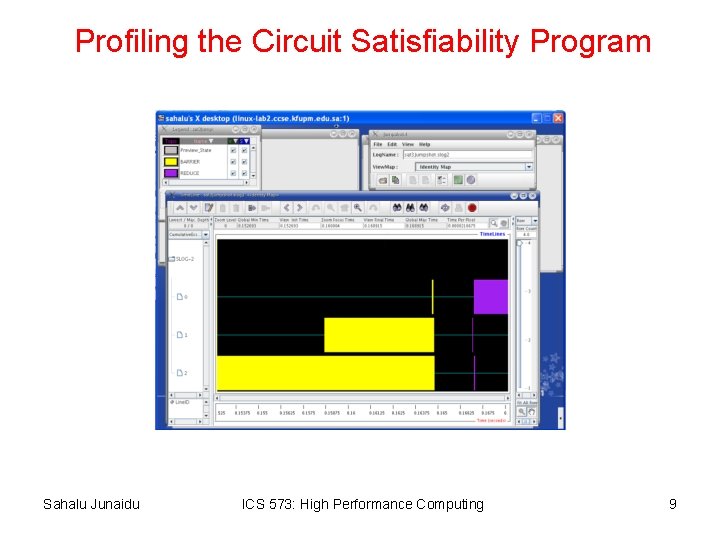
Profiling the Circuit Satisfiability Program Sahalu Junaidu ICS 573: High Performance Computing 9

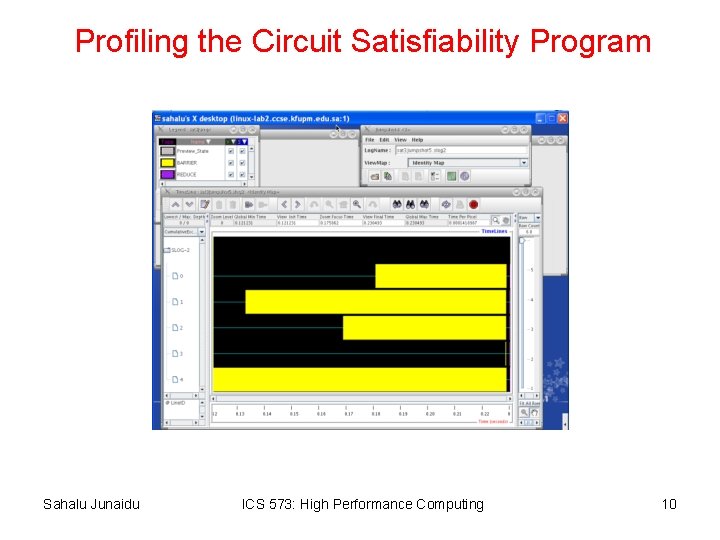
Profiling the Circuit Satisfiability Program Sahalu Junaidu ICS 573: High Performance Computing 10

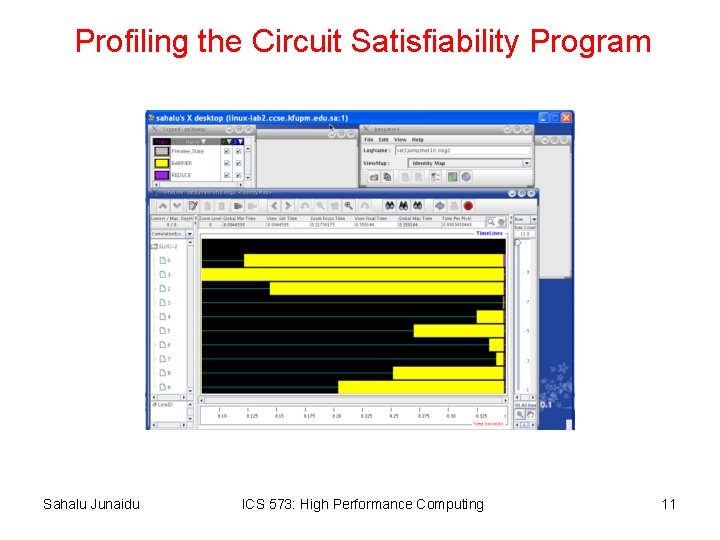
Profiling the Circuit Satisfiability Program Sahalu Junaidu ICS 573: High Performance Computing 11

Discussion • Assume n pieces of work, p processes, and cyclic allocation – What is the most pieces of work any process has? – What is the least pieces of work any process has? – How many processes have the most pieces of work? Sahalu Junaidu ICS 573: High Performance Computing 12

Example 2: Sieve of Eratosthenes • Sieve of Eratosthenes is a classical way of extracting prime numbers from a series of all integers starting from 2 • First number, 2, is prime and kept. • All multiples of this number are deleted as they cannot be prime. • Process repeated with each remaining number. • The algorithm removes nonprimes, leaving only primes. • MPI function introduced in this example – MPI_Bcast – to broadcast a message to all processes in a communicator Sahalu Junaidu ICS 573: High Performance Computing 13

Sieve of Eratosthenes: Sequential Algorithm 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 Sahalu Junaidu ICS 573: High Performance Computing 14

Sieve of Eratosthenes: Sequential Algorithm for(i=2; i<=n; i++) prime[i] = 0; /* initialize array */ for(i=2; i<=sqrt_n; i++) /* for each prime */ if (prime[i]==0) for(j=i*i; j<=n; j = j+i) prime[j] = 1; /* strike its multiples */ Sahalu Junaidu ICS 573: High Performance Computing 15

Sieve of Eratosthenes: Sequential Algorithm 1. Create list of unmarked natural numbers 2, 3, …, n 2. k 2 3. Repeat (a) Mark all multiples of k between k 2 and n (b) k smallest unmarked number > k until k 2 > n 4. The unmarked numbers are primes Sahalu Junaidu ICS 573: High Performance Computing 16

Making 3(a) Parallel Mark all multiples of k between k 2 and n for all j where k 2 j n do if j mod k = 0 then mark j (it is not a prime) endif endfor Sahalu Junaidu ICS 573: High Performance Computing 17

Making 3(b) Parallel • Find smallest unmarked number > k • Min-reduction (to find smallest unmarked number > k) • Broadcast (to get result to all tasks) Sahalu Junaidu ICS 573: High Performance Computing 18

Sieve of Eratosthenes: Parallelization Options • Make each process handle one array element – Lots of data parallelism – Lots of communication (a reduce and a broadcast in each iteration) • Make each process strike out one number – Leads to load imbalance – Repeated work when done naively • Pipelining • Cyclic allocation – Leads to load imbalance for this problem – Easy to determine “owner” of each index • Block allocation – Balances loads – More complicated to determine owner if n not a multiple of p Sahalu Junaidu ICS 573: High Performance Computing 19

Advantages of Block Decomposition: No Reduction • Largest prime used to sieve is n • First process has n/p elements • It has all sieving primes if p < n • First process always broadcasts next sieving prime • No reduction step needed Sahalu Junaidu ICS 573: High Performance Computing 20

Advantages of Block Decomposition: Fast Marking • Block decomposition allows same marking as sequential algorithm: j, j + k, j + 2 k, j + 3 k, … instead of for all j in block if j mod k = 0 then mark j (it is not a prime) Sahalu Junaidu ICS 573: High Performance Computing 21

Block Decomposition Macros #define BLOCK_LOW(id, p, n) ((i)*(n)/(p)) #define BLOCK_HIGH(id, p, n) (BLOCK_LOW((id)+1, p, n)-1) #define BLOCK_SIZE(id, p, n) (BLOCK_HIGH(id, p, n)-BLOCK_LOW(id, p, n)+1) #define BLOCK_OWNER(index, p, n) (((p)*(index)+1)-1)/(n)) Sahalu Junaidu ICS 573: High Performance Computing 22

Function MPI_Bcast int MPI_Bcast ( void *buffer, /* Addr of 1 st element */ /* # elements to broadcast */ int count, MPI_Datatype datatype, /* Type of elements */ /* ID of root process */ int root, MPI_Comm comm) /* Communicator */ MPI_Bcast (&k, 1, MPI_INT, 0, MPI_COMM_WORLD); • Complete code is here. Sahalu Junaidu ICS 573: High Performance Computing 23

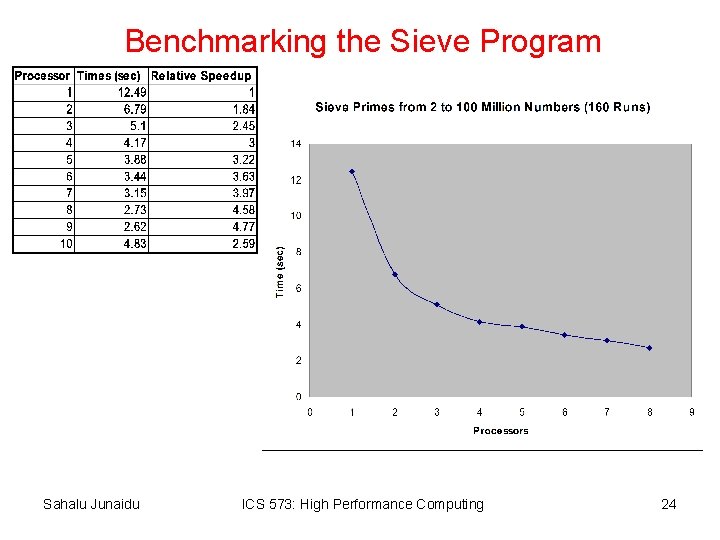
Benchmarking the Sieve Program Sahalu Junaidu ICS 573: High Performance Computing 24

Profiling the Sieve Program Sahalu Junaidu ICS 573: High Performance Computing 25

Profiling the Sieve Program Sahalu Junaidu ICS 573: High Performance Computing 26

Profiling the Sieve Program Sahalu Junaidu ICS 573: High Performance Computing 27

Improving the Sieve Program • The performance of the Sieve program can be improved by – Deleting even integers – Eliminating broadcast • If only odd integers are represented – storage requirements of the program can be halved and – the speed of marking multiples of a particular prime can be doubled • Eliminate broadcast by replicating the odd integers 3, 5, 7, …, n on each process – Each process can then use the sequential algorithm to find the primes in this range – After that each process can sieve its n/p portion of the larger array without a broadcast Sahalu Junaidu ICS 573: High Performance Computing 28

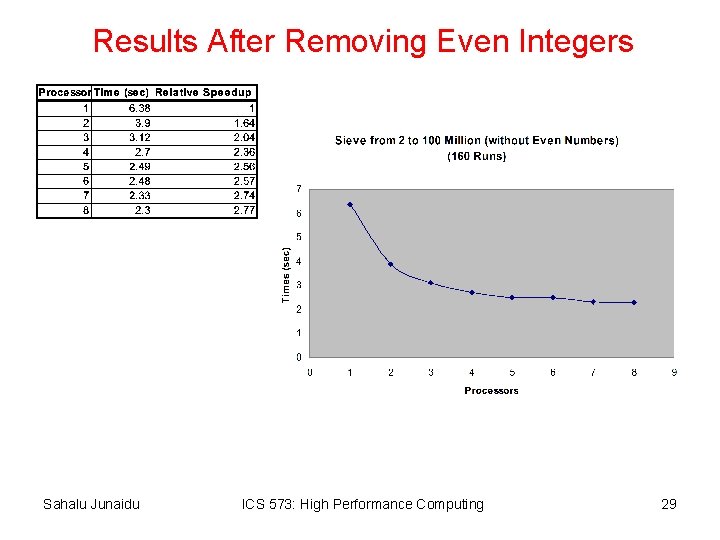
Results After Removing Even Integers Sahalu Junaidu ICS 573: High Performance Computing 29

Jumpshot Visualization After Removing Even Integers Sahalu Junaidu ICS 573: High Performance Computing 30

Jumpshot Visualization After Removing Even Integers Sahalu Junaidu ICS 573: High Performance Computing 31

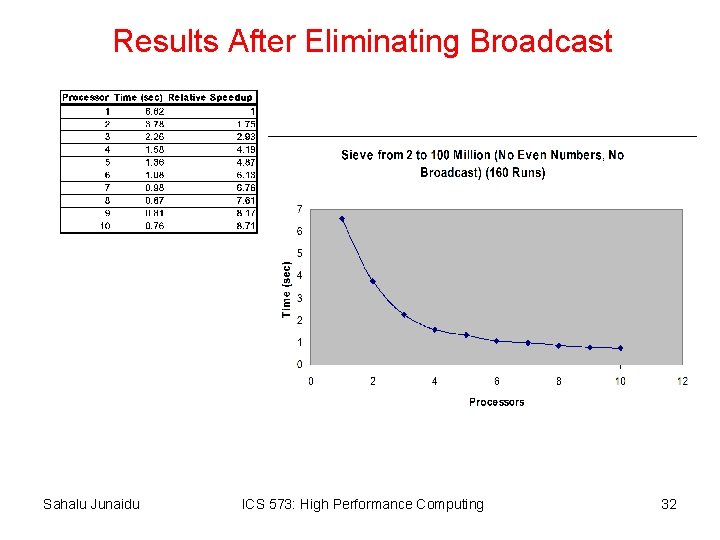
Results After Eliminating Broadcast Sahalu Junaidu ICS 573: High Performance Computing 32

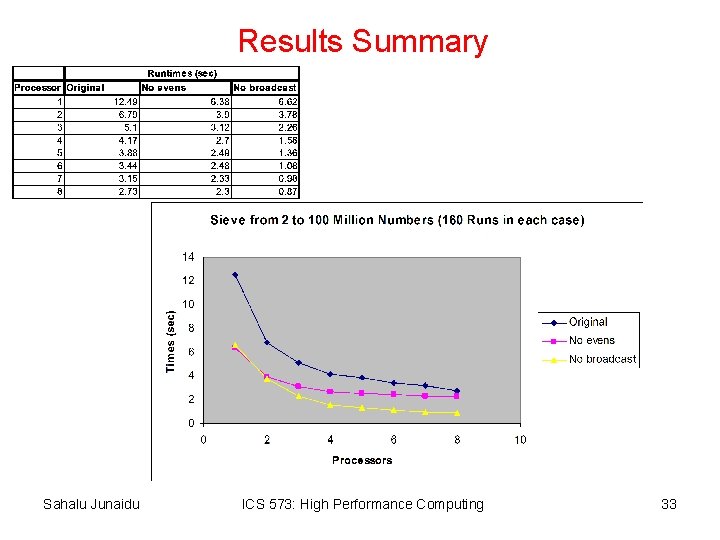
Results Summary Sahalu Junaidu ICS 573: High Performance Computing 33

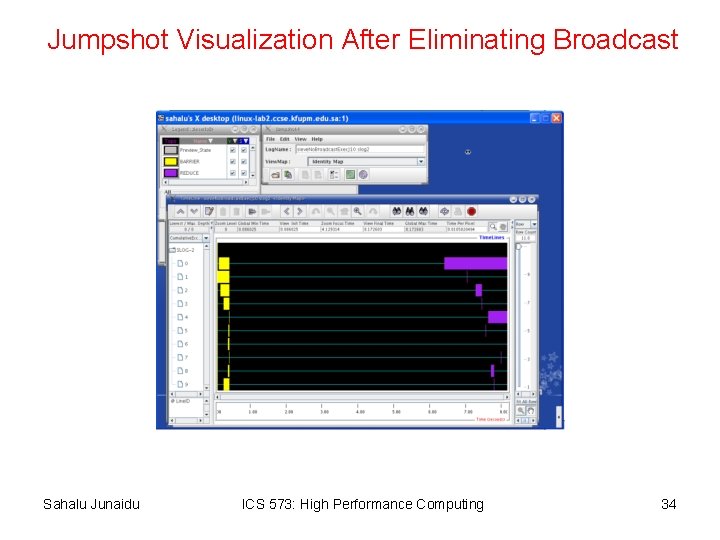
Jumpshot Visualization After Eliminating Broadcast Sahalu Junaidu ICS 573: High Performance Computing 34

Example 3: Floyd’s Algorithm • Floyd’s algorithm is a classic algorithm used to solve the all-pairs shortest-path problem. • It uses the dynamic programming (DP) method to solve the problem on a dense graph. • DP is used to solve a wide variety of discrete optimization problems such as scheduling, etc. • DP breaks problems into subproblems and combine their solutions into solutions to larger problems. • In contrast to divide-and-conquer, there may be interrelationships across subproblems. • MPI functions introduced in this example – MPI_Send – which allows a process to send a message to another process – MPI_Recv – which allows a process to receive a message from another process Sahalu Junaidu ICS 573: High Performance Computing 35

Sequential Floyd’s Algorithm for k 0 to n-1 for i 0 to n-1 for j 0 to n-1 a[i, j] min (a[i, j], a[i, k] + a[k, j]) endfor Sahalu Junaidu ICS 573: High Performance Computing 36

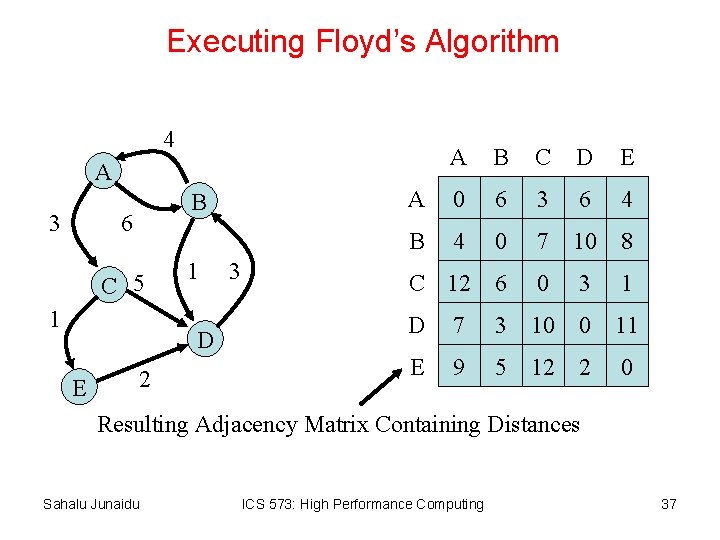
Executing Floyd’s Algorithm 4 A B C D E A 0 6 3 6 4 B 4 0 7 10 8 C 12 6 0 3 1 D 7 3 10 0 11 E 9 5 12 2 0 A 3 B 6 C 5 1 1 D E 2 3 Resulting Adjacency Matrix Containing Distances Sahalu Junaidu ICS 573: High Performance Computing 37

Tracing Floyd’s Algorithm (iteration k=0) i=0, j=0, 1, 2, 3, 4 A[0, 0]=MIN(A[0, 0], A[0, 0]+A[0, 0])=0 A[0, 1]=MIN(A[0, 1], A[0, 0]+A[0, 1])=6 A[0, 2]=MIN(A[0, 2], A[0, 0]+A[0, 2])=3 A[0, 3]=MIN(A[0, 3], A[0, 0]+A[0, 3])=INF A[0, 4]=MIN(A[0, 4], A[0, 0]+A[0, 4])=INF i=3, j=0, 1, 2, 3, 4 A[3, 0]=MIN(A[3, 0], A[3, 0]+A[0, 0])=INF A[3, 1]=MIN(A[3, 1], A[3, 0]+A[0, 1])=3 A[3, 2]=MIN(A[3, 2], A[3, 0]+A[0, 2])=INF A[3, 3]=MIN(A[3, 3], A[3, 0]+A[0, 3])=0 A[3, 4]=MIN(A[3, 4], A[3, 0]+A[0, 4])=INF i=1, j=0, 1, 2, 3, 4 A[1, 0]=MIN(A[1, 0], A[1, 0]+A[0, 0])=4 A[1, 1]=MIN(A[1, 1], A[1, 0]+A[0, 1])=0 A[1, 2]=MIN(A[1, 2], A[1, 0]+A[0, 2])=7 A[1, 3]=MIN(A[1, 3], A[1, 0]+A[0, 3])=1 A[1, 4]=MIN(A[1, 4], A[1, 0]+A[0, 4])=INF i=4, j=0, 1, 2, 3, 4 A[4, 0]=MIN(A[4, 0], A[4, 0]+A[0, 0])=INF A[4, 1]=MIN(A[4, 1], A[4, 0]+A[0, 1])=INF A[4, 2]=MIN(A[4, 2], A[4, 0]+A[0, 2])=INF A[4, 3]=MIN(A[4, 3], A[4, 0]+A[0, 3])=2 A[4, 4]=MIN(A[4, 4], A[4, 0]+A[0, 4])=0 i=2, j=0, 1, 2, 3, 4 A[2, 0]=MIN(A[2, 0], A[2, 0]+A[0, 0])=INF A[2, 1]=MIN(A[2, 1], A[2, 0]+A[0, 1])=INF A[2, 2]=MIN(A[2, 2], A[2, 0]+A[0, 2])=0 A[2, 3]=MIN(A[2, 3], A[2, 0]+A[0, 3])=5 A[2, 4]=MIN(A[2, 4], A[2, 0]+A[0, 4])=1 Sahalu Junaidu ICS 573: High Performance Computing 38

Tracing Floyd’s Algorithm (iteration k = 1) i=0, j=0, 1, 2, 3, 4 A[0, 0]=MIN(A[0, 0], A[0, 1]+A[1, 0])=0 A[0, 1]=MIN(A[0, 1], A[0, 1]+A[1, 1])=6 A[0, 2]=MIN(A[0, 2], A[0, 1]+A[1, 2])=3 A[0, 3]=MIN(A[0, 3], A[0, 1]+A[1, 3])=7 A[0, 4]=MIN(A[0, 4], A[0, 1]+A[1, 4])=INF i=3, j=0, 1, 2, 3, 4 A[3, 0]=MIN(A[3, 0], A[3, 1]+A[1, 0])=7 A[3, 1]=MIN(A[3, 1], A[3, 1]+A[1, 1])=3 A[3, 2]=MIN(A[3, 2], A[3, 1]+A[1, 2])=10 A[3, 3]=MIN(A[3, 3], A[3, 1]+A[1, 3])=0 A[3, 4]=MIN(A[3, 4], A[3, 1]+A[1, 4])=INF i=1, j=0, 1, 2, 3, 4 A[1, 0]=MIN(A[1, 0], A[1, 1]+A[1, 0])=4 A[1, 1]=MIN(A[1, 1], A[1, 1]+A[1, 1])=0 A[1, 2]=MIN(A[1, 2], A[1, 1]+A[1, 2])=7 A[1, 3]=MIN(A[1, 3], A[1, 1]+A[1, 3])=1 A[1, 4]=MIN(A[1, 4], A[1, 1]+A[1, 4])=INF i=4, j=0, 1, 2, 3, 4 A[4, 0]=MIN(A[4, 0], A[4, 1]+A[1, 0])=INF A[4, 1]=MIN(A[4, 1], A[4, 1]+A[1, 1])=INF A[4, 2]=MIN(A[4, 2], A[4, 1]+A[1, 2])=INF A[4, 3]=MIN(A[4, 3], A[4, 1]+A[1, 3])=2 A[4, 4]=MIN(A[4, 4], A[4, 1]+A[1, 4])=0 i=2, j=0, 1, 2, 3, 4 A[2, 0]=MIN(A[2, 0], A[2, 1]+A[1, 0])=INF A[2, 1]=MIN(A[2, 1], A[2, 1]+A[1, 1])=INF A[2, 2]=MIN(A[2, 2], A[2, 1]+A[1, 2])=0 A[2, 3]=MIN(A[2, 3], A[2, 1]+A[1, 3])=5 A[2, 4]=MIN(A[2, 4], A[2, 1]+A[1, 4])=1 Sahalu Junaidu ICS 573: High Performance Computing 39

Designing Parallel Algorithm • From the pseudocode, we see that the same assignment statement is executed n 3 times – Decompose the problem by dividing matrix A into its n 2 elements • Communication – Each update of element a[i, j] requires access to elements a[i, k] and a[k, j] – Note that for any particular k, element a[k, m] is needed by every task associated with elements in column m. • Thus, during iteration k each element in row k of gets broadcast to the tasks in the same column – Similarly, for any particular value of k, element a[m, k] is needed by every task associated with elements in row m. • Thus, during iteration k each element in column k of a gets broadcast to the tasks in the same row Sahalu Junaidu ICS 573: High Performance Computing 40

Floyd’s Algorithm: Partitioning and Communication Updating a[3, 4] when k=1 Primitive tasks Iteration k: every task in row k broadcasts its value w/in task column Sahalu Junaidu Iteration k: every task in column k broadcasts its value w/in task row ICS 573: High Performance Computing 41

Designing Parallel Algorithm • Can the elements of the distance matrix be updated simultaneously? • That is, must a[i, k] and a[k, j] be computed before updating a[i, j] ? • The answer is no since the values a[i, k] and a[k, j] do not change during iteration k. • That is, during iteration k, updates to a[i, k] and a[k, j] take the forms: – a[i, k] min (a[i, k], a[i, k] + a[k, k]) – a[k, j] min (a[k, j], a[k, k] + a[k, j]) • Since all values are positive, neither a[i, k] nor a[k, j]can decrease. • Thus for each iteration k of the outer loop, we can perform the broadcasts and then update every element of the matrix in parallel. Sahalu Junaidu ICS 573: High Performance Computing 42

Designing Parallel Algorithm • Tasks characteristics: – – Number of tasks: static Communication pattern among tasks: structured Computation time per task: constant Strategy: • Agglomerate tasks to minimize communication, creating one task per MPI process • That is, agglomerate n 2 primitive tasks into p processes • Columnwise block striped – Broadcast within columns eliminated • Rowwise block striped – Broadcast within rows eliminated – Reading matrix from file simpler • Choose rowwise block striped decomposition Sahalu Junaidu ICS 573: High Performance Computing 43

Matrix I/O Functions void read_row_striped_matrix char *s, /* void ***subs, /* void **storage, /* MPI_Datatype dtype, /* int *m, /* int *n, /* MPI_Comm comm) /* ( IN - File name */ OUT - 2 D submatrix indices */ OUT - Submatrix stored here */ IN - Matrix element type */ OUT - Matrix rows */ OUT - Matrix cols */ IN - Communicator */ void print_row_striped_matrix void **a, /* IN MPI_Datatype dtype, /* IN int m, /* IN int n, /* IN MPI_Comm comm) /* IN • ( - 2 D array */ Matrix element type */ Matrix rows */ Matrix cols */ Communicator */ The complete parallel program is here. Sahalu Junaidu ICS 573: High Performance Computing 44

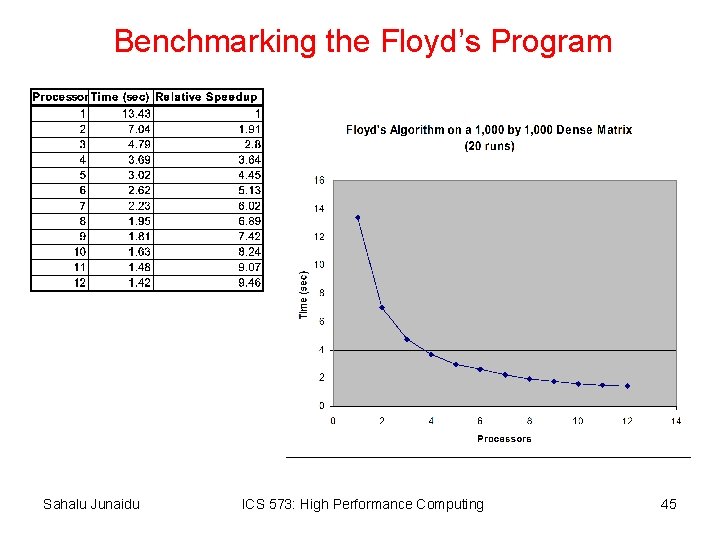
Benchmarking the Floyd’s Program Sahalu Junaidu ICS 573: High Performance Computing 45

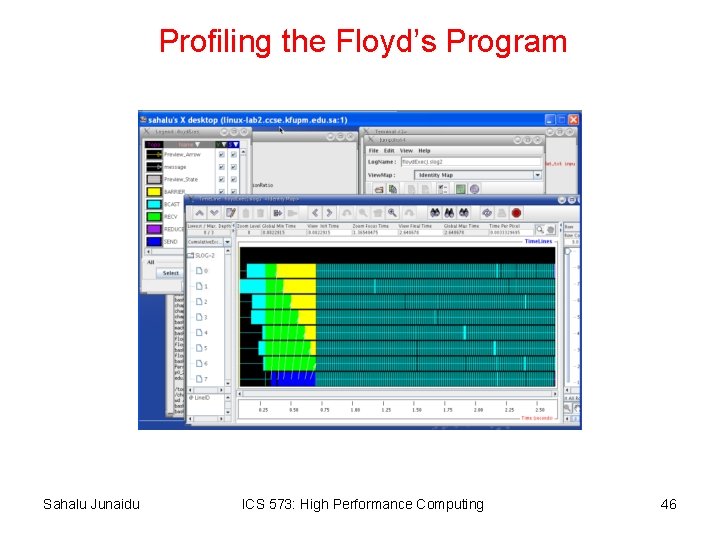
Profiling the Floyd’s Program Sahalu Junaidu ICS 573: High Performance Computing 46

Example 4: Matrix-Vector Multiplication • Matrix-vector multiplication is embedded in algorithms solving a wide variety of problems, like: – Iterative algorithms for solving systems of linear equations – Implementation of neural networks • In this example, we develop three MPI programs to multiply a dense matrix by a vector, each based on a different data decomposition • MPI functions introduced in this example – MPI_Allgatherv – an all-gather function in which different processes may contribute different numbers of elements – MPI_Scatterv – a scatter operation in which different processes may end up with different numbers of elements – MPI_Gatherv – a gather operation in which the number of elements collected from different process may vary – MPI_Alltoall – an all-to-all exchange of data elements among processes – MPI_Dims_create – provides dimensions for a balanced Cartesian grid of processes – MPI_Cart_create – creates a communicator where the processes have a Cartesian topology – MPI_Cart_coords – returns the coordinates of a specified process within a Cartesian grid – MPI_Cart_rank – returns the rank of the process at specified coordinates in a Cartesian grid – MPI_Comm_split – partitions the processes of an existing communicator into one or more groups Sahalu Junaidu ICS 573: High Performance Computing 47

Matrix-Vector Multiplication: Sequential Algorithm Input: a[0. . m-1, 0. . n-1] – an m x n matrix b[0. . n-1] – an n x 1 vector Output: c[0. . m-1] – an m x 1 vector for i 0 to m-1 c[i] 0 for j 0 to n-1 c[i]+ a[i, j] * b[j] endfor • Matrix-vector multiplication is simply a series of inner product (dot product) computations Sahalu Junaidu ICS 573: High Performance Computing 48

Data Decomposition Options • Three decomposition options for an m x n matrix: – Rowwise block-striped • Each process responsible for a contiguous group of or rows of the matrix – Columnwise block-striped • Each process responsible for a contiguous group of or columns of the matrix – Checkerboard block • Processes form a virtual grid, and the matrix is divided into 2 -D blocks aligning with that grid • Given a p-processor grid with r rows and c columns, each process is responsible for a block of the matrix containing at most rows and columns • Vectors distribution options – Replicated both vectors on each process – Block distribution option: each of the p processes is responsible for a contiguous group of either or vector elements Sahalu Junaidu ICS 573: High Performance Computing 49

Example 4. 1: Rowwise Block-Striped Decomposition • This version of the program is based on – Rowwise block-striped decompositions – Replicated vectors • First, we associate a primitive task with – each row of the matrix – replicated argument and result vectors • Tasks characteristics – – Static number of tasks Regular communication pattern (all-gather) Computation time per task is constant Strategy: Agglomerate groups of rows, creating one task per MPI process • When tasks are combined in this way, each process will compute a block of elements of the result vector. – These need to be combined to ensure that each process has all elements of the result vector Sahalu Junaidu ICS 573: High Performance Computing 50

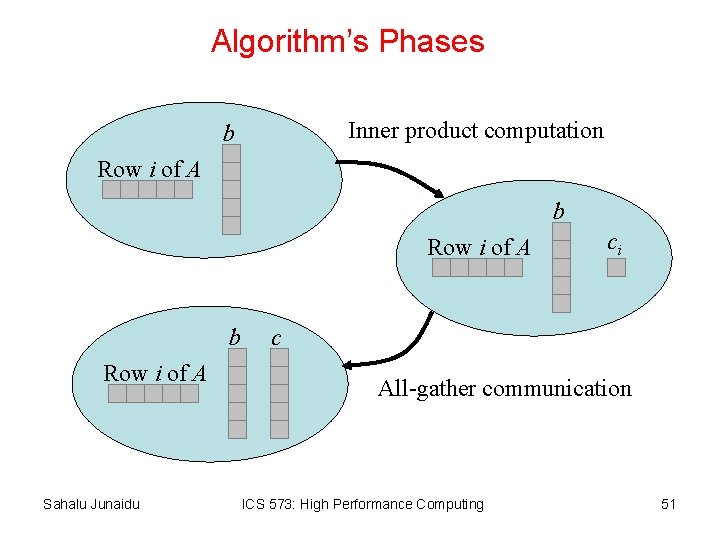
Algorithm’s Phases Inner product computation b Row i of A Sahalu Junaidu ci c All-gather communication ICS 573: High Performance Computing 51

Replicating a Block-Mapped Vector • The block of elements of the result vector computed by each process can be replicated using MPI_Allgatherv: – If the same number of items is gathered from every process, the simpler MPI_Allgather is appropriate. int MPI_Allgatherv ( void *send_buffer, int send_cnt, MPI_Datatype send_type, void *receive_buffer, int *receive_cnt, int *receive_disp, MPI_Datatype receive_type, MPI_Comm communicator) Sahalu Junaidu ICS 573: High Performance Computing 52

MPI_Allgatherv in Action Sahalu Junaidu ICS 573: High Performance Computing 53

Utility Functions: Replicating Block Vector void create_mixed_xfer_arrays ( int id, /* IN - Process rank */ int p, /* IN - Number of processes */ int n, /* IN - Total number of elements */ int **count, /* OUT - Array of counts */ int **disp) /* OUT - Array of displacements */ void replicate_block_vector ( void *ablock, /* IN - Block-distributed vector */ int n, /* IN - Elements in vector */ void *arep, /* OUT - Replicated vector */ MPI_Datatype dtype, /* IN - Element type */ MPI_Comm comm) /* IN - Communicator */ Sahalu Junaidu ICS 573: High Performance Computing 54

Utility Functions: Matrix & Vector Input void read_row_striped_matrix ( char *s, /* IN - File name */ void ***subs, /* OUT - 2 D submatrix indices */ void **storage, /* OUT - Submatrix stored here */ MPI_Datatype dtype, /* IN - Matrix element type */ int *m, /* OUT - Matrix rows */ int *n, /* OUT - Matrix cols */ MPI_Comm comm) /* IN - Communicator */ void read_replicated_vector ( char *s, /* IN - File name */ void **v, /* OUT - Vector */ MPI_Datatype dtype, /* IN - Vector type */ int *n, /* OUT - Vector length */ MPI_Comm comm) /* IN - Communicator */ • The complete parallel program is here. Sahalu Junaidu ICS 573: High Performance Computing 55

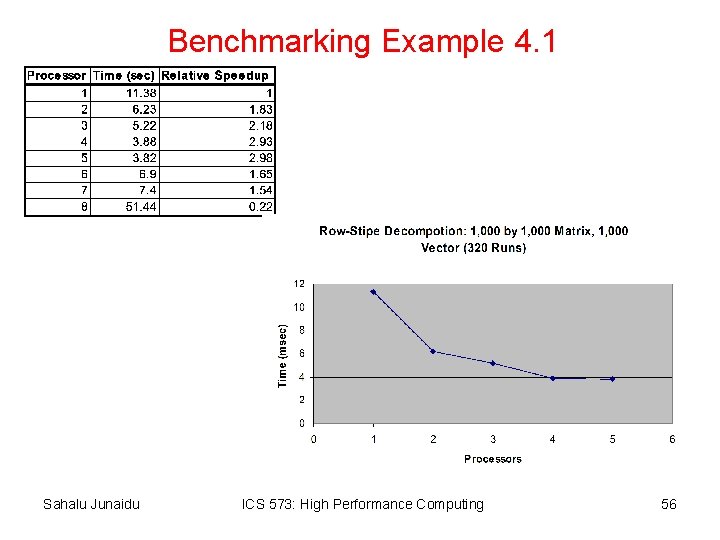
Benchmarking Example 4. 1 Sahalu Junaidu ICS 573: High Performance Computing 56

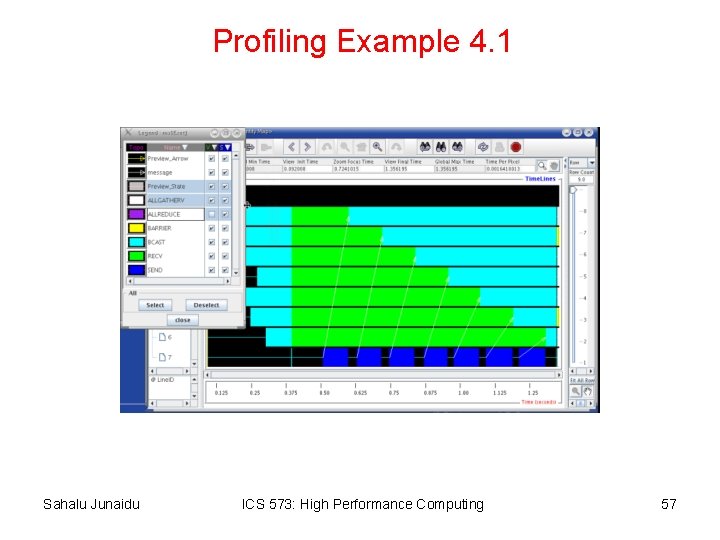
Profiling Example 4. 1 Sahalu Junaidu ICS 573: High Performance Computing 57

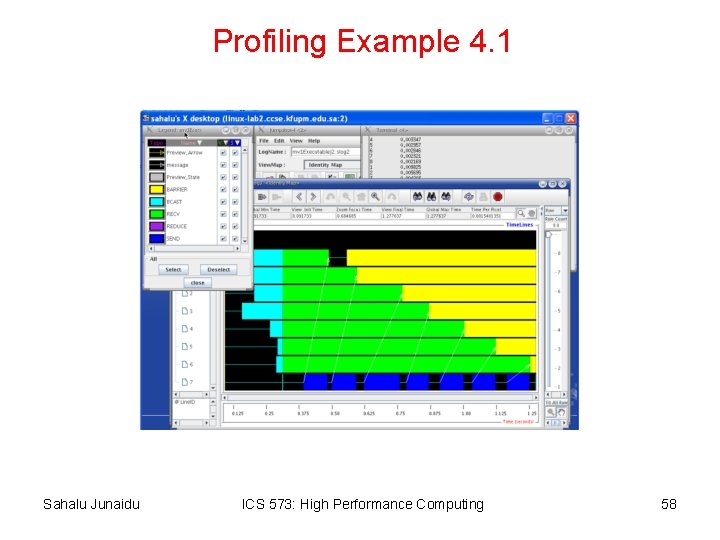
Profiling Example 4. 1 Sahalu Junaidu ICS 573: High Performance Computing 58

Example 4. 2: Columnwise Block-Striped Decomposition • This version of the program is based on – Columnwise block-striped decompositions – Block-decomposed vectors • First, we associate a primitive task i with – column i of the matrix – elements i of the argument and result vectors • Tasks characteristics – – Static number of tasks Regular communication pattern (all-to-all exchange) Computation time per task is constant Strategy: Agglomerate the primitive tasks into metatasks, mapping a metatask to an MPI process • When tasks are combined in this way, each process will compute a block of elements of the result vector. – These need to be combined to ensure that each process has all elements of the result vector Sahalu Junaidu ICS 573: High Performance Computing 59

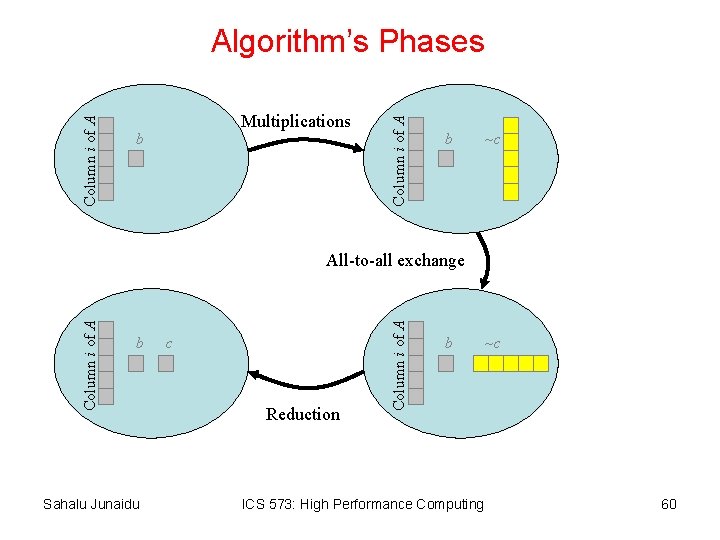
Multiplications b Column i of A Algorithm’s Phases b ~c b Sahalu Junaidu c Reduction Column i of A All-to-all exchange b ICS 573: High Performance Computing ~c 60

Exchanging Partial Inner Products • Communication required for primitive task i to produce a single element of the result vector: – All-to-all communication: every partial result element j on task i must be transferred to task j • i. e. , each task distributes n-1 terms it does not need and collect n-1 terms that it needs – At this point every task i has the n partial results it needs to add in order to produce c[i] • The same principle is extended to each metatask – Each process exchanges blocks it does not need for blocks it needs – Each metatask i receives BLOCK_SIZE(i, p, n) elements from each other task – After the exchange, i has p subarrays of size BLOCK_SIZE(i, p, n) which it needs to add to form its block of the result vector. Sahalu Junaidu ICS 573: High Performance Computing 61

Function MPI_Alltoallv int MPI_Alltoallv ( void *send_buffer, int *send_cnt, int *send_disp, MPI_Datatype send_type, void *receive_buffer, int *receive_cnt, int *receive_disp, MPI_Datatype receive_type, MPI_Comm communicator) Sahalu Junaidu ICS 573: High Performance Computing 62

Columnwise Block-Striped Matrix Input • Reading a matrix stored in row-major order and distributing it among the processes in columnwise block-striped fashion void read_col_striped_matrix char *s, void ***subs, void **storage, MPI_Datatype dtype, int *m, int *n, MPI_Comm comm) ( /* IN - File name */ /* OUT - 2 -D array */ /* OUT - Array elements */ /* IN - Element type */ /* OUT - Rows */ /* OUT - Cols */ /* IN - Communicator */ • We arrange that one process reads the matrix one row at a time and scatters it among the p processes • Thus, read_col_striped_matrix() makes use of MPI_Scatterv Sahalu Junaidu ICS 573: High Performance Computing 63

Function MPI_Scatterv int MPI_Scatterv ( void *send_buffer, int *send_cnt, int *send_disp, MPI_Datatype send_type, void *receive_buffer, int receive_cnt, MPI_Datatype receive_type, int root, MPI_Comm communicator) Sahalu Junaidu ICS 573: High Performance Computing 64

Columnwise Block-Striped Matrix Output • To ensure that values of the result matrix are printed row-wise and in correct order: – Let a single process does the printing – A gather operation is needed to print elements of each row (opposite dataflow to that of input) void print_col_striped_matrix ( void **a, /* IN - 2 D array */ MPI_Datatype dtype, /* IN - Type of matrix elements */ int m, /* IN - Matrix rows */ int n, /* IN - Matrix cols */ MPI_Comm comm) /* IN - Communicator */ • print_col_striped_matrix() makes use of MPI_Gatherv Sahalu Junaidu ICS 573: High Performance Computing 65

Function MPI_Gatherv int MPI_Gatherv void int MPI_Datatype int MPI_Comm ( *send_buffer, send_cnt, send_type, *receive_buffer, *receive_cnt, *receive_disp, receive_type, root, communicator) • Example 4. 2 parallel program is here. Sahalu Junaidu ICS 573: High Performance Computing 66

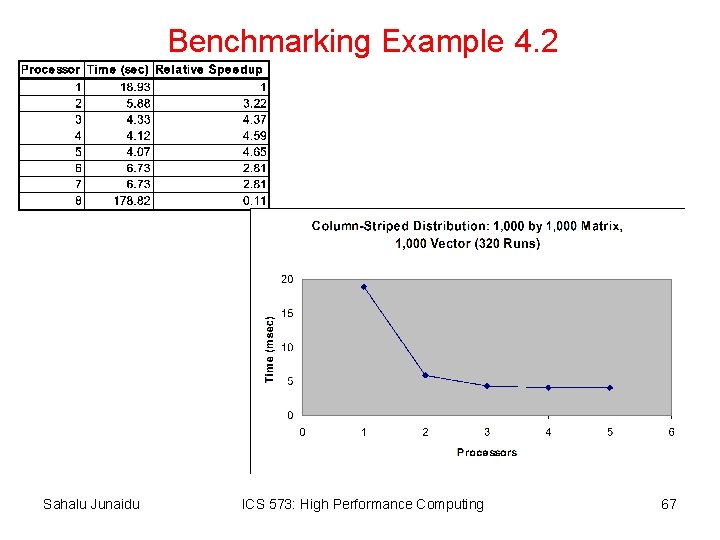
Benchmarking Example 4. 2 Sahalu Junaidu ICS 573: High Performance Computing 67

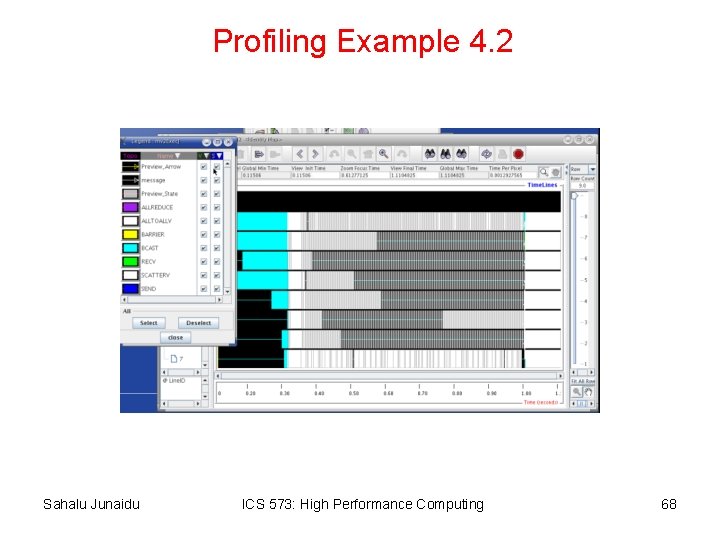
Profiling Example 4. 2 Sahalu Junaidu ICS 573: High Performance Computing 68

Example 4. 3: Checkerboard Block Decomposition • This version of the program is based on – Checkerboard (2 -D) block decomposition of the matrix – Block-decomposed vectors among processes in the first column of the process grid • First, we associate a primitive task i with – an element of the matrix • Each primitive task performs one multiply • Agglomerate primitive tasks into rectangular blocks • Processes form a 2 -D grid • The argument vector is distributed by blocks among processes in first column of grid Sahalu Junaidu ICS 573: High Performance Computing 69

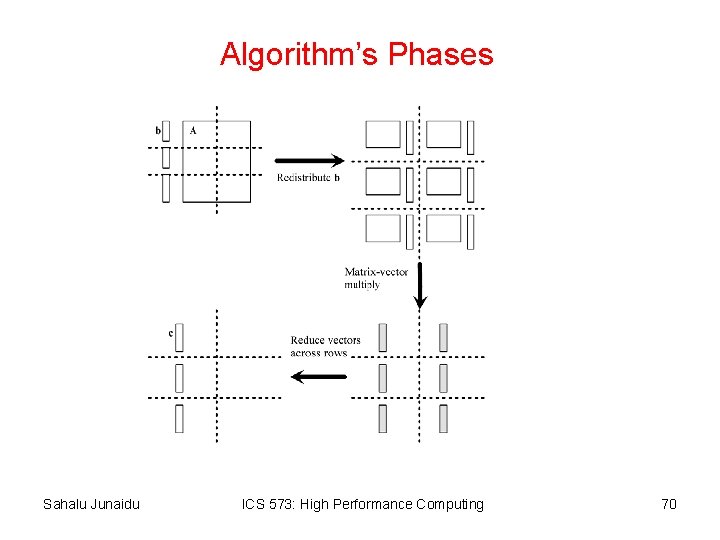
Algorithm’s Phases Sahalu Junaidu ICS 573: High Performance Computing 70

Redistributing the Argument Vector • Task associated with matrix block Ai, j performs a matrix-vector multiplication of this block with subvector bj. • Thus, we need to redistribute the vector so that each task has the correct portion of the vector • Assume the p tasks are divided into a k x l grid • Initially, divide the vector among the k tasks in the first column of the task grid • Case 1: k=l • Case 2: k /= l – After the distribution, a copy of the vector is divided among the l tasks in each row – Task at grid position (i, 0) send its portion of the vector to task at position (0, i) – Then, each process in the first row of the task grid broadcasts its portion of the vector to tasks in its column – First gather the elements of the vector onto the task at grid position (0, 0) – Next, scatter the elements of the vector among the tasks in the first row of the grid – Finally, each process in the first row of the task grid broadcasts its portion of the vector to the other tasks in the same column Sahalu Junaidu ICS 573: High Performance Computing 71

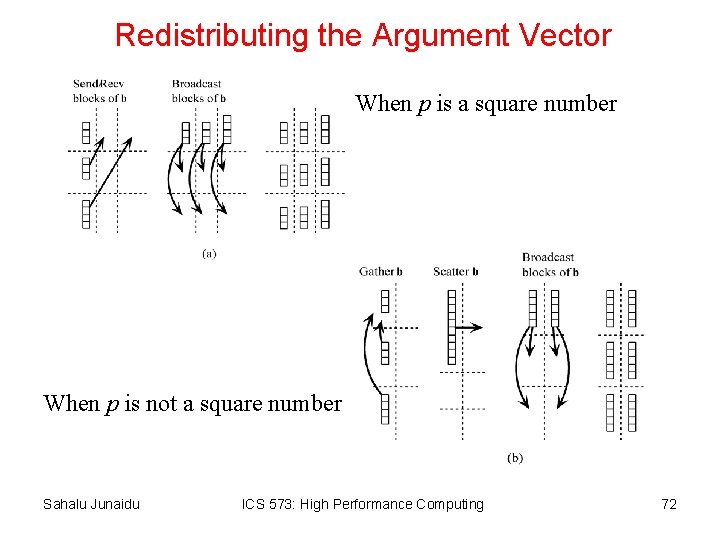
Redistributing the Argument Vector When p is a square number When p is not a square number Sahalu Junaidu ICS 573: High Performance Computing 72

Creating a Communicator • MPI_COMM_WORLD is the default communicator used when all processes are involved in collective communication. • When a subset of the processes are involved in communication, a new communicator has to be created. • Communication instances in Example 4. 3 involving subsets of processes – Gathering vector b among processes in the first column of the virtual process grid (when p is not square). – Scattering vector b among processes in the first row of the virtual process grid (when p is not square). – Broadcasting a block of b by each first-row process along its column. – Performing independent sum-reductions along each row to produce the result vector. • A communicator is a process group one of whose important attributes is topology. – A communicator’s topology enables associating an addressing scheme with the processes, other than the rank. Sahalu Junaidu ICS 573: High Performance Computing 73

Creating a Virtual Process Grid • Function MPI_Dims_creates a virtual process grid that is as close to a square as possible. int MPI_Dims_create ( int nodes, /* Input - Processes in grid */ int dims, /* Input - Number of dimensions */ int *size) /* Input/Output - Size of each grid dimension */ • The elements of size must be initialized before calling the function – If size[i]=0, the function can determine that dimension, otherwise it has been determined by the programmer. Sahalu Junaidu ICS 573: High Performance Computing 74

Creating a Virtual Process Grid • Function MPI_Cart_creates a Cartesian communicator with the desired topology. int MPI_Cart_create ( MPI_Comm old_comm, /* Input - old communicator */ int dims, /* Input - grid dimensions */ int *size, /* Input - # procs in each dim */ int *periodic, /* Input - periodic[j] is 1 if dimension j wraps around; 0 otherwise */ int reorder, /* 1 if process ranks can be reordered */ MPI_Comm *cart_comm) /* Output - new communicator */ Sahalu Junaidu ICS 573: High Performance Computing 75

Cartesian Communicator for Example 4. 3 MPI_Comm cart_comm; int periodic[2]; int size[2]; . . . size[0] = size[1] = 0; MPI_Dims_create (p, 2, size); periodic[0] = periodic[1] = 0; MPI_Cart_create (MPI_COMM_WORLD, 2, size, 1, &cart_comm); • Here is a complete example program. Sahalu Junaidu ICS 573: High Performance Computing 76

Checkberboard Matrix Input • The distribution pattern in this case is similar to that in columnwise striping – Difference: a row is scattered among a subset of the processes in this case (those in the same row of the virtual process grid) • We assume, as before, that one process is responsible for input • Each time the input process reads a row, it sends it to the first process in the appropriate row of the process grid – The first-row process then scatters the row among processes in its row of the process grid • The following grid-relation functions are needed to accomplish the matrix input: int MPI_Cart_rank () int MPI_Cart_coords () int MPI_Comm_split () Sahalu Junaidu ICS 573: High Performance Computing 77

Function MPI_Cart_rank • The rank of the process in the appropriate row of the process grid is needed in order to send a matrix row to it. • Function MPI_Cart_rank helps to determine such rank int MPI_Cart_rank ( MPI_Comm comm, /* In - Communicator */ int *coords, /* In - Array containing process’ grid location */ int *rank) /* Out - Rank of process at specified coords */ • For an r-rows process grid and m-rows input matrix, row i of the input matrix is mapped to the row of the process grid specified by BLOCK_OWNER(i, r, m). Sahalu Junaidu ICS 573: High Performance Computing 78

A Process’ Rank in A Virtual Process Grid int dest_coord[2]; /* coordinates of process receiving row */ int dest_id; /* rank of process receiving row */ int grid_id; /* rank of process in virtual grid */ int i; … for(i=0; i<m; i++){ dest_coord[0]=BLOCK_OWNER(i, r, m); dest_coord[1]=0; grid_id=MPI_Cart_rank(grid_comm, dest_coord, &dest_id); if(grid_id==0){ /* Read matrix row ‘i’ */ … /* Send matrix row ‘i’ to process ‘dest_id’ */ }else if (grid_id==dest_id){ /* Receive matrix row ‘i’ from process 0 */ … } } Sahalu Junaidu ICS 573: High Performance Computing 79

A Process’ Coordinates in A Virtual Process Grid • Function MPI_Cart_coord determines the coordinates of a process in a virtual process grid • Uses in Example 4. 3: – Allows a process to allocate the correct amount of memory for its portion of the matrix and the vector – Enables process 0 to avoid sending itself a message if it happens to be the first in a row of the process grid int MPI_Cart_coords ( MPI_Comm comm, /* In - Communicator */ int rank, /* In - Rank of process */ int dims, /* In - Dimensions in virtual grid */ int *coords) /* Out - Coordinates of specified process in virtual grid */ Sahalu Junaidu ICS 573: High Performance Computing 80

Splitting a Cartesian Communicator into Groups • The Cartesian communicator needs to be split into groups for every row in the process grid – Needed for columnwise scatter and rowwise reduce • Function MPI_Comm_split is used to achieve this int MPI_Comm_split ( MPI_Comm old_comm, /* In - Existing communicator */ int partition, /* In - Partition number */ int new_rank, /* In - Ranking order of processes in new communicator */ MPI_Comm *new_comm) /* Out - New communicator shared by processes in same partition */ • Here is an example. Sahalu Junaidu ICS 573: High Performance Computing 81

Example: Creating Communicators for Process Rows MPI_Comm grid_comm; /* 2 -D process grid */ int grid_coords[2]; /* Location of process in grid */ MPI_Comm row_comm; /* Processes in same row */ MPI_Comm_split (grid_comm, grid_coords[0], grid_coords[1], &row_comm); • Example 4. 3 parallel program is here. Sahalu Junaidu ICS 573: High Performance Computing 82

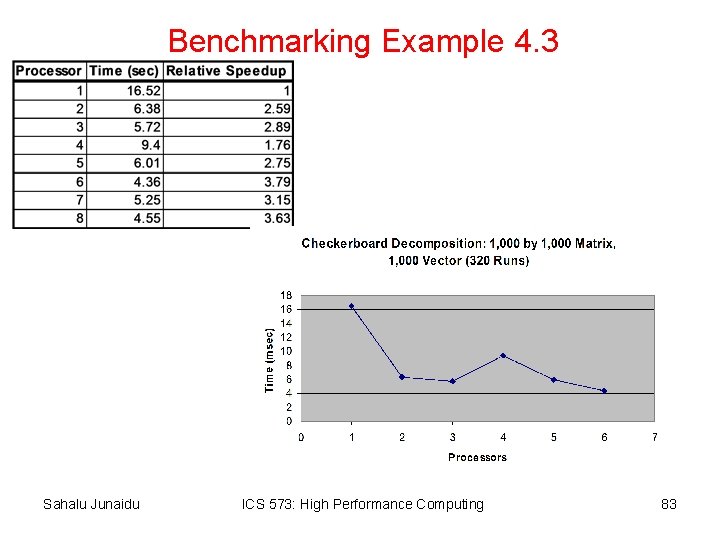
Benchmarking Example 4. 3 Sahalu Junaidu ICS 573: High Performance Computing 83

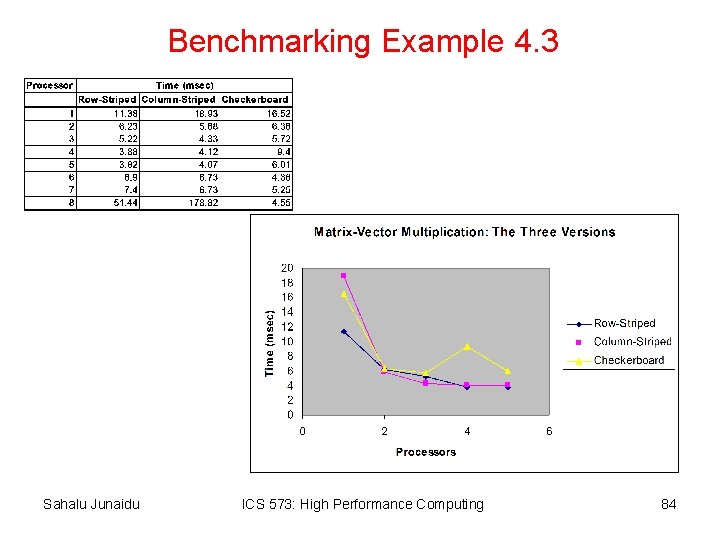
Benchmarking Example 4. 3 Sahalu Junaidu ICS 573: High Performance Computing 84

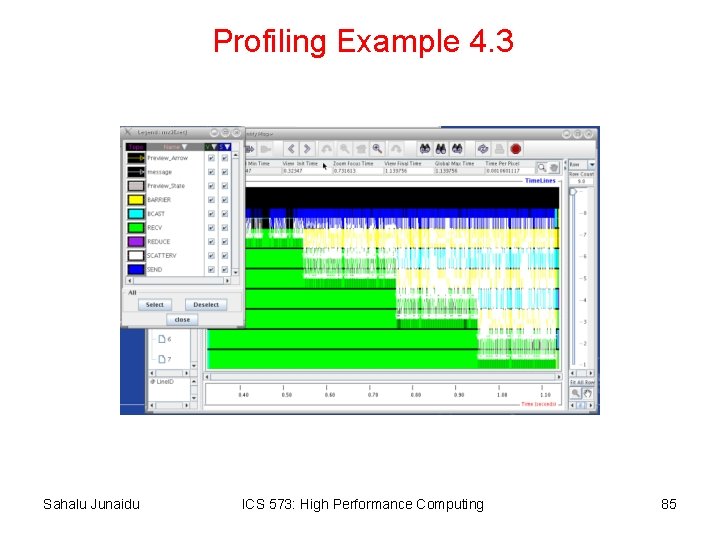
Profiling Example 4. 3 Sahalu Junaidu ICS 573: High Performance Computing 85

Example 5: Document Classification • MPI functions introduced in this example – – – MPI_Irecv – to initiate a nonblocking receive MPI_Isend – to initiate a nonblocking send MPI_Wait – to wait for a nonblocking communication to complete MPI_Probe – to check for an incoming message MPI_Get_count – to find the length of a message MPI_Testsome – to return information on all completed nonblocking communications Reading Assignment Sahalu Junaidu ICS 573: High Performance Computing 86