Moving Cash Flows Review Formulas Growing Annuity Annuities

Moving Cash Flows: Review

Formulas

Growing Annuity • Annuities are a constant cash flow over time • Growing annuities are a constant growth cash flow over time

What are you worth today? • You will make $100, 000 the first year. • You expect to work for 40 years, get 9% raises every year and 20% per year on investments.

Cash Flow Timing • When does the first cash flow occur relative to the present value of the _______ – Perpetuity? Growing perpetuity? – Annuity? Growing annuity? • One period later!

Review: Bond Features • Coupon Payments: Regular interest payments – Semi annual for most US corporate bonds – Types of Coupon payments • Fixed Rate: 8% per year • Floating Rate: 6 -mo. Treasury bill rate + 100 basis points. • Face or Par Value: $1, 000/bond • Maturity: no. of years from issue date until principal is paid • Coupon Rate

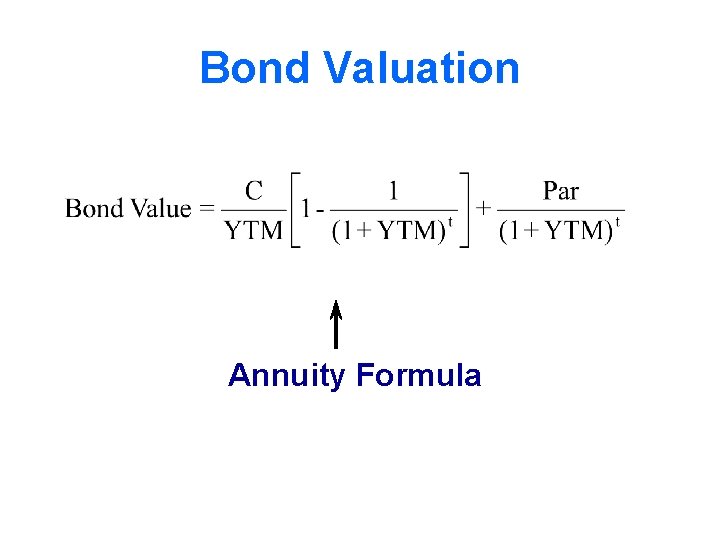
Bond Valuation Annuity Formula

What is the price of a $1000 bond maturing in ten years with a 12% coupon that is paid semiannually if the YTM is 10%

Stock Valuation

Common Stock Valuation is Difficult • Uncertain cash flows – Equity is the residual claim on the firm’s cash flows • Life of the firm is forever • Rate of return (the appropriate discount rate) is not easily observed

Differential Growth Dividend Model • Forecasted Dividends grow at a constant rate, g 1 for a certain number of years and then grow at a second growth rate, g 2. • Example: The dividend of a company was $1 yesterday. During the next 18 years the dividend will grow at 14% per year. After that the dividend will grow at 10% per year. What is the price of the stock if the required return is 15%?

The first dividend regime is a growing annuity The second dividend regime is a growing perpetuity

Now, we need to sum the two dividend regime values.

EPS and Dividends • Dividends (share repurchase) are a function of… – Ability to pay: Cash flow uncertainty – Decision to pay: Managerial uncertainty • Why does a manager retain earnings? – Has better investment opportunities than the shareholder – Makes a sub-optimal decision for the shareholder • What is a “better investment opportunity”? – Investment has a NPV>0

Value a firm that retains earnings? • Fundamental valuation equation: Sum of the discounted cash flows • First component: PV(no-growth earnings stream) – Remember EPS=Net income/Shareholders equity • Second component: PV of growth opportunities – Look for pricing shortcuts: perpetuity, annuity, etc. • Rule: As long as PV(GO) > 0, price increases

One Time Investment Opportunity • Firm expects $1 million in earnings in perpetuity without new investments. Firm has 100, 000 shares outstanding. Firm has investment opportunity at t=1 to invest $1 million in a project expected to increase future earnings by $210, 000 per year. The firm’s discount rate is 10%. What is the share price with and without the project?

Constant Growth, Constant Investing • Firm Q has EPS of $10 at the end of the first year and a dividend pay-out ratio of 40%, r. E = 16% and a return on investment of 20%. The firm takes advantage of its growth opportunities each year by investing retained earnings. • PV(GO) model – 1 st investment = 0. 6 × $10 = $6, which generates 0. 2 × $6 = $1. 20 – Per share PVGO 1 = -6 + (1. 20/0. 16) = $1. 50 (at t=1) – 2 nd investment = 0. 6 × $11. 20 = $6. 72, generating 0. 2 × $6. 72 = $1. 344 – Per share PVGO 2 = -6. 72 + (1. 344/0. 16) = $1. 68 (at t=2)

Constant Growth, Constant Investing (cont) • Relationship between PV(GO)’s? – 1. 68 = (1+g) × 1. 5 g=0. 12 • Is there an easier way to estimate g for this case? – G=ROI x Investment Rate=0. 2 x (1 -0. 4)=0. 12 • PVGO 0 = $1. 50 / (0. 16 - 0. 12) =$37. 50 • No-growth dividend value: $10/0. 16 = $62. 50 • P = $62. 50 + $37. 50 = $100

Constant Growth, Constant Investing (cont) • Can we price this firm a different way? – Since the investment grows at a constant rate we can immediately estimate g – Investment rate x ROI = 0. 6 × 20% = 12% • Then estimate PV(GO) as a growing perpetuity based on dividends rather than cash flow – D 1 / (r. E - g) = $4 / (0. 16 - 0. 12) = $100 • So the entire firm is worth $100

Another Example Firm X currently has expected earnings of $100, 000 per year in perpetuity. Firm X is switching its policy and wants to invest 20% of its earnings in projects with a 10% return. The discount rate is 18%. • No-growth price: P=$100, 000/0. 18 = $555, 555 • PV(GO) is a constant growth perpetuity – What’s g? g=Investment rate x ROI = 0. 2 × 10% = 2% – What is the first year’s investment cash flow? Invest $20, 000 and receive $2, 000 forever – -20, 000+(2, 000/0. 18)=-8888. 89 – PV(GO) = (-8, 888. 89)/(0. 18 -0. 02) = - 55, 555 • New Policy: P=$555, 555 - 55, 555 = $500, 000