Movimiento en una dimensin Curso de Fsica I

Movimiento en una dimensión Curso de Física I

Contenido Desplazamiento, velocidad y rapidez Velocidad instantánea Aceleración Movimiento con aceleración constante Caida libre

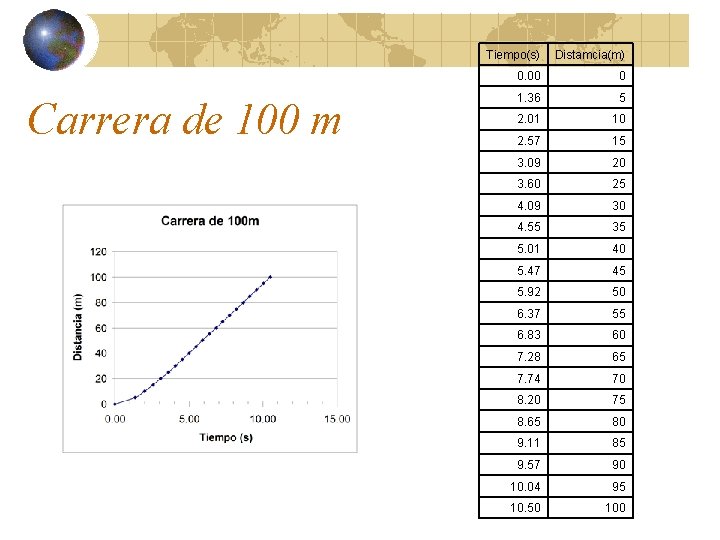
Carrera de 100 m Tiempo(s) Distamcia(m) 0. 00 0 1. 36 5 2. 01 10 2. 57 15 3. 09 20 3. 60 25 4. 09 30 4. 55 35 5. 01 40 5. 47 45 5. 92 50 6. 37 55 6. 83 60 7. 28 65 7. 74 70 8. 20 75 8. 65 80 9. 11 85 9. 57 90 10. 04 95 10. 50 100

Desplazamiento Se define el desplazamiento de una partícula que se mueve de una coordenada inicial xi a una coordenada final xf como: El desplazamiento puede ser positivo o negativo dependiendo de los signos y magnitudes de las coordenadas inicial y final. La distancia recorrida es la magnitud del desplazamiento. Para el corredor anterior algunos distancias recorridas son: Entre 0 y 2. 01 s es 10 – 0 = 10 m Entre 2. 01 y 4. 09 s es 30 – 10 = 20 m Entre 5. 01 y 10. 5 s es 100 – 50 = 50 m

Rapidez media La rapidez media es el cociente de la distancia total recorrida entre el intervalo de tiempo que toma en recorrerla. Para el corredor anterior: Entre 0 y 2. 01 s la rapidez es: 10/2. 01 = 4. 975 m/s Entre 2. 01 y 4. 09 s la rapidez es: (30– 10)/(4. 09– 2. 01) = 9. 615 m/s Entre 5. 01 y 10. 5 s la rapidez es: (100– 40)/(5. 01– 10. 5) = 10. 93 m/s

Velocidad La velocidad promedio es igual al desplazamiento total por intervalo de tiempo total: x(m) 3 x 2 1 La rapidez es la magnitud de la velocidad t 1 2 3 t(s) Movimiento de una partícula a velocidad constante.

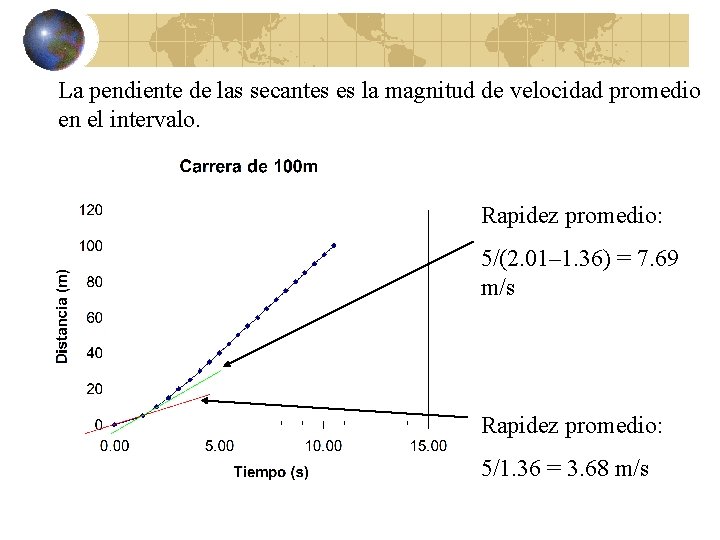
La pendiente de las secantes es la magnitud de velocidad promedio en el intervalo. Rapidez promedio: 5/(2. 01– 1. 36) = 7. 69 m/s Rapidez promedio: 5/1. 36 = 3. 68 m/s

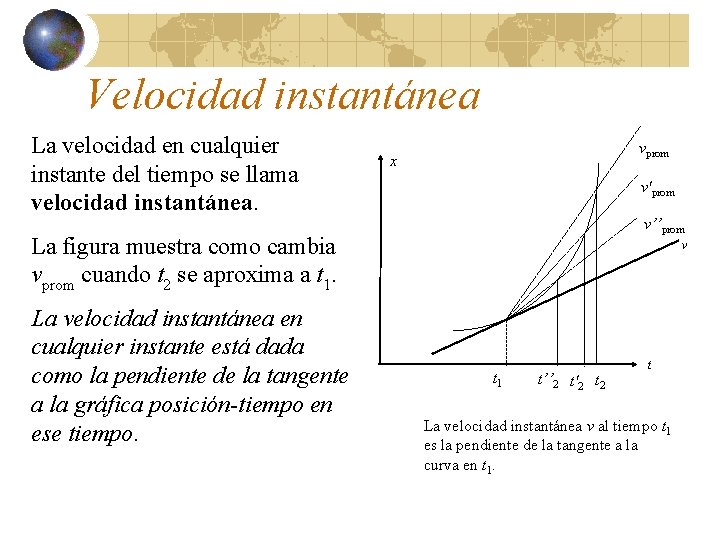
Velocidad instantánea La velocidad en cualquier instante del tiempo se llama velocidad instantánea. vprom x v'prom v’’prom La figura muestra como cambia vprom cuando t 2 se aproxima a t 1. La velocidad instantánea en cualquier instante está dada como la pendiente de la tangente a la gráfica posición-tiempo en ese tiempo. v t 1 t’’ 2 t'2 t La velocidad instantánea v al tiempo t 1 es la pendiente de la tangente a la curva en t 1.

Esto se expresa matemáticamente como x v=0 v>0 v<0 es decir, la velocidad instantánea es igual a la derivada de la posición respecto al tiempo. t La pendiente de la tangente puede encontrarse tomando dos puntos sobre la tangente. El signo de la velocidad instantánea indica la dirección del movimiento respecto al eje +x.

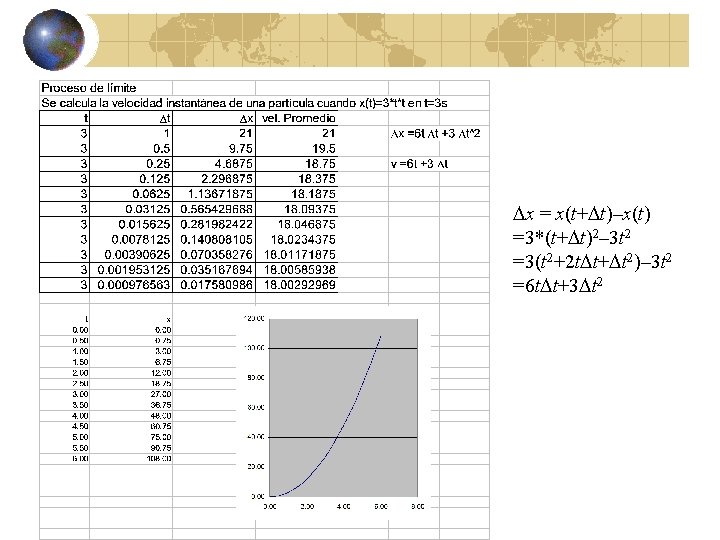
x = x(t+ t)–x(t) =3*(t+ t)2– 3 t 2 =3(t 2+2 t t+ t 2)– 3 t 2 =6 t t+3 t 2

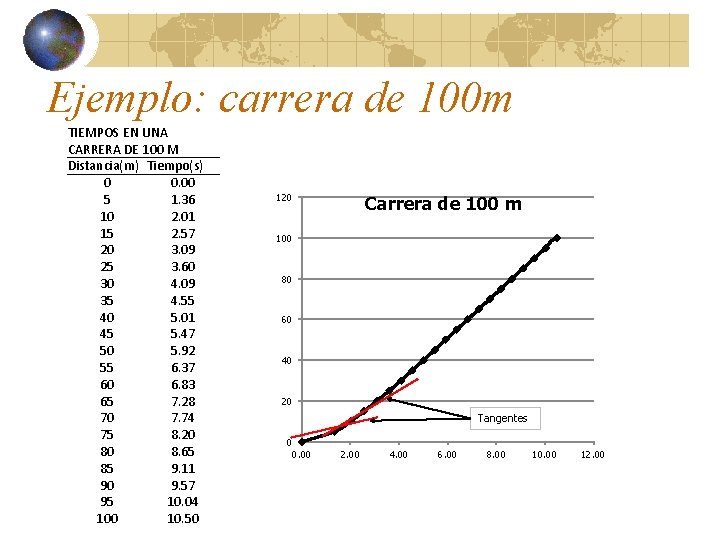
Ejemplo: carrera de 100 m TIEMPOS EN UNA CARRERA DE 100 M Distancia(m) Tiempo(s) 0 0. 00 5 1. 36 10 2. 01 15 2. 57 20 3. 09 25 3. 60 30 4. 09 35 4. 55 40 5. 01 45 5. 47 50 5. 92 55 6. 37 60 6. 83 65 7. 28 70 7. 74 75 8. 20 80 8. 65 85 9. 11 90 9. 57 95 10. 04 100 10. 50 120 Carrera de 100 m 100 80 60 40 20 Tangentes 0 0. 00 2. 00 4. 00 6. 00 8. 00 10. 00 12. 00

Tarea En 1971 Carl Lewis aventajó a Leroy Burrel en los campeonatos mundiales de Tokio, y estableció una nueva marca mundial de los 100 m planos. En la tabla de abajo aparecen los tiempos parciales de los dos, a intervalos de 10 m. Calcule la velocidad media de los dos competidores entre 0 y 50 m, 50 y 100 m, y 0 y 100 m. Calcule la velocidad media de cada uno a los 50 m tomando los valores para 40 m y 60 m. Distancia(m) 10 20 30 40 50 60 70 80 90 100 Tiempo(s) Lewis Burrel 1. 88 1. 83 2. 96 2. 89 3. 88 3. 79 4. 77 4. 68 5. 61 5. 55 6. 46 6. 41 7. 30 7. 28 8. 13 8. 12 9. 00 9. 01 9. 86 9. 88

Aceleración La aceleración promedio en un intervalo finito de tiempo se define como La aceleración tiene unidades de velocidad divididas por unidades de tiempo, o sea, unidades de longitud por (tiempo)2. La acelearción instantanea se define como:

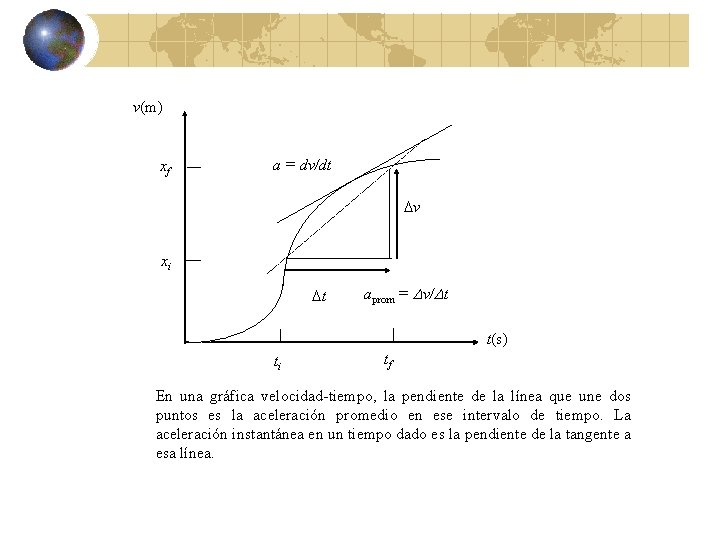
v(m) xf a = dv/dt v xi t aprom = Dv/Dt t(s) ti tf En una gráfica velocidad-tiempo, la pendiente de la línea que une dos puntos es la aceleración promedio en ese intervalo de tiempo. La aceleración instantánea en un tiempo dado es la pendiente de la tangente a esa línea.

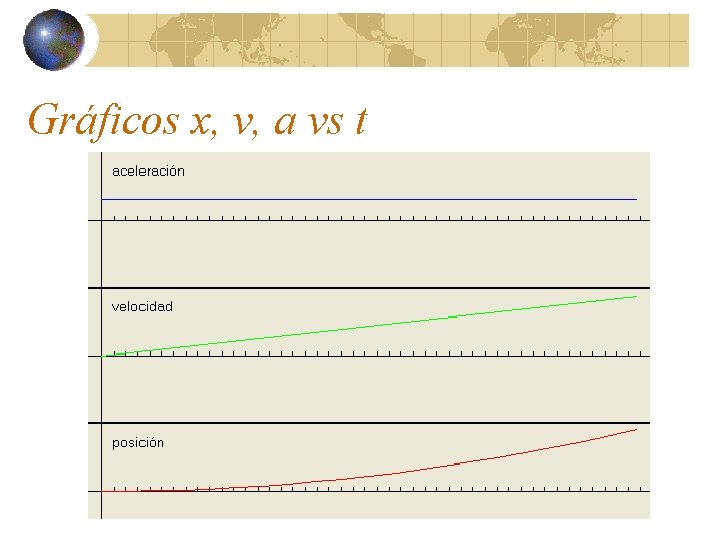
Graficos de x, v y a

Ejemplo Un automóvil en muy mal estado solo puede acelerar hacia adelante a una tasa constante de 0. 5 m/s 2. ¿Qué distancia deberá recorrer para alcanzar las 50 mi/hr? vf = 50 mi/hr = (50 mi/hr)(1609 m/mi)(1 hr/3600 s) = 22. 35 m/s tf = vf /a = (22. 35 m/s)/(0. 5 m/s 2) = 44. 69 s Con la velocidad promedio podemos calcular la distancia recorrida. En este caso la velocidad promedio es vp = (vf + vi)/2 = vf /2 xf = vp tf = (vf /2) tf = (22. 35/2 m/s)(44. 69 s) = 499. 41 m

Gráficos x, v, a vs t

Una corredora de 100 m acelera hasta llegar a 10 m/s a los 4 s de haber arrancado, mantiene es velocidad hasta los 8 s, y cuando sabe que va a ganar desacelera hasta 8 m/s hasta el final de la carrera, que dura 12. 7 s. ¿Cua´es la aceleración media en cada intervalo?

Tarea 5. Obtenga la aceleración media en cada uno de los siguientes casos: a) un avión Jumbo DC 10 parte del reposo y alcanza su velocidad de despegue a 360 km/h en 50 s; 1. b) un avión jet Corsair naval llega a un portaaviones a 180 km/h y llega al reposo en 4 s por una red; 2. c) un cohete alcanza 1440 km/h en 2 s. 3. d) Un estudiante alcanza los 8 m/s en 3 s.

Movimiento con aceleración Además, se cumple que constante Si la aceleración es constante se pueden hacer las siguientes simplificaciones: (2) De (1) y (2) con x = xo en t = 0 (3) De (1) y (3) Si en ti = 0 v = vo, entonces o (4) (1) Eliminando t en (1) y (3) (5)

Ecuaciones de cinemática

Ejemplo Un nuño rueda una pelota de hule en un corredor alfombrado. Le imprime una velocidad inicial de 2 m/s, y la alfombra lo desacelera de forma constante a 0. 2 m/s 2. ¿Qué distancia recorre antes de detenerse y cuanto tiempo le toma detenerse? Datos v 0 = 2 m/s a = – 0. 2 m/s 2 v = 0. 0 m/s Para encontrar la distancia podemos usar Para encontrar el tiempo podemos usar 0 = (2 m/s)+ (-0. 2 m/s 2)t t = 10 s 0 = (2 m/s)2+ 2(– 0. 2 m/s 2)(x – 0 m) x = 10 m

Tarea Un automóvil viaja a 25 mi/h, y debe alcanzar como mínimo 45 mi/h en un carril de acceso de 300 m. ¿Cuál debe ser la aceleración constante del vehículo?

Caida libre La caída libre de un cuerpo es un caso de movimiento con aceleración constante. Las ecuaciones que describen este movimiento son Donde g = 9. 8 m/s 2.

Ejemplo ¿Cuánto tiempo tarde en caer una pelota desde una altura de 100 m? ¿Cuál es la velocidad de la pelota al momento de tocar el suelo? 0 – 100 = (0 m/s)t – ½(9. 8 m/s 2)t 2 Datos t = 4. 52 s v 0 = 0 m/s Para encontrar v usamos: y 0 = 100 m y=0 m Usamos: v = 0 m/s – (9. 8 m/s 2)(4. 52 s) = – 44. 3 m/s

Ejemplo En el ejemplo anterior ¿qué tiempo tarda en caer de 100 m a 75 m? ¿de 75 m a 50 m? ¿de 50 m a 25 m? ¿de 25 m a 0 m? Usamos: De 100 a 75 De 100 a 50 De 100 a 25 De 100 a 0 Las diferencias son: De 100 a 75 De 75 a 50 De 50 a 25 De 25 a 0 t 2 = 2(100 m – 75 m)/(9. 8 m/s 2) = 5. 10 s 2 t = 2. 26 s t = 3. 19 s t = 3. 91 s t = 4. 52 s t = 2. 26 s t = 0. 93 s t = 0. 72 s t = 0. 61 s

Ejemplo En el ejemplo anterior ¿Cuáles son las posiciones de la pelota en t igual a 1 s, 2 s, 3 s y 4 s? Usamos: Con y = 75 m, 50 m y 25 m y y 0 = 100 m t=1 y = (100 m) + (– 9. 8 m/s 2)(1 s) 2/2 = 95. 1 m t=2 y = (100 m) + (– 9. 8 m/s 2)(2 s) 2/2 = 80. 4 m t=3 y = (100 m) + (– 9. 8 m/s 2)(3 s) 2/2 = 55. 9 m t=4 y = (100 m) + (– 9. 8 m/s 2)(4 s) 2/2 = 21. 6 m

Ejemplo Una flecha disparada verticalmente hacia arriba toca tierra 8 s más tarde. Halle: (a) su máxima altitud; (b) su velocidad inicial. La flecha subió durante 4 s y bajo en los 4 s restantes. En 4 s un objeto cae h = (9. 8 m/s 2)(4 s) 2/2 = 78. 4 m La velocidad que adquiere es v = 0 m/s – (9. 8 m/s 2)(4. 0 s) = – 39. 2 m/s La velocidad inicial es de igual magnitud

Tarea Una pelota de tenis es arrojada desde una altura de 5 m y rebota a una altura de 3. 2 m. Si esta en contacto con el piso durante 0. 036 s, ¿Cuál es su aceleración promedio durante ese periodo?