Movimiento Ejercitacin Objetivos Aplicar conceptos como distancia recorrida

Movimiento Ejercitación

Objetivos Aplicar conceptos como “distancia recorrida”, “desplazamiento”, “trayectoria”, “vector”, a la resolución de problemas.

Ejemplos 1. La persona d la imagen se mueve en línea recta, partiendo desde A hasta B, luego de B a C, luego de C a D y, por último, de D a E. Determine: a) Distancia total recorrida b) Desplazamiento total (dibuje el vector) c) El desplazamiento de A a D D 4 m A 2 m C 3 m B 5 m E

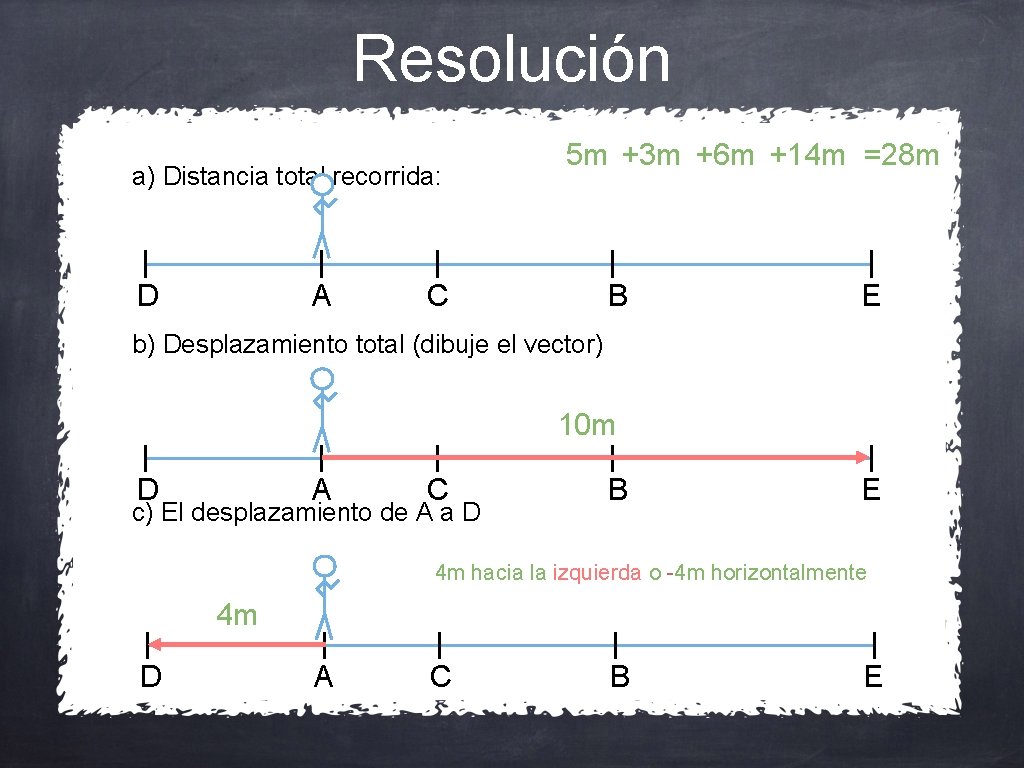
Resolución a) Distancia total recorrida: D A 5 m +3 m +6 m +14 m =28 m C B E b) Desplazamiento total (dibuje el vector) 10 m D A C c) El desplazamiento de A a D B E 4 m hacia la izquierda o -4 m horizontalmente 4 m D A C B E

Ejercicios 1. Si ahora la persona parte en B, luego pasa a C, luego a D, después a A y, finalmente, a E, ¿cuál sería la/el a) distancia total recorrida? 13[m] b) desplazamiento total (dibuje el vector) 5[m] c) desplazamiento de A a D 4[m] D 4 m A 2 m C 3 m B 5 m E

Ejemplos 2. ¿Qué ocurriría con el desplazamiento si, el movimiento es, por ejemplo, en una diagonal? . Para analizar lo que ocurre, observe el diagrama que muestra el recorrido de una persona que parte en A, pasa por B y luego C siendo A, B y C, los vértices de un “triángulo rectángulo”. A 4 m 5 m B 3 m C * ¿Cuánto vale la distancia total recorrida? *¿Cuánto vale el desplazamiento total experimentado por la persona?

Ejemplos Respuesta 2: * ¿Cuánto vale la distancia total recorrida? Sumo los 4[m] de A a B con los 3[m] de B a C. 7[m] en total *¿Cuánto vale el desplazamiento total experimentado por la persona? Se dibuja el vector desplazamiento AC indicando su magnitud: 5[m] (se calcula con Pitágoras pues ΔABC es rectángulo) A 4 m 5 m B 3 m C 5 m Desplazamiento Debe indicarse: magnitud, dirección y sentido.

Ejemplos 3. Por supuesto, con un triángulo de otras dimensiones, ocurre lo mismo. ¡La magnitud del desplazamiento no tiene por qué ser un número entero! y la dirección y el sentido pueden ser cualquiera. A 7 m 85 m B 6 m C * ¿Cuánto vale la distancia total recorrida? *¿Cuánto vale el desplazamiento total experimentado por la persona?

Ejemplos Respuesta 3: * ¿Cuánto vale la distancia total recorrida? Sumo los 7[m] de A a B con los 6[m] de B a C. 13[m] en total *¿Cuánto vale el desplazamiento total experimentado por la persona? Se dibuja el vector desplazamiento AC indicando su magnitud: Pitágoras pues ΔABC es rectángulo) . (se calcula con 85 m A 7 m 85 m B 85 m 6 m C Desplazamiento Debe indicarse: magnitud, dirección y sentido.

Ejercicios 4. Y si, en el ejemplo 1, la persona volviera al punto A luego de pasar por C, ¿Cuáles serían los valores del desplazamiento y la distancia total recorridas? A 4 m 5 m B 3 m C * ¿Cuánto vale la distancia total recorrida? *¿Cuánto vale el desplazamiento total experimentado por la persona?

Ejemplos Respuesta 2: * ¿Cuánto vale la distancia total recorrida? Sumo los 7[m] recorridos antes, más los 5[m] de C a A; 12[m] *¿Cuánto vale el desplazamiento total experimentado por la persona? Como vuelve al inicio, el punto de partida y final son el mismo, por lo tanto el desplazamiento es cero. A 4 m 5 m B 3 m C