Movimento Circular Uniforme v 1 Movimento Circular Uniforme

Movimento Circular Uniforme

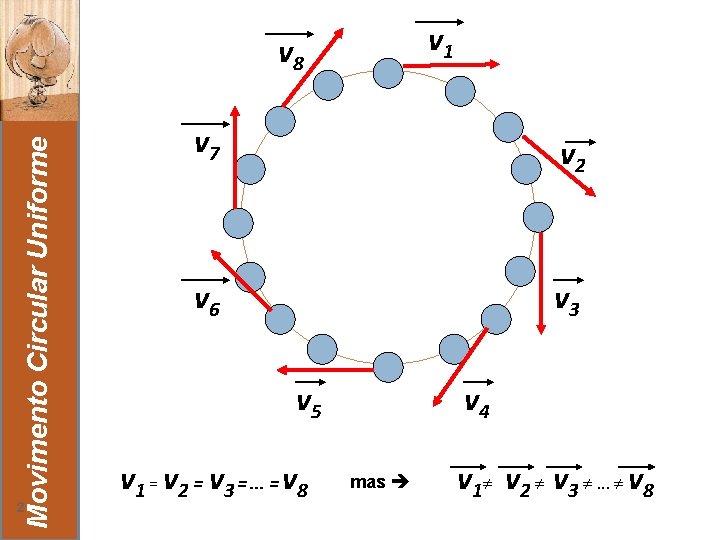
v 1 Movimento Circular Uniforme v 8 2 v 7 v 2 v 6 v 3 v 5 v 1 = v 2 = v 3 =. . . = v 8 v 4 mas v 1 v 2 v 3 . . . v 8

Período (T) : tempo para que ocorra uma volta completa. Período e Frequência unidades: segundo (SI), minutos, horas, etc 3 Frequência (f) : número de voltas na unidade de tempo. unidades: voltas por segundo Hertz (HZ) (SI) rotações por minuto (rpm) Exemplo 1 Um ponto na periferia de um disco numa vitrola dá 495 voltas em 15 minutos. Determine, em minutos e rpm, o período e a frequência deste movimento.

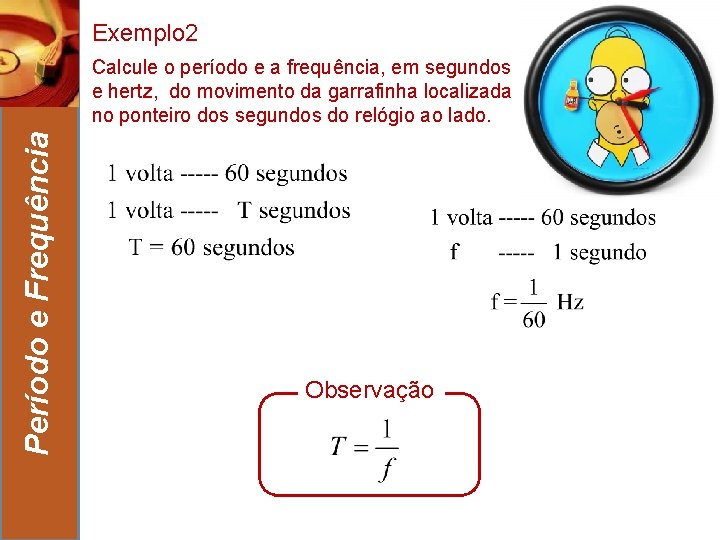
Exemplo 2 Período e Frequência Calcule o período e a frequência, em segundos e hertz, do movimento da garrafinha localizada no ponteiro dos segundos do relógio ao lado. 4 Observação

Exemplo 3 Período e Frequência Uma das atrações típicas do circo é o equilibrista sobre monociclo. 5 O raio da roda do monociclo utilizado é igual a 20 cm, e o movimento do equilibrista é retilíneo. O equilibrista percorre, no início de sua apresentação, uma distância de 24 metros. Determine o número de pedaladas, por segundo, necessárias para que ele percorra essa distância em 30 s, considerando o movimento uniforme.

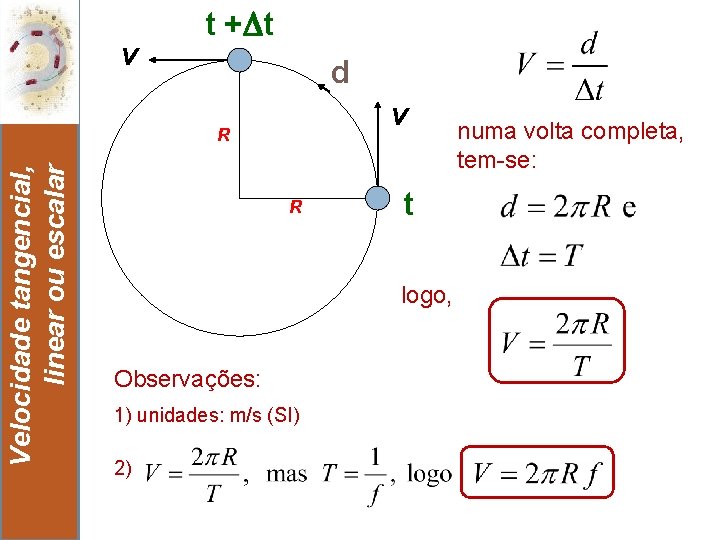
v t + t d v Velocidade tangencial, linear ou escalar R 6 R t logo, Observações: 1) unidades: m/s (SI) 2) numa volta completa, tem-se:

Velocidade tangencial, linear ou escalar Exemplo 7 (Fuvest) Um farol marítimo projeta um facho de luz contínuo, enquanto gira em torno do seu eixo à razão de 10 rotações por minuto. Um navio, com o costado perpendicular ao facho, está parado a 6 km do farol. Com que velocidade um raio luminoso varre o costado do navio? a) 60 m/s b) 60 km/s c) 6, 3 km/s X d) 630 m/s e) 1, 0 km/s

(em radianos) O que é o radiano numa volta completa (360º), em qualquer circunferência, tem-se: (graus) (radianos) 360º 2 180º 90º 60º 45º 30º 8

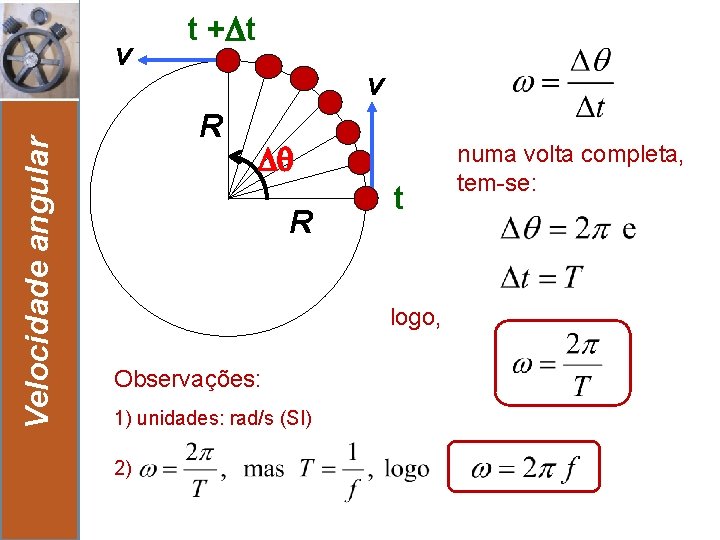
Velocidade angular v v R R t logo, Observações: 1) unidades: rad/s (SI) 2) 9 t + t numa volta completa, tem-se:

Velocidade angular Exemplo 1 10 (Uel) Um ciclista percorre uma pista circular de raio igual a 20 m, fazendo um quarto de volta a cada 5, 0 s. Para esse movimento, a freqüência em Hz, e a velocidade angular em rad/s são, respectivamente a) 0, 05 e /5 b) 0, 05 e /10 X c) 0, 25 e /5 d) 4, 0 e /5 e) 4, 0 e /10 significa que a cada segundo o ciclista varre um ângulo de 18º.

Velocidade angular Exemplo 2 11 (Uel) Um antigo relógio de bolso tem a forma mostrada na figura a seguir, com o ponteiro dos segundos separado dos outros dois. A velocidade angular do ponteiro dos segundos, cujo comprimento é 0, 50 cm, em rad/s, e a velocidade linear de um ponto na extremidade de tal ponteiro, em cm/s, são respectivamente, iguais a a) 2 e b) 2 e 4 c) /30 e /15 d) /30 e /60 X e) /60 e 2

Relação entre V e 12 Exemplo ( PUC-RIO) Um ciclista pedala em uma trajetória circular de raio R = 5 m, com a velocidade de translação v = 150 m/min. A velocidade angular do ciclista em rad/min é: a) 60 b) 50 c) 40 d) 30 e) 20

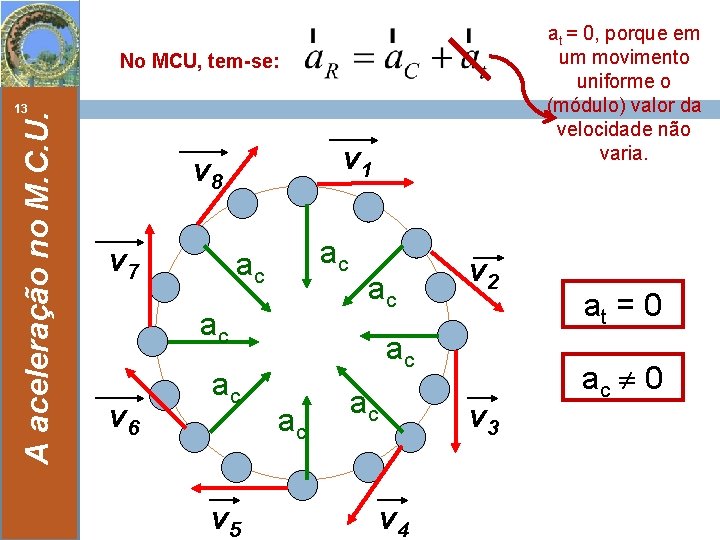
at = 0, porque em um movimento uniforme o (módulo) valor da velocidade não varia. No MCU, tem-se: A aceleração no M. C. U. 13 v 1 v 8 v 7 ac ac ac v 6 ac v 5 ac v 2 ac ac ac v 3 v 4 at = 0 ac 0

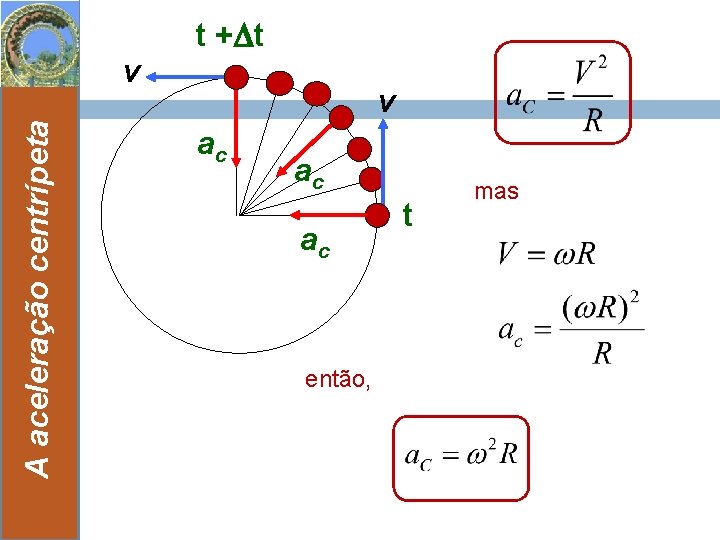
t + t v v A aceleração centrípeta 14 ac ac ac então, t mas

Exemplo 1 Aceleração centrípeta 15 Um móvel realiza um movimento circular e uniforme, com velocidade de 5 m/s. Sendo a aceleração centrípeta igual a 10 m/s 2, determine o raio de sua trajetória. Exemplo 2 (FEI) Uma automóvel realiza uma curva de raio 20 m com velocidade constante de 72 km/h. Qual é a sua aceleração durante a curva? a) 0 m/s 2 b) 5 m/s 2 c) 10 m/s 2 d) 20 m/s 2 X e) 3, 6 m/s 2

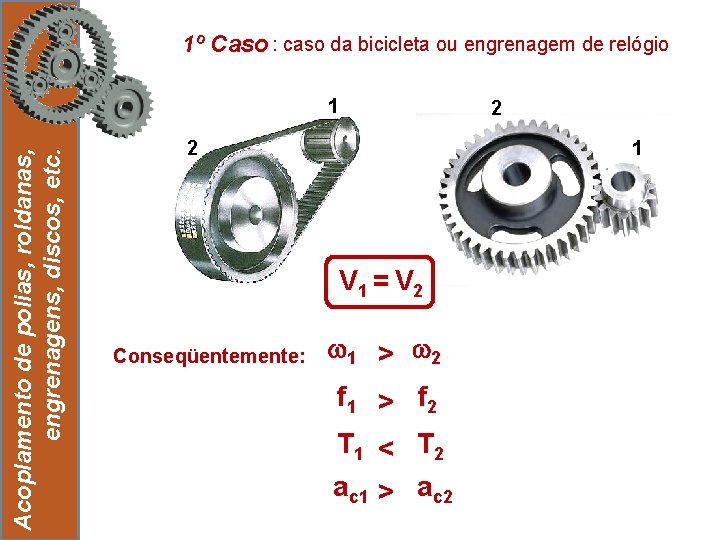
1º Caso : caso da bicicleta ou engrenagem de relógio Acoplamento de polias, roldanas, engrenagens, discos, etc. 1 16 2 2 1 V 1 = V 2 Conseqüentemente: 1 > 2 f 1 > f 2 T 1 < T 2 ac 1 > ac 2

Acoplamento de polias, roldanas, engrenagens, discos, etc. 17 (vídeo 1)

Acoplamento de polias, roldanas, engrenagens, discos, etc. 18 (vídeo 2)

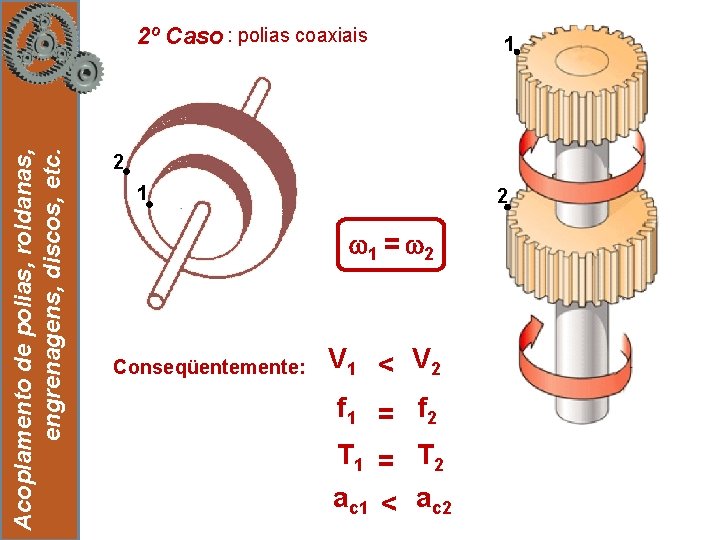
Acoplamento de polias, roldanas, engrenagens, discos, etc. 2º Caso : polias coaxiais 19 1 2 1 = 2 Conseqüentemente: V 1 < V 2 f 1 = f 2 T 1 = T 2 ac 1 < ac 2

Velocidade angular Exemplo 1 20 As polias indicadas na figura se movimentam em rotação uniforme, ligadas por um eixo fixo. Sabendo que a velocidade angular da polia A é 8 rad/s e que o Raio de A é 80 cm e o Raio de B é 40 cm, calcule: a) A velocidade escalar de um ponto da periferia da polia B; b) A aceleração centrípeta de um ponto da periferia da polia A.

Velocidade angular Exemplo 2 21 Duas polias de raios a e b estão acopladas entre si por meio de uma correia, como mostra a figura adiante. A polia maior, de raio a, gira em torno de seu eixo levando um tempo T para completar uma volta. Supondo que não haja deslizamento entre as polias e a correia, calcule: a) O módulo V da velocidade do ponto P da correia. b) O tempo t que a polia menor leva para dar uma volta completa.

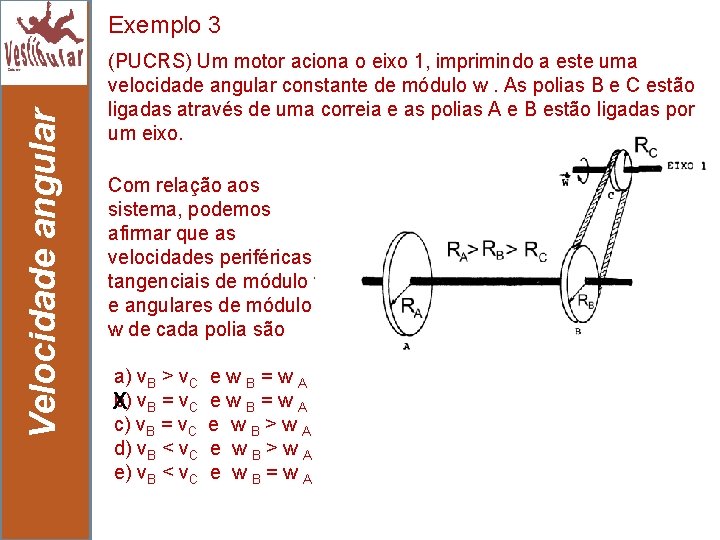
Velocidade angular Exemplo 3 22 (PUCRS) Um motor aciona o eixo 1, imprimindo a este uma velocidade angular constante de módulo w. As polias B e C estão ligadas através de uma correia e as polias A e B estão ligadas por um eixo. Com relação aos sistema, podemos afirmar que as velocidades periféricas tangenciais de módulo v e angulares de módulo w de cada polia são a) v. B > v. C b) v. B = v. C X c) v. B = v. C d) v. B < v. C ew. B=w. A e w. B>w. A e w. B=w. A

Velocidade angular Exemplo 4 23 Para dar o efeito da saia rodada, o figurinista da escola de samba coloca sob as saias das baianas uma armação formada por três tubos plásticos, paralelos e em forma de bambolês, com raios aproximadamente iguais a r� 1 = 0, 50 m, r 2 = 0, 75 m e r 3 = 1, 20 m. Pode-se afirmar que, quando a baiana roda, a relação entre as velocidades angulares ( ) respectivas aos bambolês 1, 2 e 3 é a) 1 � > 2 > 3. b) 1 < 2 < 3. c) 1 = 2 = 3. X d) 1 � = 2 > 3. e) 1 � > 2 = 3.

Velocidade angular Exemplo 5 24 (UFPE) A polia A' de raio r‘A=12 cm é concêntrica à polia A, de raio r. A=30 cm , e está rigidamente presa a ela. A polia A é acoplada a uma terceira polia B de raio r. B=20 cm pela correia C, conforme indicado na figura. Qual deve ser o raio da polia B', concêntrica a B e rigidamente presa a ela, de modo que A' e B' possam ser conectadas por uma outra correia C', sem que ocorra deslizamento das correias?