Mountain Video Showed video of mountain landscape generated

Mountain Video Showed video of mountain landscape generated by the 4 k file on this page: http: //pouet. net/prod. php? which=52938

A Random Talk About Random Dave Feinberg

Which has more information? n n The outcome of 2 coin flips: heads The outcome of 3 coin flips: tails heads

Which has more information? n n n The outcome of 10 coin flips: "HHTTHTHTTT" A strand of 10 DNA bases: "ATTGACATGG" 10 decimal digits: "7523104698"

Units of Information n n bit = binary digit a single "0" or "1" outcome of 1 binary decision like a coin flip ten coin flips -> ten bits

Bits n n How many bits do I need to store the outcome of one home pregnancy test? A home pregnancy test reveals 1 bit of information. It may be the most important life-changing bit of information, but it's still just 1 bit.

One Itty Bitty Guy

Representing in Binary n "HHTTHTHTTT" n "H" = 0 "T" = 1 n 0011010111 n n How can we represent "ATTGACATGG" in binary?

Representing in Binary n n n n 2 bits to represent 1 DNA base "A" = 00 "C" = 01 "G" = 10 "T" = 11 ATTGACATGG 00111110000100111010 How many bits?

Representing in Binary n bits per symbol = log 2(possible symbols) n 4 symbols: ACGT n log 24 = 2 bits per symbol

Representing in Binary n n n How much information in "7523104698"? 10 possible symbols log 210 = approx 3. 32 bits per symbol 10 decimal digits = approx 33. 2 bits Bogus! How many bits does it really take to represent 10 possible symbols?

decimal digits in 4 bits each n 0 1 2 3 4 n Seems wasteful. Can we do better? n n = = = 0000 0001 0010 0011 0100 5 6 7 8 9 = = = 0101 0110 0111 1000 1001

decimal digit = 3 or 4 bits n n n n 0 1 2 3 4 = = = 000 001 010 011 100 5 6 7 8 9 = = = 101 1100 1101 1110 1111 What number is "0101011100"? On average: 3. 4 bits per digit.

Which contains most information? n Outcome of 6 coin flips: "HHTHTT" n 3 DNA bases: "ATG" n 2 decimal digits: "74"

Information n more bits = more information n Right?

Memorizing Volunteer to memorize 8 bits n 00011110 Volunteer to memorize 50 bits n 0000000000000000000 Which is easier to memorize? Which contains more information?

Memorizing n 0000000000000000000000 Another volunteer to memorize 50 bits n 0010001110100110110001010001010100 1111001 Which is easier to memorize? Which contains more information? Why?

Information: another definition n Amount of information = length of shortest program that outputs those bits.

Write a program to print 0000000000000000 for i in range(50): print "0",

Write a program to print 0010001110100110110001 0100010101001111001 print "0010001110100110110001 0100010101001111001"

Memorizing Programs print "0010001110100110110001 0100010101001111001" is harder to memorize than for i in range(50): print "0",

Therefore 0010001110100110110001 0100010101001111001 contains more information than 0000000000000000

Information n More random = more information

Pi and Information n n 3. 14159265358979323846264338327. . . How much information is stored in the digits of pi?

Calculating Pi n pi = 4/1 - 4/3 + 4/5 - 4/7 +. . .

Calculating Pi sign = 1 n=1 pi = 0 while True: pi = pi + sign * 4. 0 / n print pi sign = 0 - sign n=n+2

Information in Pi n n n The digits of pi are output by a short program. Therefore, pi does not contain very much information. (Then what does? ? ? )

Programs That Print Numbers Write a program to print 0. 1 print "0. 1"

Programs That Print Numbers Write a program to print 0. 11111. . . print "0. ", while True: print "1",

Programs That Print Numbers Write a program to print 0. 121212. . . print "0. ", while True: print "12",

Programs That Print Numbers Write a program to print 0. 1211211112111112. . . print "0. ", ones = 1 while True: for i in range(ones): print "1", ones = ones + 1 print "2",

Programs That Print Numbers n n Although 0. 121121112. . . requires an infinite number of decimal digits, It can be printed by a program of finite length.

Programs That Print Numbers n n Are there any numbers that cannot be printed by a computer program? Yes!

Programs That Print Numbers n n n A number that can be printed by a computer program is called a computable number. A number that cannot be printed by a computer program is called an uncomputable number. Are there a lot of uncomputable numbers?

The Number Line n n n If I point to a random point on the number line, what is the probability that I will point to an integer? A rational (fraction)? A computable number? -1 0 1 2

Information and Science n n n more random = more information. randomness = disorder. In science, what do we usually call the measure of the amount of disorder in a system? information = randomness = disorder = entropy 2 nd Law of Thermodynamics: In a system, a process that occurs will tend to increase the total entropy of the universe. Does this tell us anything about information?

Something Different. . . n n We'll come back to random/information. . . Let's make some pictures

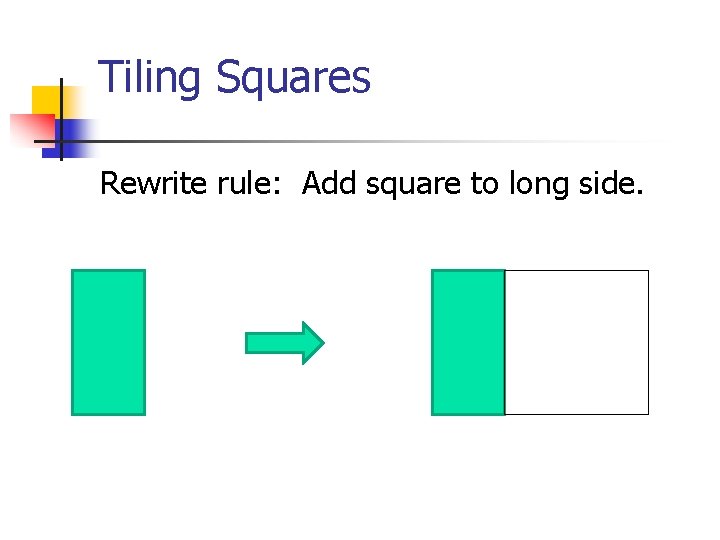
Tiling Squares Rewrite rule: Add square to long side.

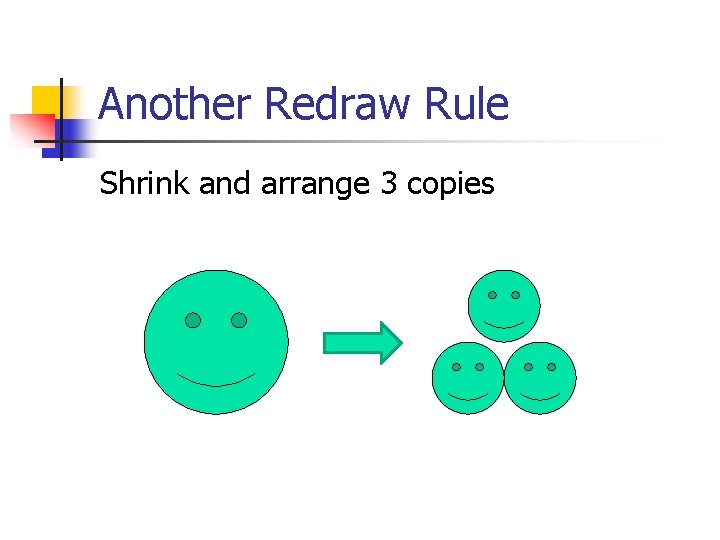
Another Redraw Rule Shrink and arrange 3 copies

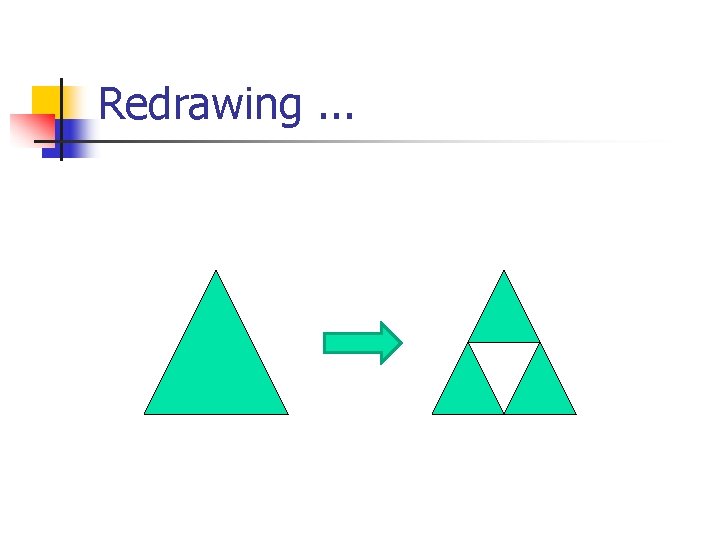
Redrawing. . .

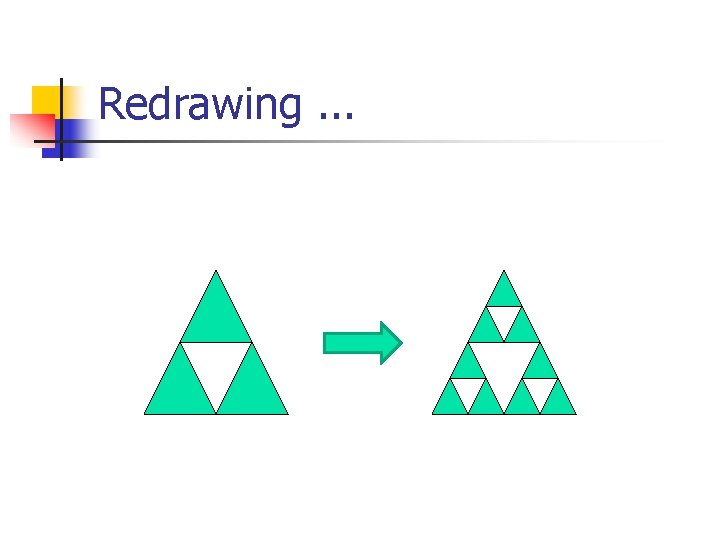
Redrawing. . .

Redrawing. . .

Redrawing. . .

Redrawing. . .

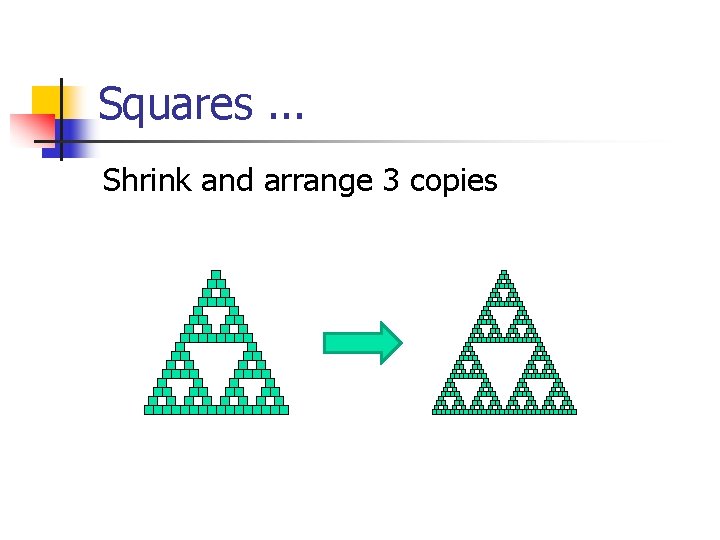
Fractals n n n A fractal is: "a rough or fragmented geometric shape that can be split into parts, each of which is (at least approximately) a reduced-size copy of the whole"--a property called self-similarity. --Wikipedia Fractals are recursive structures.

Triangles? n Why is the sierpinski triangle full of little triangles? Where did the triangles come from?

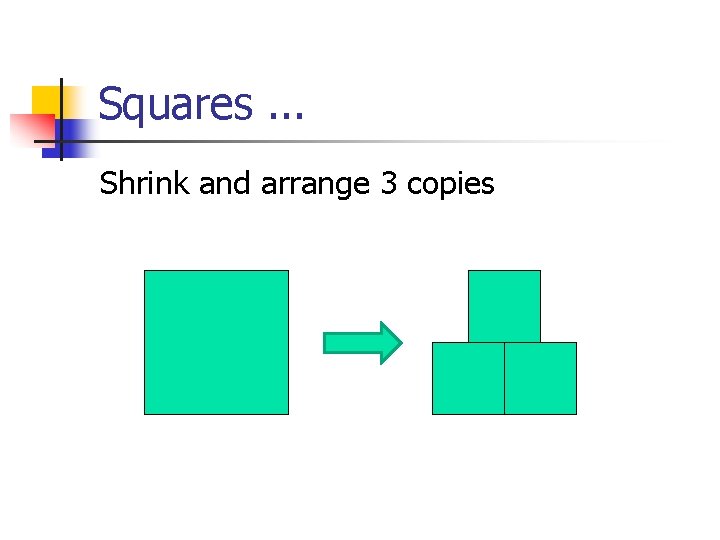
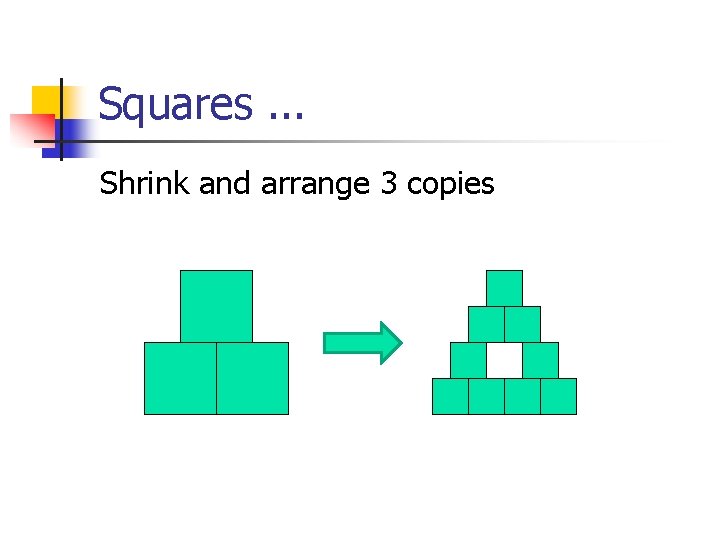
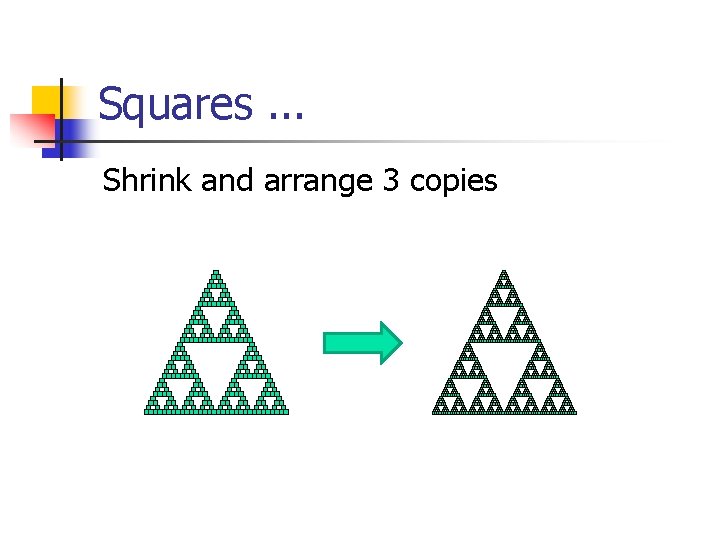
Squares. . . Shrink and arrange 3 copies

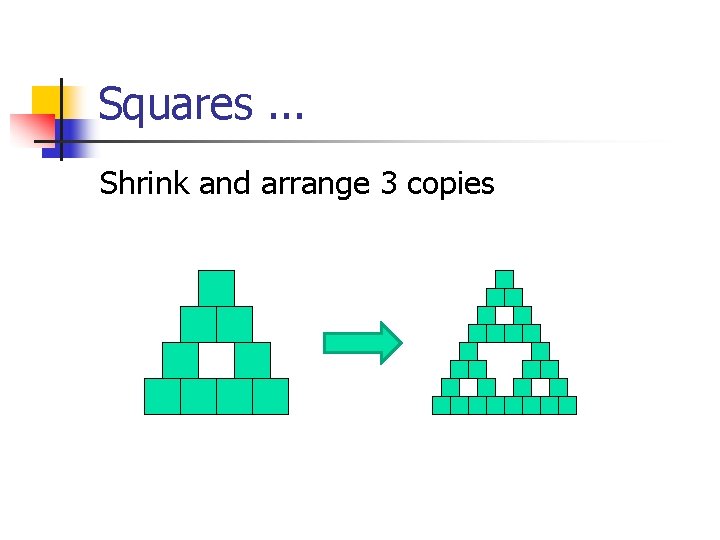
Squares. . . Shrink and arrange 3 copies

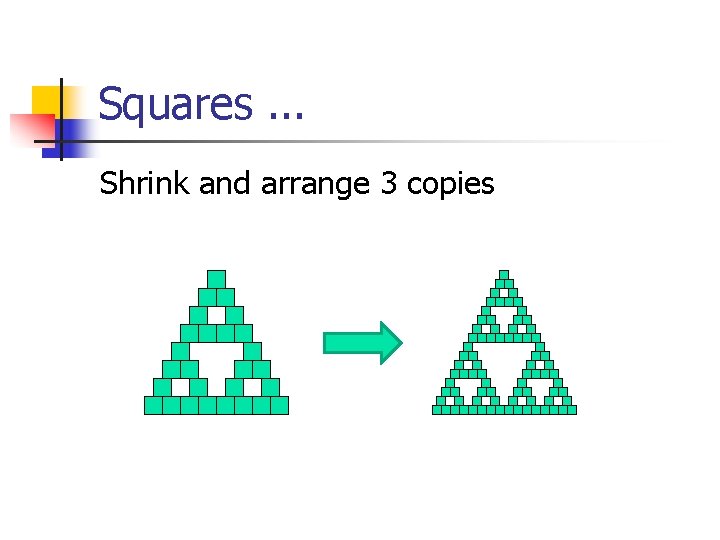
Squares. . . Shrink and arrange 3 copies

Squares. . . Shrink and arrange 3 copies

Squares. . . Shrink and arrange 3 copies

Squares. . . Shrink and arrange 3 copies

Fractal Antennas n n (Gratuitous connection to science) Some self similar fractal shapes have a property of "frequency invariance"—the same electromagnetic properties no matter what the frequency. --Wikipedia

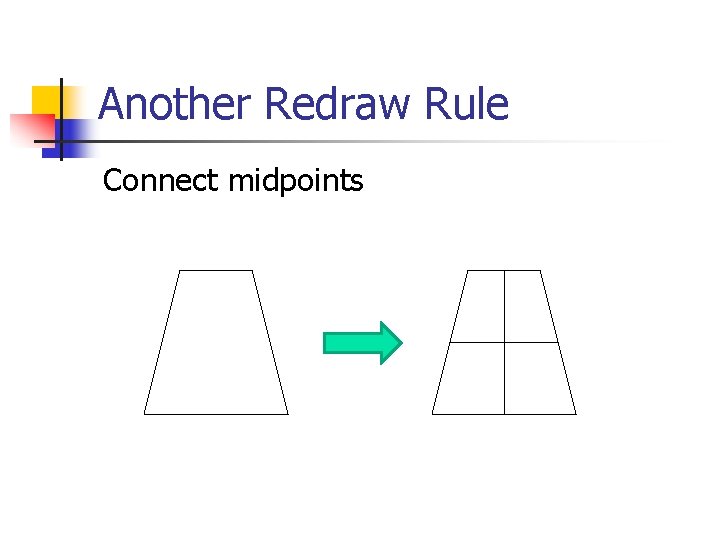
Another Redraw Rule Connect midpoints

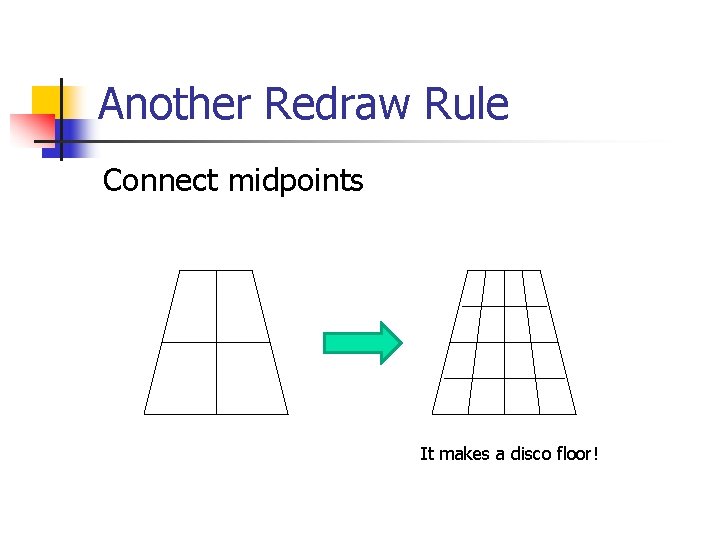
Another Redraw Rule Connect midpoints It makes a disco floor!

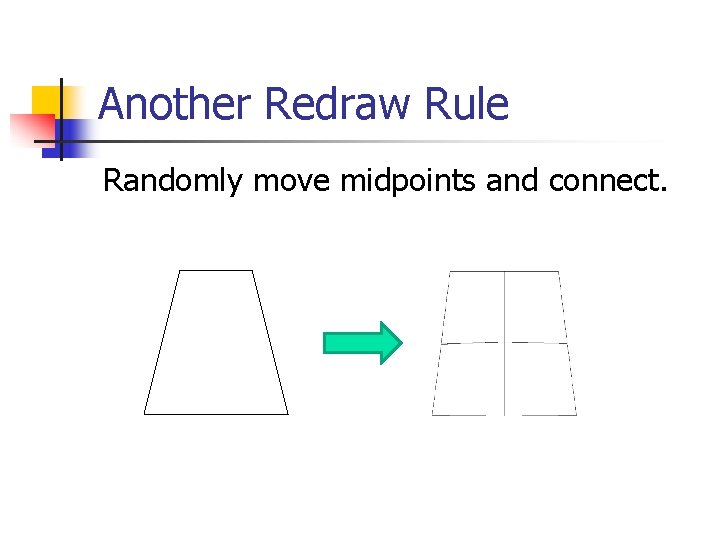
Another Redraw Rule Randomly move midpoints and connect.

Another Redraw Rule Randomly move midpoints and connect.

Another Redraw Rule Randomly move midpoints and connect.

Another Redraw Rule Randomly move midpoints and connect.

Another Redraw Rule Randomly move midpoints and connect.

Another Redraw Rule What does this look like?

Mountains I Generated

Connections Approximate fractals are easily found in nature. These objects display self-similar structure over an extended, but finite, scale range. Examples include clouds, snow flakes, crystals, mountain ranges, lightning, river networks, cauliflower or broccoli, systems of blood vessels and pulmonary vessels, coastlines, tree branches, galaxies, etc. (borrowed from Wikipedia)

Fractals n n All these natural phenomena are fractallike. What does that tell us about nature?

Sandwich Video http: //www. colbertnation. com/the-colbert -report-videos/340908/july-072010/thought-for-food---kentucky-tuna--grilled-cheese-burger-melt Started at 4: 50. (Not everything earlier is appropriate. )

The Mountain Video n n n Was produced from somebody's 4 kilobyte computer program. How large is 4 kilobytes? Is there a lot of information in that video?

Determinism n n n The computer is deterministic. Follows rules, step by step. Does that mean a program does the same thing every time, given the same input? Can a computer behave randomly?

Cellular Automata n A kind of toy universe. n Download and run: Cellular. Automata. jar n Try running "rule 18" one generation at a time. Can you tell what it's doing?

Rule 18 n n For each cell, look at the 3 cells on the row immediately above it (immediately above, above-and-to-the-left, and above -and-to-the-right). If the middle is white and either the left or the right is black (but not both), then this cell will become black. Otherwise, it will be white.

Now You Try n n On a sheet of graph paper, put a black mark in the middle square along the top of the page. This top row is the first generation. Use the rule to fill in the black marks for the 2 nd generation, 3 rd generation, and so on. What do you see?

Cellular Automata n n In Cellular. Automata. jar, look at rule 18. How many bits does it take to identify a particular rule? How many possible rules are there? Why is it called rule 30?

Rule 30 n n n Run rule 30 on random start. It looks very random. Where did that randomness come from? Run rule 30 from a single center point. It still looks very random. Where does the randomness come from? Read off the sequence down the middle column: 00100011101001101100010100010101001111001 n n Familiar? How much information is in this sequence?

Pseudo-random n n Rule 30 exhibits pseudo-randomness. Generated by an algorithm, but chaotic output. Fools us into thinking it's random. Computers use pseudorandom number generators to produce "random" behavior.

An Exercise n n n Start with a number from 1 to 10. Multiply by 7, and find remainder when divided by 11. That's the next number. Repeat.

An Exercise n (7 n) mod 11 Let's start with 4. What sequence do we get? n 4, 6, 9, 8, 1, 7, 5, 2, 3, 10, 4, . . . Does it look random?

Pseudo-Random n "(7 n) mod 11" exhibits pseudo-randomness. n A deterministic algorithm with chaotic output. n Fools us into thinking it's random. n Computers use pseudo-random number generators to produce "random" behavior.

An Exercise "(7 n) mod 11" generated: n 4, 6, 9, 8, 1, 7, 5, 2, 3, 10, 4, . . . What if I want to generate a longer pseudo-random sequence?

Pseudo-Random n (7 n) mod 101 Starting from 4: n 4, 28, 95, 59, 9, 63, 37, 57, 96, 66, 58, 2, 14, 98, 80, 55, 82, 69, 79, 48, 33, 29, 1, 7, 49, 40, 78, 41, 85, 90, 24, 67, 65, 51, 54, 75, 20, 39, 71, 93, 45, 12, 84, 83, 76, 27, 88, 10, 70, 86, 97, 73, 6, 42, 92, 38, 64, 44, 5, 35, 43, 99, 87, 3, 21, 46, 19, 32, 22, 53, 68, 72, 100, 94, 52, 61, 23, 60, 16, 11, 77, 34, 36, 50, 47, 26, 81, 62, 30, 8, 56, 89, 17, 18, 25, 74, 13, 91, 31, 15, 4, . . . n This gives us 100 numbers, in the range 1 to 100. n Suppose we want 100 numbers in the range 0 to 9. . .

Pseudo-Random Print ones digit only: n 4, 8, 5, 9, 9, 3, 7, 7, 2, 9, 9, 8, 3, 9, 1, 7, 5, 1, 4, 5, 0, 9, 1, 3, 0, 6, 7, 3, 6, 2, 2, 8, 1, 6, 9, 2, 2, 3, 8, 2, 7, 4, 6, 0, 7, 6, 1, 2, 3, 1, 1, 5, 4, . . . 6, 9, 5, 4, 0, 0, 6, 0, 2, 4, 4, 8, 8, 4, 5, 2, 6, 2, 1, 3, 5, 1, 9, 4, 5, 6, 3, 3, 7, 8, 0, 7, 9, 0, 8, 0, 4, 8, 7, 6, 5, 7, 0, 3, 1, 4,

Pseudo-Random n n "7 n mod 101" gives us the same numbers in the same order every time. If I want different behavior, I need to start at a different place in the sequence. n How do I choose which number to start from? n Pick a random one to start with? ? ?

Pseudo-Random n n I look at the current time to decide where to start. Why don't I just look at the time for every value?

Keno n n Anyone know how to play the casino game Keno? Numbers 1 to 80. You pick 20. The casino chooses 20. The prize depends on how many you get correct.

Keno n n n n In April 1994, college student Daniel Corriveau won $600, 000 CAD playing keno at the Casino de Montréal. He picked 19 of the 20 winning numbers. What are the odds of that? 1 in 3 thousand million. If you play once a minute, you would pick 19 -out-of 20 about every 5. 6 billion years. Daniel Corriveau picked 19 out of 20, 3 games in a row. How did he do that?

Keno n n n Keno is run on a computer. The numbers are generated by a pseudo-random number generator. When the machine is turned on, it uses a clock chip to determine where to start in the pseudo-random number sequence. 24 -hour casinos only turn on the Keno machine once ever. The clock chip for a Keno machine is sold separately. Therefore, some casinos stopped buying clock chips.

Keno n n n But this particular casino wasn't open 24 hours. So its Keno machine started once a day. Without the clock chip, it always started at the same point in its pseudo-random number sequence. So the sequence of winning numbers was the same every day. Daniel Corriveau got to keep his winnings.

True Randomness? n n If this is pseudorandomness, what processes result in true randomness? Is flipping a coin random or pseudorandom?

Food For Thought n Consider the complex arrangements of atoms that make up the people and things you see. Could some of that complexity have arisen from simple rules, too?

Food For Thought n n Is natural selection a set of simple rules that gets applied over and over again? How about the laws of physics?

Big Ideas n n more random = more information Complexity and pseudo-random behavior can arise from deterministic processes, where we repeatedly apply simple rules.