Motion Speed acceleration momentum Frames of Reference Object

Motion Speed, acceleration, momentum

Frames of Reference Object or point from which motion is determined n Most common is the earth n Motion is a change in position relative to a frame of reference n

What is motion? n If you are standing in one place, and your friend walks by you, are you moving relative to your friend? n Is your friend moving relative to you? n Is either of you moving relative to the earth?

n n You are moving relative to your friend, and your friend is moving relative to you! Answer: You (the Joker) are not moving relative to the earth, but your friend is. You are both moving relative to the sun! Who is moving relative to the computer screen?

What is motion? n If you and your friend are walking down the hall together at the same speed, in the same direction, are you moving relative to your friend? n Is your friend moving relative to you? n Are either of you moving relative to the earth?

Answer: n You are NOT moving relative to your friend, and your friend is NOT moving relative to you. You both are moving relative to the earth.

Speed = Distance ÷ Time D_ S T Example: A car travels 300 km in 6 hours. What is the speed of the car? n

Answer: n Speed = distance ÷ time n Speed = 300 km ÷ 6 hours n Speed = 50 km/hr

More practice n n 1. How far can a plane travel if it flies 800 km/hr for 9 hours? 2. How long does it take a ship to go 500 km if it travels at a speed of 50 km/hr?

Answer 1. D S T D 800 9 800 km ▪ 9 hrs = 7200 km hr

Answer 2. S D T 500 50 T 500 km ÷ 50 km = 10 hrs hr

Velocity n Speed n What in a given direction. is the velocity of a boat that travels from St. Peter to Mankato (10 miles) in 15 minutes?

Answer n Speed = distance ÷ time n Speed = 10 miles ÷ 15 minutes n Speed = 0. 67 mi/min n Velocity = 0. 67 mi/min South

Change your answer to mi/hr! n 0. 67 mi/min n 40 mi/hr x 60 min/hr =

Distance-time graphs n On your paper, graph the following: n D (m) 0 5 10 15 T (sec) 0 7 14 21

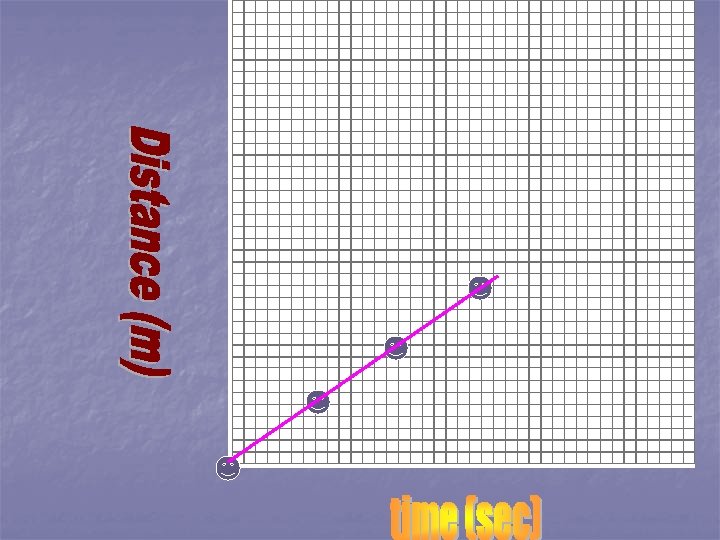
Was your graph a straight line? n. A distance-time graph which is a straight line indicates constant speed. n In constant speed, the object does not speed up or slow down. The acceleration is zero.

Graph the following on a distancetime graph: n D (m) 0 5 20 45 80 125 T (s) 0 1 2 3 4 5

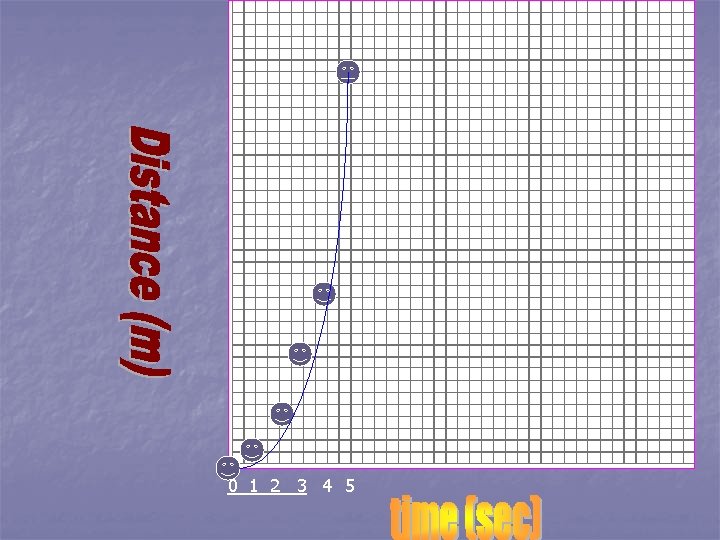
0 1 2 3 4 5

Was your graph a curve? n. A graph that curves on a distance -time graph shows that the object is accelerating

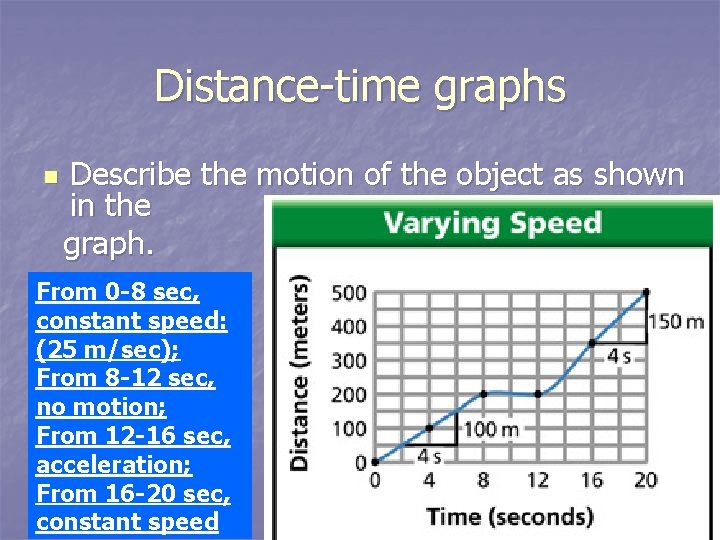
Distance-time graphs n Describe the motion of the object as shown in the graph. From 0 -8 sec, constant speed: (25 m/sec); From 8 -12 sec, no motion; From 12 -16 sec, acceleration; From 16 -20 sec, constant speed

Speed-time graphs n Using the distance-time graph from the last frame, draw a speed time graph. First fill in the table below: Average Speed (m/s) 25 ____ 0 ____ 37. 5 ____ Time (sec) 0 to 8 8 to 12 12 to 20

What does your graph look like? n Constant speed will be a horizontal line on a speed time graph. n If the speed decreases, the line will slant down. n If the speed increases, the line will slant up.

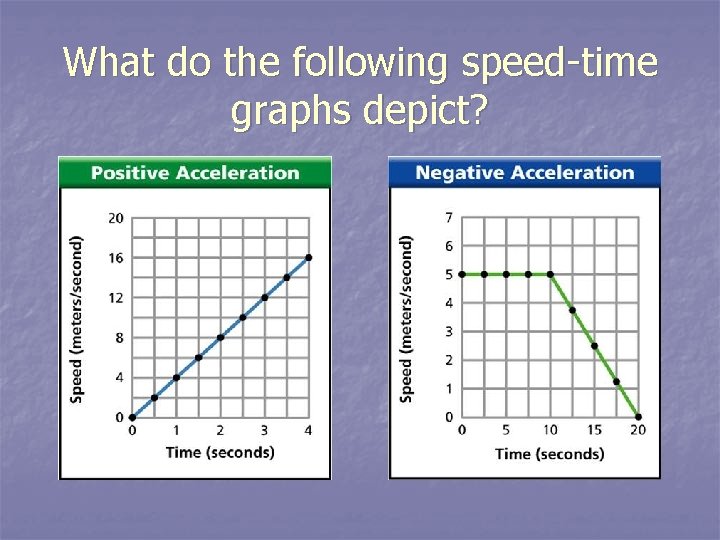
What do the following speed-time graphs depict?

Acceleration n Change n Can in velocity be change in speed or direction n Acceleration = Vi – Vf t

Acceleration problem n A roller coaster’s velocity at the top of a hill is 10 m/s. Two seconds later it reaches the bottom of the hill with a velocity of 26 m/s. What is the acceleration of the roller coaster?

Answer n Acceleration = ∆V/ ∆T n a = 26 m/s – 10 m/s 2 s a = 16 m/s 2 s a = 8 m/s/s or 8 m/s 2

More acceleration problems n n n 1. A car accelerates at a rate of 20 mi/hr/s. How long does it take to reach a speed of 80 mi/hr? 2. A car travels at 60 miles per hour around a curve. Is the car accelerating? 3. A car travels in a straight line at 60 mi/hr. Is the car accelerating?

Answers: 1. ∆V a t 80 mi/hr 20 mi/hr/s t 4 sec = t 2. yes! Because it’s changing direction! 3. no! It’s not changing speed or direction!

Deceleration n Negative acceleration n Example: A car slows from 60 mi/hr to 20 mi/hr in 4 seconds. What is its acceleration?

Answer: Acceleration = ∆V/ ∆T n Acceleration = Vf – Vi t n a = 20 mi/hr – 60 mi/hr 4 s a = -40 mi/hr 4 s a = -10 mi/hr/s n

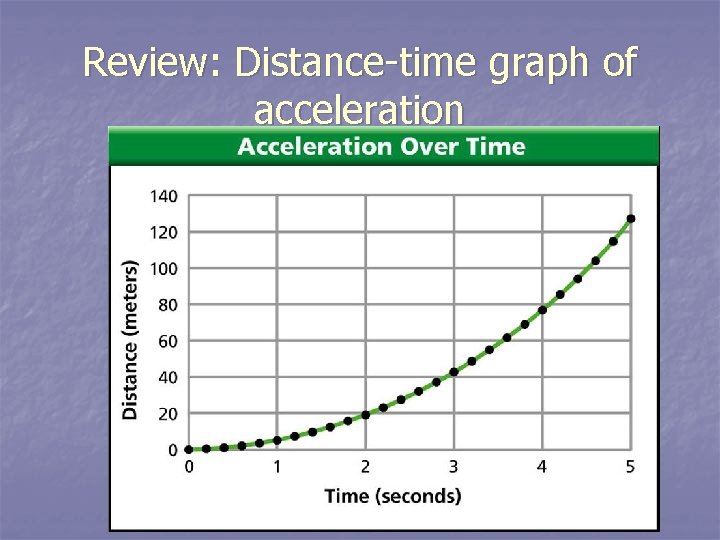
Review: Distance-time graph of acceleration

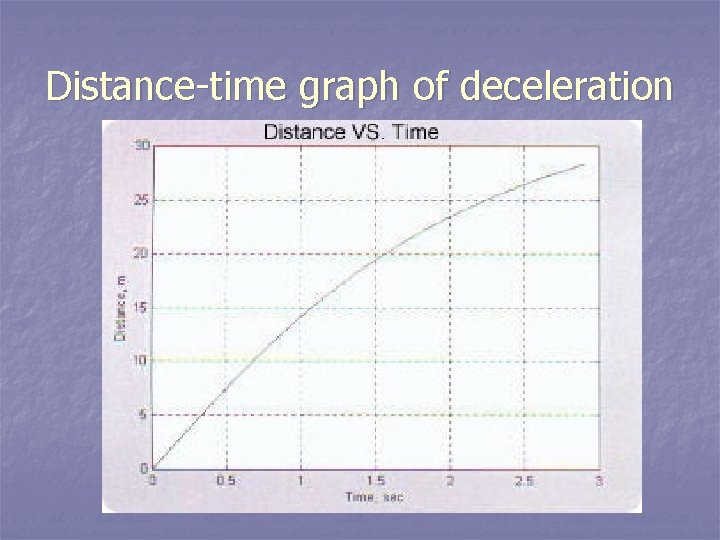
Distance-time graph of deceleration

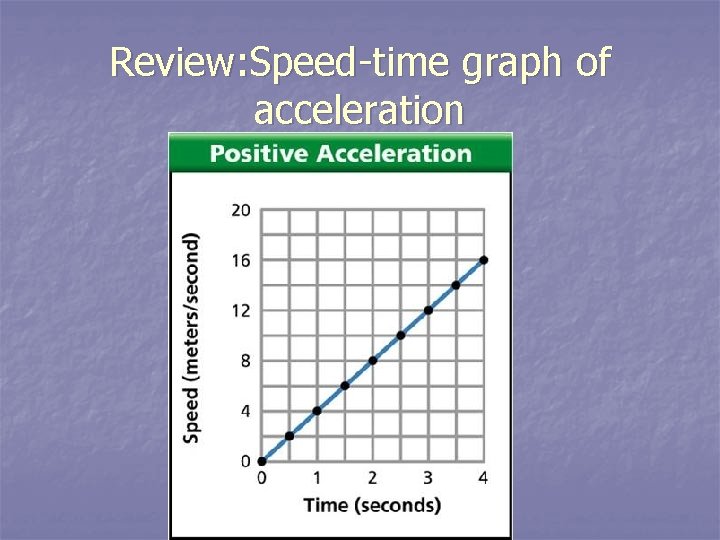
Review: Speed-time graph of acceleration

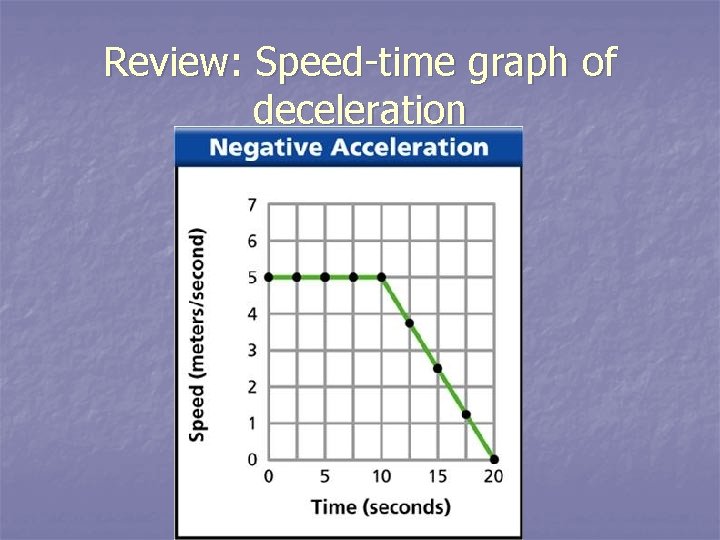
Review: Speed-time graph of deceleration

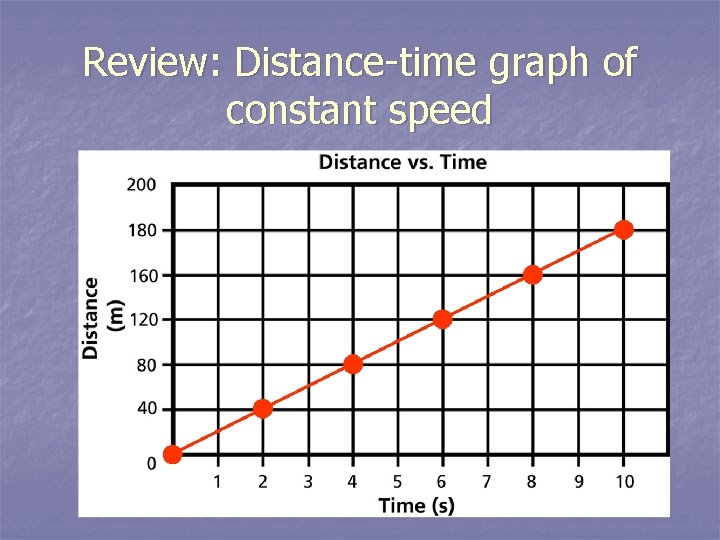
Review: Distance-time graph of constant speed

Momentum n Momentum = Mass x Velocity n Which has more momentum: a 300 lb football player moving at 5 m/s or a 200 lb quarterback moving at 10 m/s?

Answer: n Momentum of the 300 lb player is 300 lbs x 5 m/s = 1500 lb-m/s n Momentum of the quarterback is 200 lbs x 10 m/s = 2000 lb-m/s n The quarterback has a greater momentum!

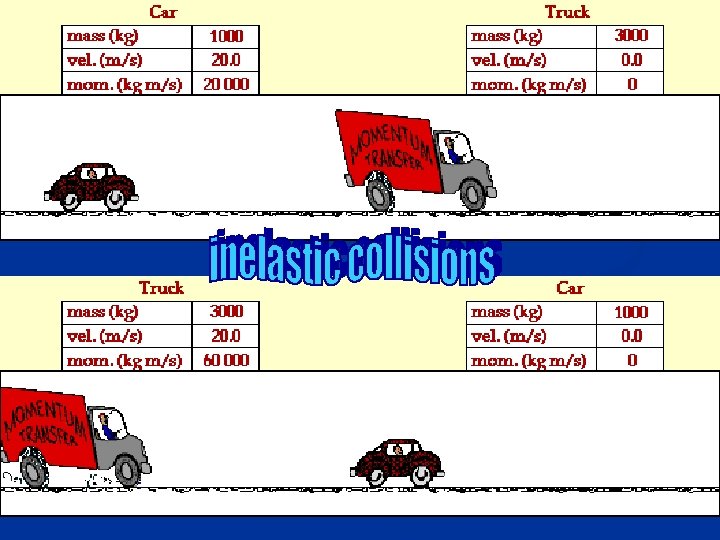
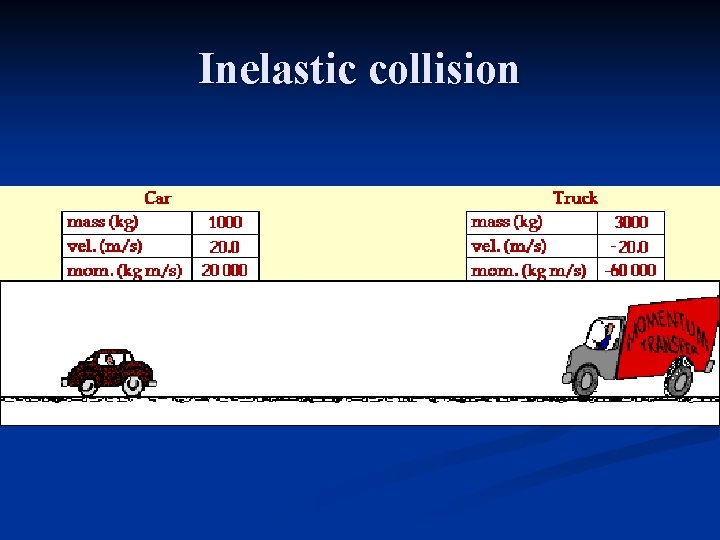
Inelastic collision

Elastic collision

Two dimensional collision

Momentum problems n 2 cars are heading east, car A is traveling 30 mi/hr, car B is traveling 60 mi/hr. Each car weighs 2000 lbs. n What is the momentum of car A? n What is the momentum of car B? n If car B crashes into car A, what is the total momentum?

Answers: P=mv n Car A’s momentum = 30 mi/hr x 2000 lbs PA = 60, 000 mi-lbs/hr east n Car B’s momentum = 60 mi/hr x 2000 lbs PB = 120, 000 mi-lbs/hr east n Total momentum = PA + PB = 60, 000 + 120, 000 = 180, 000 mi-lbs/hr east n

Another momentum problem! n Car X is traveling 30 mi/hr east, car Y is traveling 60 mi/hr west. Each car weighs 2000 lbs. n What is the momentum of car X? n What is the momentum of car Y? n If car X crashes into car Y, what is the total momentum?

Answers: P=mv n Car X’s momentum = 30 mi/hr x 2000 lbs PA = 60, 000 mi-lbs/hr east n Car Y’s momentum = 60 mi/hr x 2000 lbs PY = 120, 000 mi-lbs/hr west n Total momentum = PY - PX = 120, 000 - 60, 000 = 60, 000 mi-lbs/hr west n

Which has more momentum?