Motion Segmentation from Clustering of Sparse Point Features

Motion Segmentation from Clustering of Sparse Point Features Using Spatially Constrained Mixture Models Shrinivas Pundlik Committee members Dr. Stan Birchfield (chair) Dr. Adam Hoover Dr. Ian Walker Dr. Damon Woodard

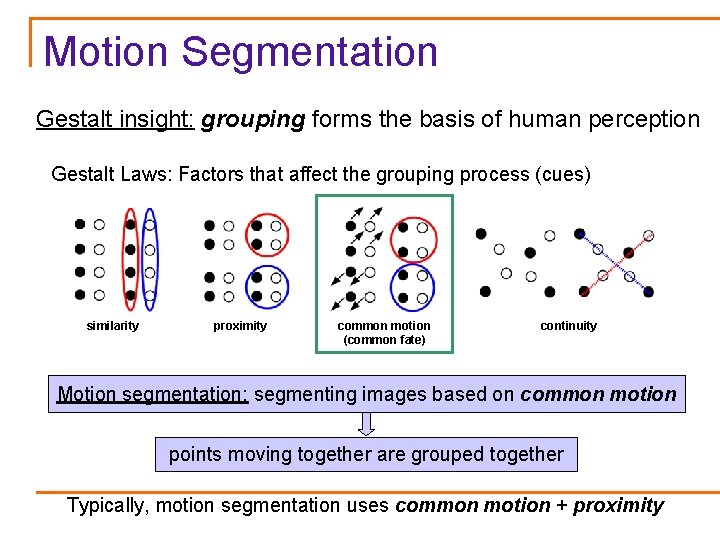
Motion Segmentation Gestalt insight: grouping forms the basis of human perception Gestalt Laws: Factors that affect the grouping process (cues) similarity proximity common motion (common fate) continuity Motion segmentation: segmenting images based on common motion points moving together are grouped together Typically, motion segmentation uses common motion + proximity

Applications of Motion Segmentation n object detection q n tracking q n n n pedestrian detection vehicle tracking robotics surveillance image and video compression scene reconstruction video manipulation / editing q q q video matting video annotation motion magnification Pedestrian detection Viola et al. , 2003 Vehicle tracking Kanhere et al. , 2005 Video editing Criminisi et al. , 2006

Previous Work Approach Motion Layer Estimation Algorithm Expectation Maximization Wang and Adelson 1994 Jojic and Frey 2001 Ayer and Sawhney 1995 Jojic and Frey 2001 Willis et al. 2003 Smith et al. 2004 Kokkinos and Maragos 2004 Xiao and Shah 2005 Multi Body Factorization Costeria and Kanade 1995 Ke and Kanade 2002 Vidal and Sastry 2003 Yan and Pollefeys 2006 Gruber and Weiss 2006 Object Level Grouping Sivic et al. 2004 Kanhere et al. 2005 Miscellaneous Black and Fleet 1998 Birchfield 1999 Levine and Weiss 2006 Graph Cuts Willis et al. 2003 Xiao and Shah 2005 Criminisi et al. 2006 Normalized Cuts Shi and Malik 1998 Belief Propagation Kumar et al. 2005 Variational Methods Cremers and Soatto 2005 Brox et al. 2005 Nature of Data Sparse Features Sivic et al. 2004 Kanhere et al. 2005 Rothganger et al. 2004 Dense Motion Cremers and Soatto 2005 Brox et al. 2005 Motion + Image Cues Xiao and Shah 2005 Kumar et al. 2005 Criminisi et al. 2006

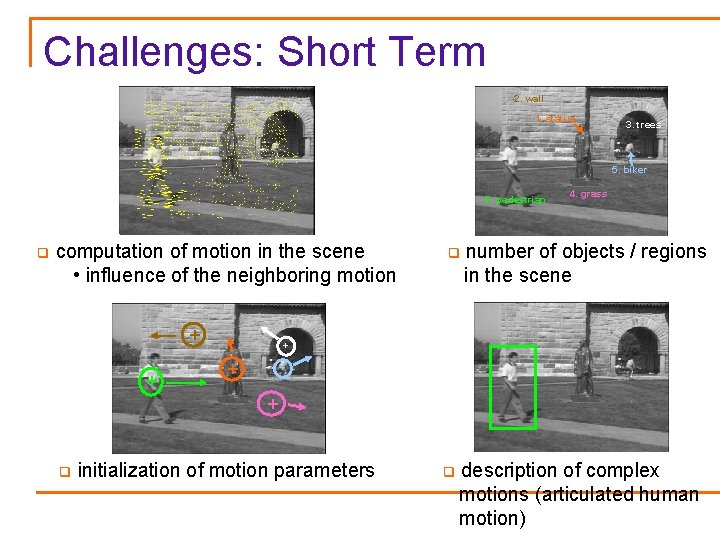
Challenges: Short Term 2. wall 1. statue 3. trees 5. biker 6. pedestrian q computation of motion in the scene • influence of the neighboring motion + + q 4. grass number of objects / regions in the scene + + q initialization of motion parameters q description of complex motions (articulated human motion)

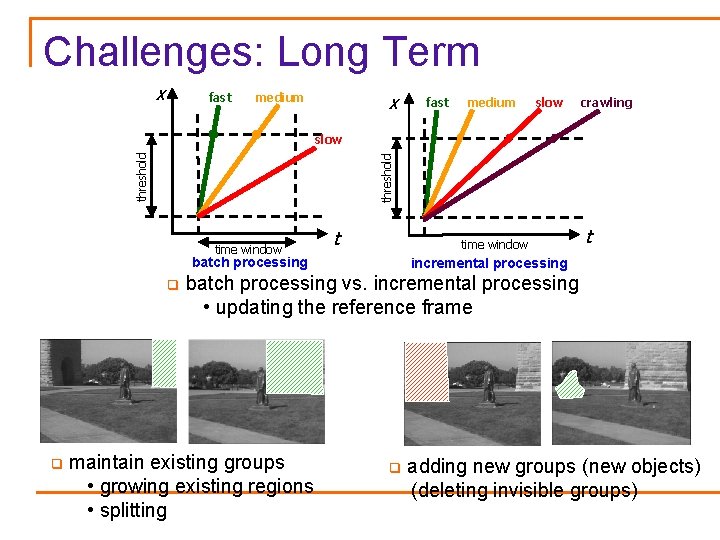
Challenges: Long Term x fast x medium fast medium slow crawling threshold slow time window t time window batch processing q q t incremental processing batch processing vs. incremental processing • updating the reference frame maintain existing groups • growing existing regions • splitting q adding new groups (new objects) (deleting invisible groups)

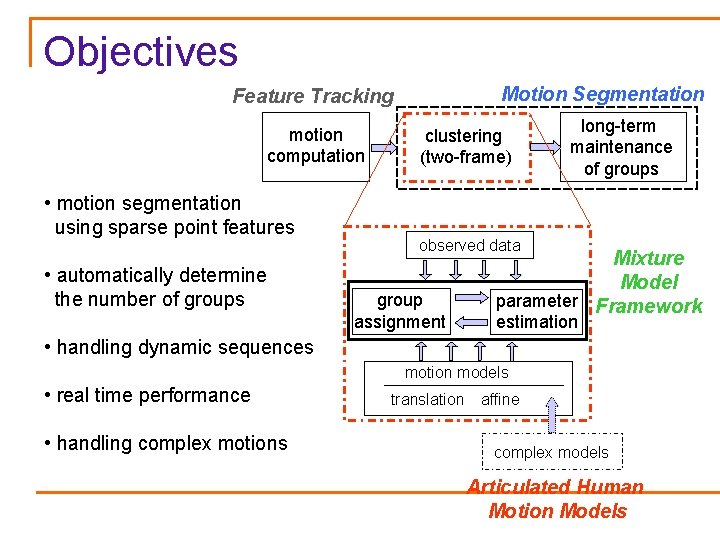
Objectives Motion Segmentation Feature Tracking motion computation • motion segmentation using sparse point features • automatically determine the number of groups clustering (two-frame) long-term maintenance of groups observed data group assignment Mixture Model parameter Framework estimation • handling dynamic sequences motion models • real time performance • handling complex motions translation affine complex models Articulated Human Motion Models

Overview of the Topics n Feature Tracking: Tracking sparse point features for computation of image motion and its extension to joint feature tracking. q n S. T. Birchfield and S. J. Pundlik, “Joint Tracking of Features and Edges”, CVPR, 2008. Motion Segmentation: Clustering point features in videos based on their motion and spatial connectivity. q q S. J. Pundlik and S. T. Birchfield, “Motion Segmentation at Any Speed”, BMVC 2006. S. J. Pundlik and S. T. Birchfield, “Real Time Motion Segmentation of Sparse Feature Points at Any Speed”, IEEE Trans. on Systems, Man, and Cybernetics, 2008. n Articulated Human Motion Models: Learning n Iris Segmentation: Texture and intensity based human walking motion from various pose and view angles for segmentation and pose estimation (a special handling of a complex motion model) segmentation of non-ideal iris images. q S. J. Pundlik, D. L. Woodard and S. T. Birchfield, “Non Ideal Iris Segmentation Using Graph Cuts”, CVPR Workshop on Biometrics, 2008.

Point Features input gradients point features capturing the information content Popular features: Harris corner feature [Harris & Stephens 1987, Schmid et al. 2000] q Shi-Tomasi feature [Shi & Tomasi 1994] q Forstner corner feature [Forstner 1994] q Scale invariant feature transform (SIFT) [Lowe 2000] q Gradient Location and Orientation Histogram (GLOH) [Mikolajczyk and Schmid 2005] q Features from accelerated segment test (FAST) [Rosten and Drummond 2005] q Speeded up robust features (SURF) [Bay et al. 2006] q DAISY [Tola et al. 2008] q

Utility of Point Features Advantages: q highly repeatable and extensible (work for a variety of images) q efficient to compute (real time implementations available) q local methods for processing (tracking through multiple frames) tracking multiple point features = sparse optical flow sparse point feature tracks yield the image motion

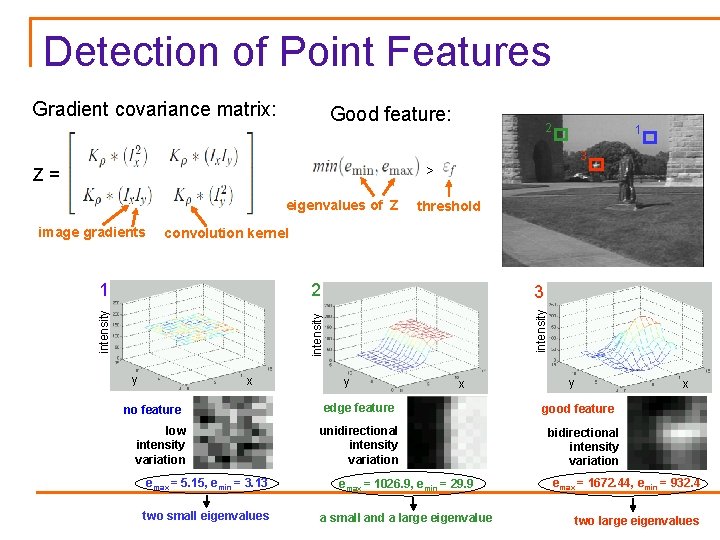
Tracking Point Features : Lucas. Assume constant brightness: Kanade image pixel displacement image spatial derivatives (optic flow constraint equation) image temporal derivative Estimate the pixel displacement u = ( u, v )T by minimizing: convolution kernel Differentiating with respect to u and v, setting the derivatives to zero leads to a linear system: Iterate using Newton-Raphson method Gradient covariance matrix

Detection of Point Features Gradient covariance matrix: Good feature: 2 1 3 > Z= eigenvalues of Z image gradients threshold convolution kernel 2 intensity 3 intensity 1 y x no feature low intensity variation y x edge feature unidirectional intensity variation emax = 5. 15, emin = 3. 13 emax = 1026. 9, emin = 29. 9 two small eigenvalues a small and a large eigenvalue y x good feature bidirectional intensity variation emax = 1672. 44, emin = 932. 4 two large eigenvalues

Dense Optical Flow: Horn-Schunck: find global displacement functions u(x, y) and v(x, y) by minimizing: regularization parameter data term (optical flow constraint) Solve using Euler-Lagrange: Approximation smoothness term Laplacian leads to a sparse system: a constant average displacement in the neighborhood

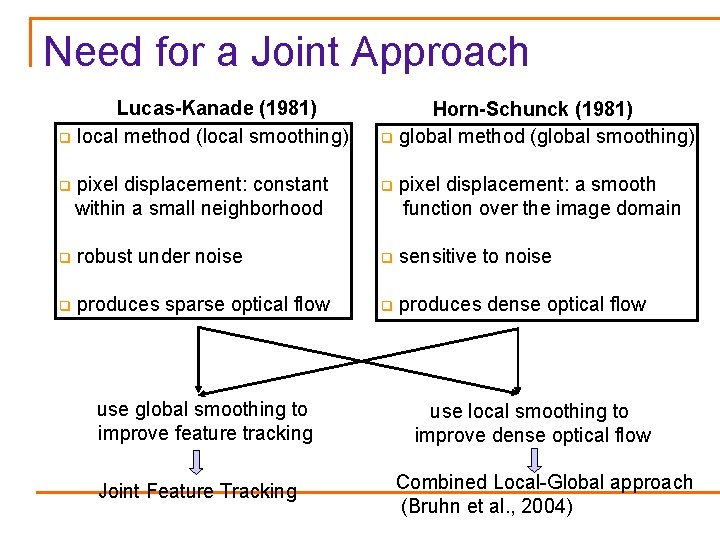
Need for a Joint Approach Lucas-Kanade (1981) q local method (local smoothing) Horn-Schunck (1981) q global method (global smoothing) q pixel displacement: constant within a small neighborhood q pixel displacement: a smooth function over the image domain q robust under noise q sensitive to noise q produces sparse optical flow q produces dense optical flow use global smoothing to improve feature tracking Joint Feature Tracking use local smoothing to improve dense optical flow Combined Local-Global approach (Bruhn et al. , 2004)

Joint Lucas-Kanade (JLK) Joint Lucas-Kanade energy functional: number of feature points expected values data term (optical flow constraint) smoothness term (regularization) Differentiating EJLK w. r. t. (u, v) gives a 2 N x 2 N system whose (2 i-1) and (2 i)th rows are given by: Sparse system is solved using Jacobi iterations

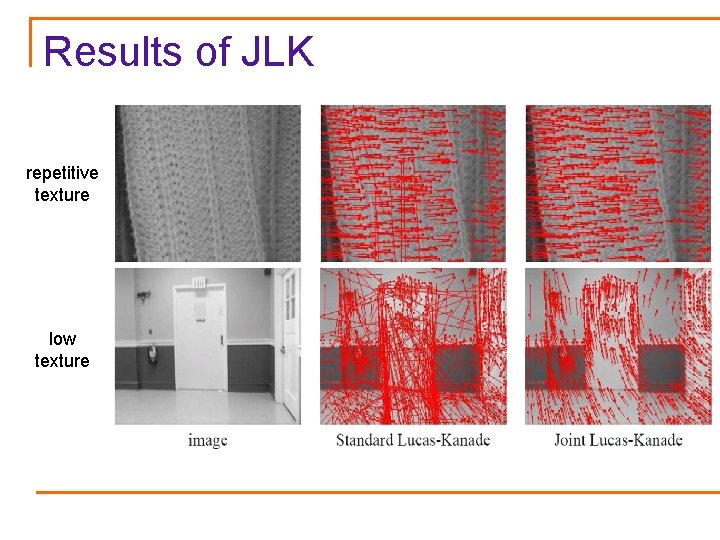
Results of JLK repetitive texture low texture

Overview of the Topics n Feature Tracking: Tracking sparse point features for computation of image motion and its extension to joint feature tracking. q n S. T. Birchfield and S. J. Pundlik, “Joint Tracking of Features and Edges”, CVPR, 2008. Motion Segmentation: Clustering point features in videos based on their motion and spatial connectivity. q q S. J. Pundlik and S. T. Birchfield, “Motion Segmentation at Any Speed”, BMVC 2006. S. J. Pundlik and S. T. Birchfield, “Real Time Motion Segmentation of Sparse Feature Points at Any Speed”, IEEE Trans. on Systems, Man, and Cybernetics, 2008. n Articulated Human Motion Models: Learning n Iris Segmentation: Texture and intensity based human walking motion from various pose and view angles for segmentation and pose estimation (a special handling of a complex motion model) segmentation of non-ideal iris images. q S. J. Pundlik, D. L. Woodard and S. T. Birchfield, “Non Ideal Iris Segmentation Using Graph Cuts”, CVPR Workshop on Biometrics, 2008.

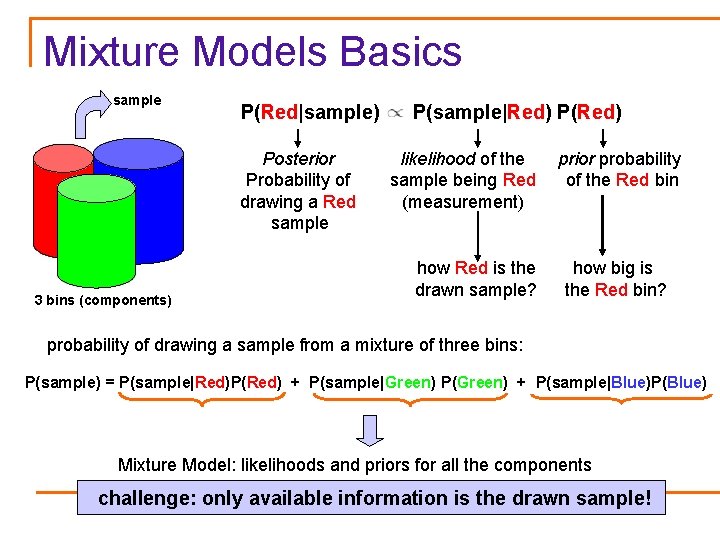
Mixture Models Basics sample P(Red|sample) Posterior Probability of drawing a Red sample 3 bins (components) P(sample|Red) P(Red) likelihood of the sample being Red (measurement) how Red is the drawn sample? prior probability of the Red bin how big is the Red bin? probability of drawing a sample from a mixture of three bins: P(sample) = P(sample|Red)P(Red) + P(sample|Green) P(Green) + P(sample|Blue)P(Blue) Mixture Model: likelihoods and priors for all the components challenge: only available information is the drawn sample!

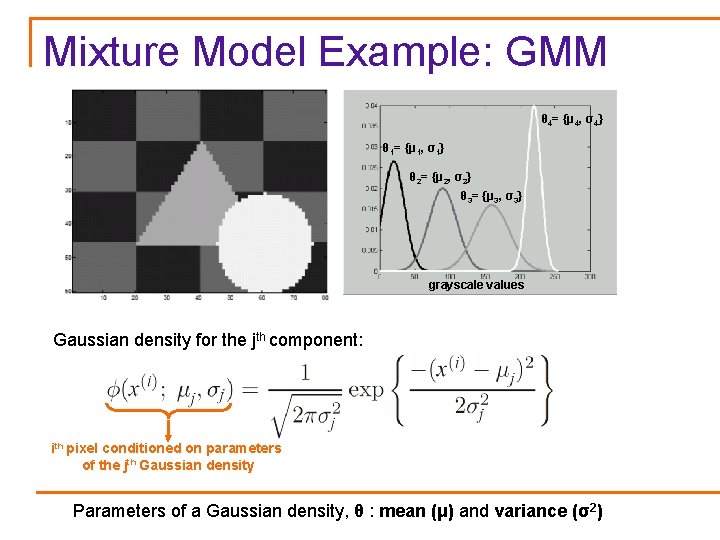
Mixture Model Example: GMM θ 4= {μ 4, σ4} θ 1= {μ 1, σ1} θ 2= {μ 2, σ2} θ 3= {μ 3, σ3} grayscale values Gaussian density for the jth component: ith pixel conditioned on parameters of the jth Gaussian density Parameters of a Gaussian density, θ : mean (μ) and variance (σ2)

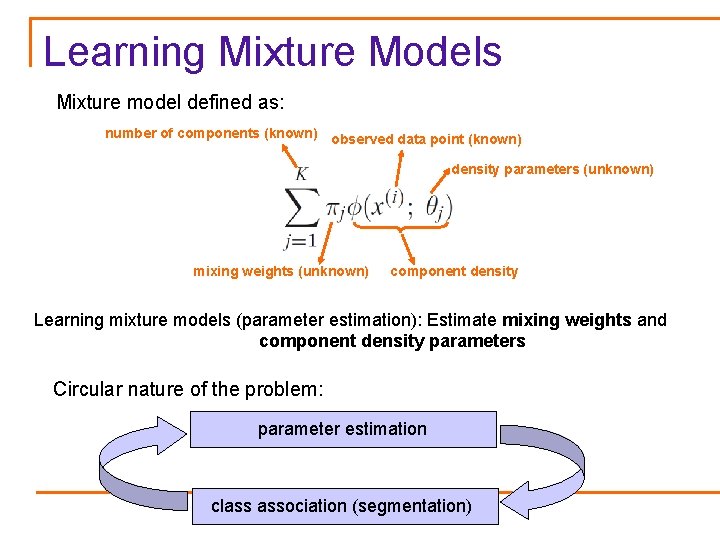
Learning Mixture Models Mixture model defined as: number of components (known) observed data point (known) density parameters (unknown) mixing weights (unknown) component density Learning mixture models (parameter estimation): Estimate mixing weights and component density parameters Circular nature of the problem: parameter estimation class association (segmentation)

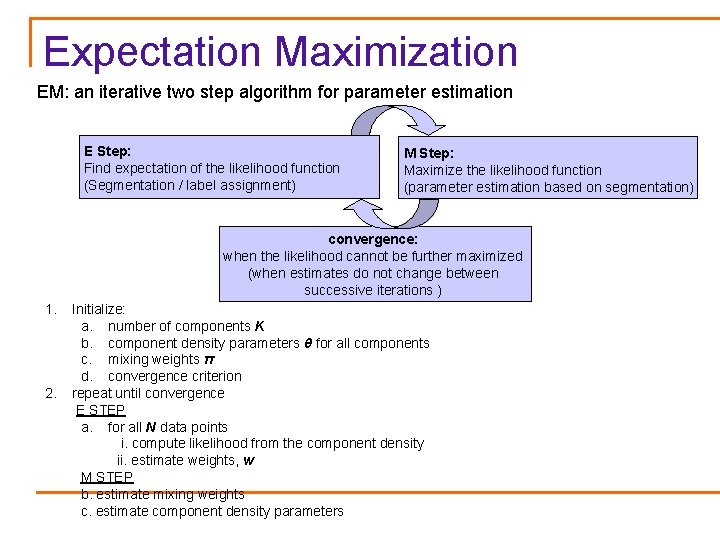
Expectation Maximization EM: an iterative two step algorithm for parameter estimation E Step: Find expectation of the likelihood function (Segmentation / label assignment) M Step: Maximize the likelihood function (parameter estimation based on segmentation) convergence: when the likelihood cannot be further maximized (when estimates do not change between successive iterations ) 1. 2. Initialize: a. number of components K b. component density parameters θ for all components c. mixing weights π d. convergence criterion repeat until convergence E STEP a. for all N data points i. compute likelihood from the component density ii. estimate weights, w M STEP b. estimate mixing weights c. estimate component density parameters

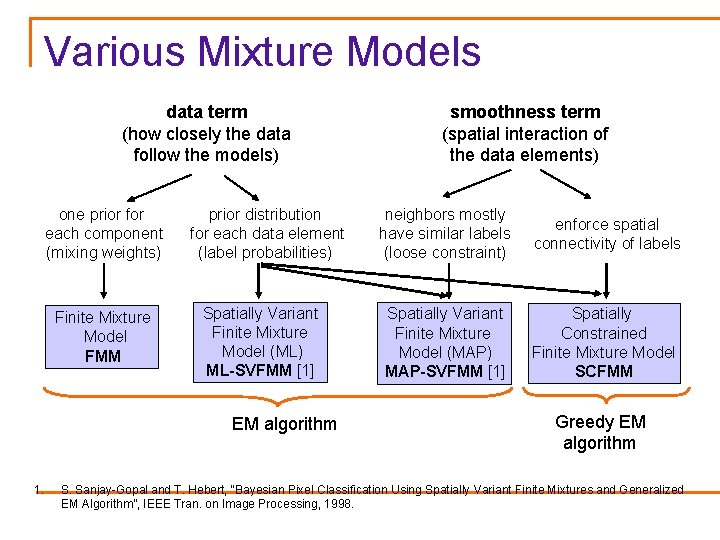
Various Mixture Models data term (how closely the data follow the models) one prior for each component (mixing weights) Finite Mixture Model FMM prior distribution for each data element (label probabilities) Spatially Variant Finite Mixture Model (ML) ML-SVFMM [1] EM algorithm 1. smoothness term (spatial interaction of the data elements) neighbors mostly have similar labels (loose constraint) enforce spatial connectivity of labels Spatially Variant Finite Mixture Model (MAP) MAP-SVFMM [1] Spatially Constrained Finite Mixture Model SCFMM Greedy EM algorithm S. Sanjay-Gopal and T. Hebert, “Bayesian Pixel Classification Using Spatially Variant Finite Mixtures and Generalized EM Algorithm”, IEEE Tran. on Image Processing, 1998.

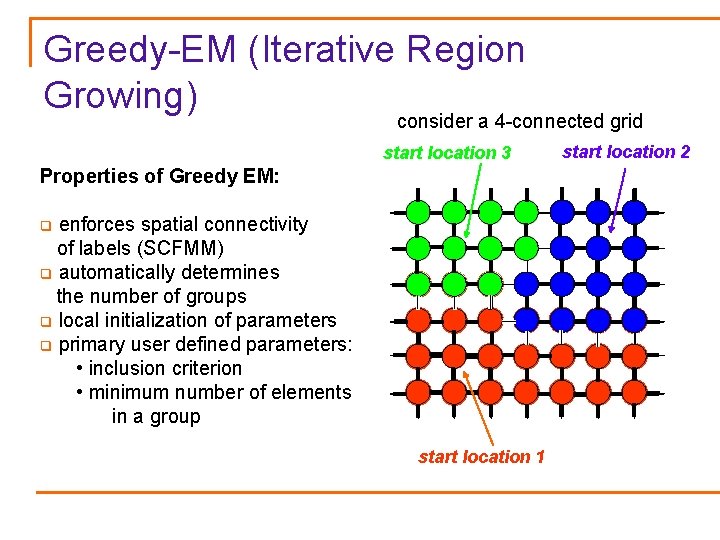
Greedy-EM (Iterative Region Growing) consider a 4 -connected grid start location 3 Properties of Greedy EM: enforces spatial connectivity of labels (SCFMM) q automatically determines the number of groups q local initialization of parameters q primary user defined parameters: • inclusion criterion • minimum number of elements in a group q start location 1 start location 2

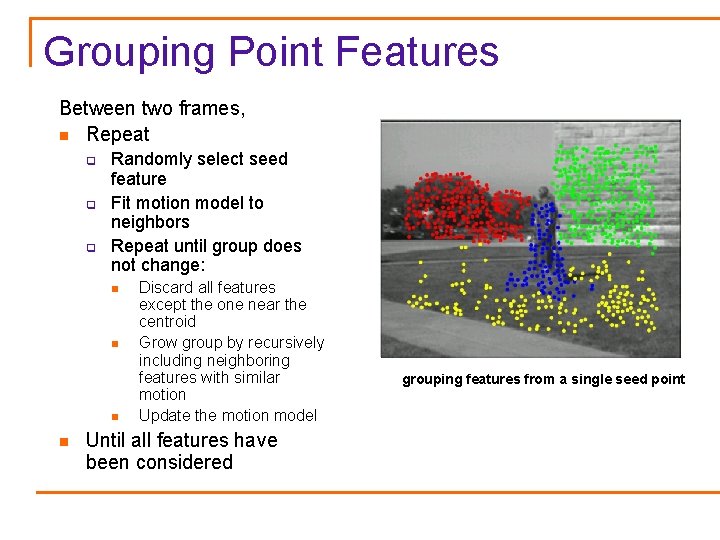
Grouping Point Features Between two frames, n Repeat q q q Randomly select seed feature Fit motion model to neighbors Repeat until group does not change: n n Discard all features except the one near the centroid Grow group by recursively including neighboring features with similar motion Update the motion model Until all features have been considered centroid centroid original seed grouping features from a single seed point

Grouping Consistent Features n n n input: point features tracked between two frames output: groups of point features for N seed points q q seed 2 seed 1 seed 3 group point features gather sets of features always grouped together consistent feature group

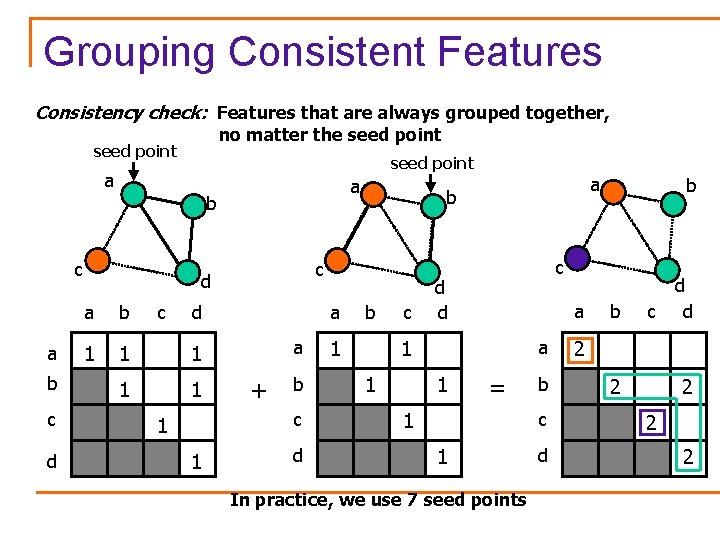
Grouping Consistent Features Consistency check: Features that are always grouped together, no matter the seed point a a b c d a b c 1 1 1 d a a + b c 1 1 b c d d a b 1 c c d d a 1 1 a 1 b = 1 b c 1 In practice, we use 7 seed points d b d c d 2 2 2

Consistent Features: Multiple Groups Feature groups obtained for various iterations consistent feature groups

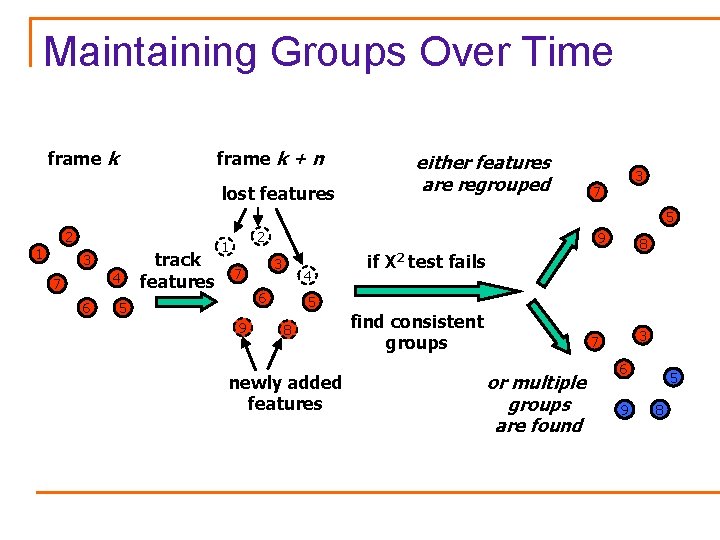
Maintaining Groups Over Time frame k + n either features are regrouped lost features 3 7 5 2 1 3 4 7 6 track features 2 1 9 3 7 4 6 5 96 5 86 newly added features if Х 2 8 test fails find consistent groups 3 7 or multiple groups are found 6 9 5 8

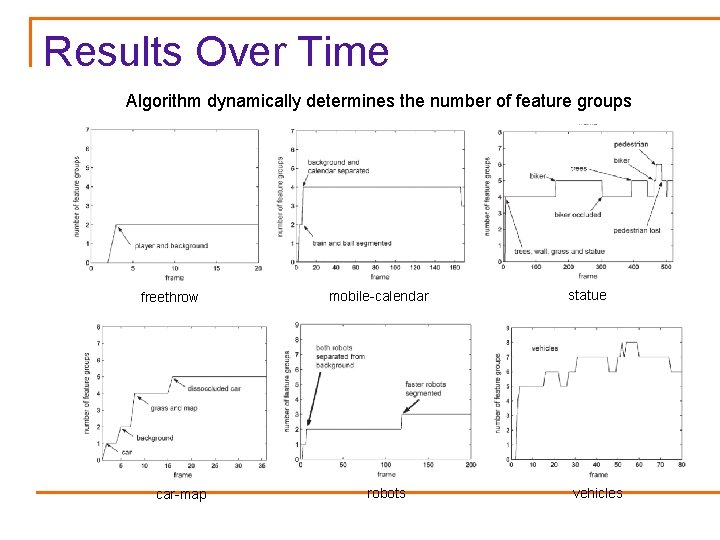
Experimental Results freethrow mobile-calendar statue robots car-map

Videos mobile-calendar sequence statue sequence

Results Over Time Algorithm dynamically determines the number of feature groups freethrow car-map mobile-calendar robots statue vehicles

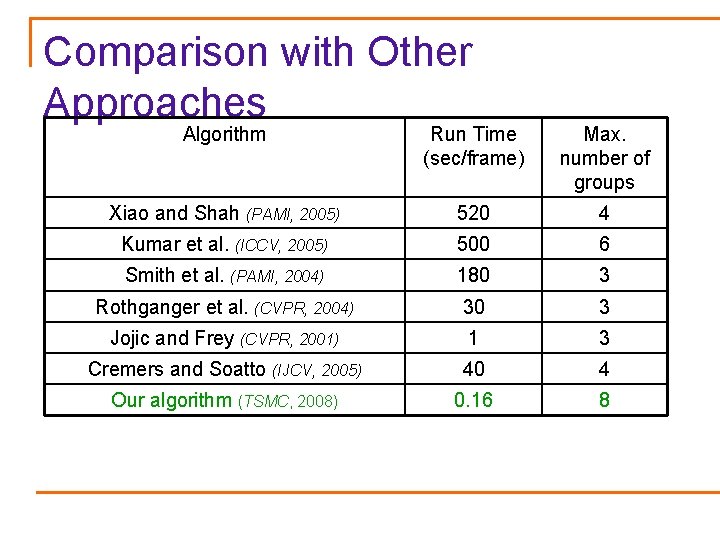
Comparison with Other Approaches Algorithm Run Time (sec/frame) Max. number of groups Xiao and Shah (PAMI, 2005) 520 4 Kumar et al. (ICCV, 2005) 500 6 Smith et al. (PAMI, 2004) 180 3 Rothganger et al. (CVPR, 2004) 30 3 Jojic and Frey (CVPR, 2001) 1 3 Cremers and Soatto (IJCV, 2005) 40 4 Our algorithm (TSMC, 2008) 0. 16 8

Effect of Joint Feature Tracking input standard Lucas-Kanade Joint Lucas-Kanade

Overview of the Topics n Feature Tracking: Tracking sparse point features for computation of image motion and its extension to joint feature tracking. q n S. T. Birchfield and S. J. Pundlik, “Joint Tracking of Features and Edges”, CVPR, 2008. Motion Segmentation: Clustering point features in videos based on their motion and spatial connectivity. q q S. J. Pundlik and S. T. Birchfield, “Motion Segmentation at Any Speed”, BMVC 2006. S. J. Pundlik and S. T. Birchfield, “Real Time Motion Segmentation of Sparse Feature Points at Any Speed”, IEEE Trans. on Systems, Man, and Cybernetics, 2008. n Articulated Human Motion Models: Learning n Iris Segmentation: Texture and intensity based human walking motion from various pose and view angles for segmentation and pose estimation (a special handling of a complex motion model) segmentation of non-ideal iris images. q S. J. Pundlik, D. L. Woodard and S. T. Birchfield, “Non Ideal Iris Segmentation Using Graph Cuts”, CVPR Workshop on Biometrics, 2008.

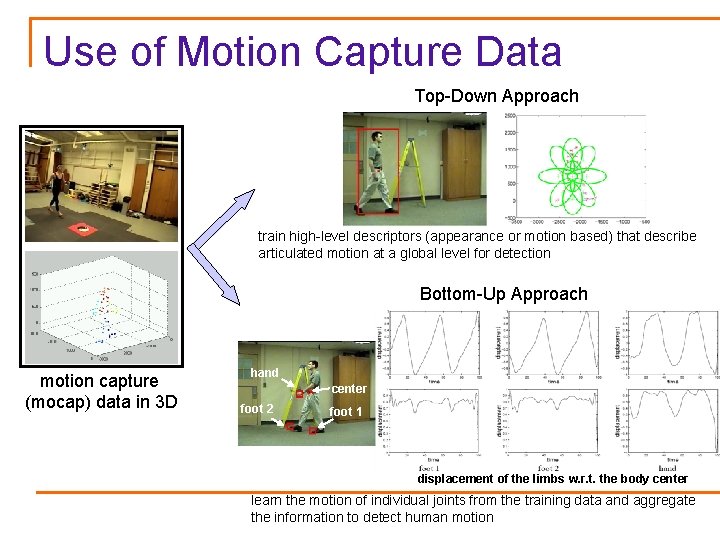
Articulated Motion Models Purpose of human motion analysis: q pedestrian detection/surveillance q action recognition q pose estimation Traditional approaches use: q appearance q frame differencing Theme: Sparse Motion alone captures a wealth of information Objectives: q learn articulated human motion models q motion only, no appearance q viewpoint and scale invariant detection q varying lighting conditions (day and night time sequences) q detection in presence of camera and background motion q pose estimation

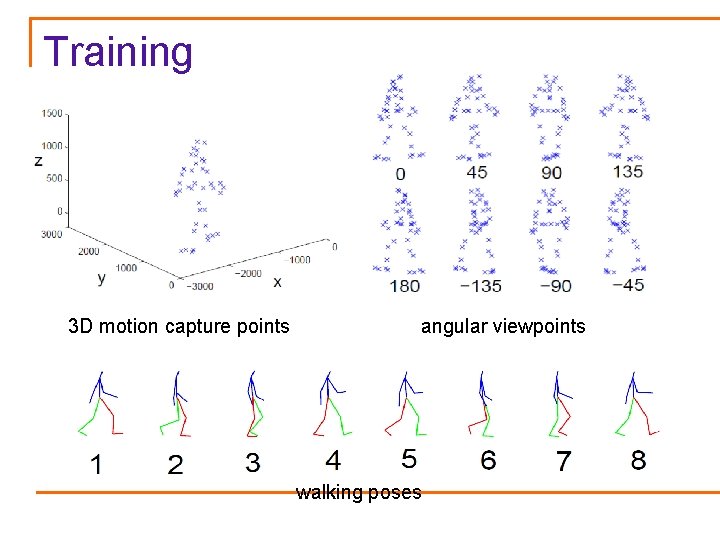
Use of Motion Capture Data Top-Down Approach train high-level descriptors (appearance or motion based) that describe articulated motion at a global level for detection Bottom-Up Approach motion capture (mocap) data in 3 D hand center foot 2 foot 1 displacement of the limbs w. r. t. the body center learn the motion of individual joints from the training data and aggregate the information to detect human motion

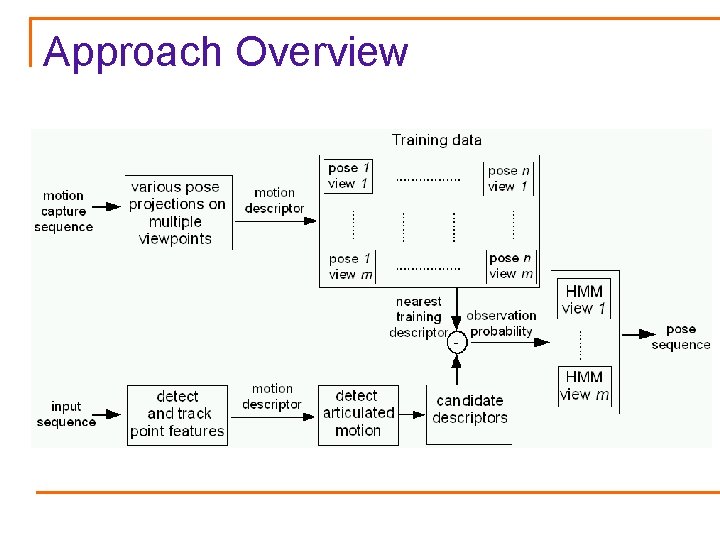
Approach Overview

Training 3 D motion capture points angular viewpoints walking poses

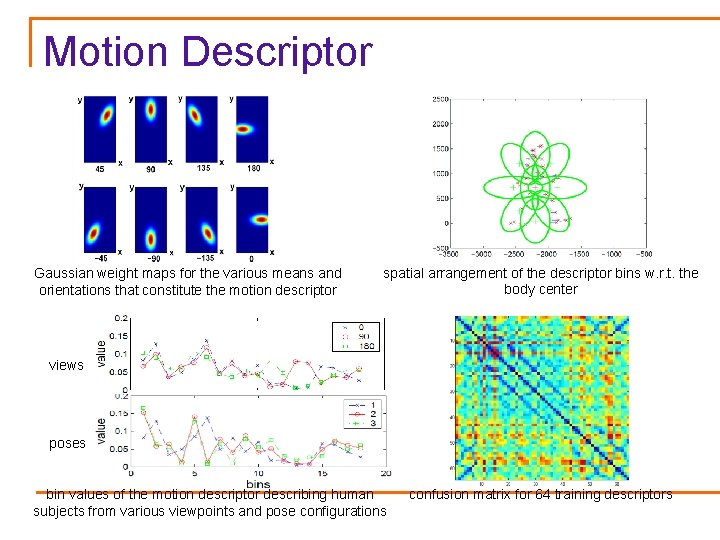
Motion Descriptor Gaussian weight maps for the various means and orientations that constitute the motion descriptor spatial arrangement of the descriptor bins w. r. t. the body center views poses bin values of the motion descriptor describing human subjects from various viewpoints and pose configurations confusion matrix for 64 training descriptors

Segmentation Results right profile left profile angular front View-invariant segmentation of articulated motion using a motion descriptor Segmentation of articulated motion in a challenging sequence involving camera and background motion

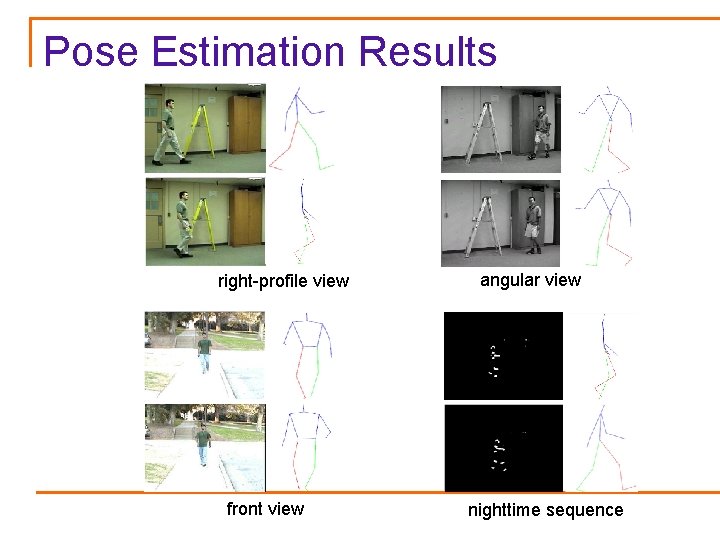
Pose Estimation Results right-profile view front view angular view nighttime sequence

Videos of Detection and Pose Estimation

Overview of the Topics n Feature Tracking: Tracking sparse point features for computation of image motion and its extension to joint feature tracking. q n S. T. Birchfield and S. J. Pundlik, “Joint Tracking of Features and Edges”, CVPR, 2008. Motion Segmentation: Clustering point features in videos based on their motion and spatial connectivity. q q S. J. Pundlik and S. T. Birchfield, “Motion Segmentation at Any Speed”, BMVC 2006. S. J. Pundlik and S. T. Birchfield, “Real Time Motion Segmentation of Sparse Feature Points at Any Speed”, IEEE Trans. on Systems, Man, and Cybernetics, 2008. n Articulated Human Motion Models: Learning n Iris Segmentation: Texture and intensity based human walking motion from various pose and view angles for segmentation and pose estimation (a special handling of a complex motion model) segmentation of non-ideal iris images. q S. J. Pundlik, D. L. Woodard and S. T. Birchfield, “Non Ideal Iris Segmentation Using Graph Cuts”, CVPR Workshop on Biometrics, 2008.

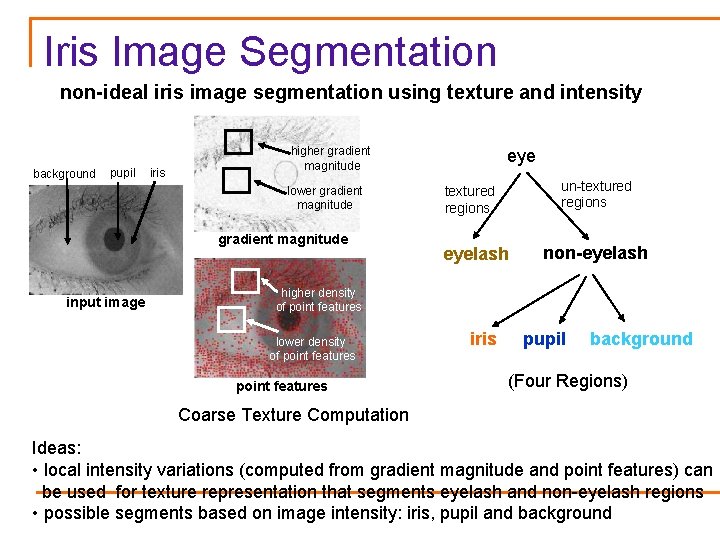
Iris Image Segmentation non-ideal iris image segmentation using texture and intensity background pupil iris higher gradient magnitude lower gradient magnitude input image eye un-textured regions eyelash non-eyelash higher density of point features lower density of point features iris pupil background (Four Regions) Coarse Texture Computation Ideas: • local intensity variations (computed from gradient magnitude and point features) can be used for texture representation that segments eyelash and non-eyelash regions • possible segments based on image intensity: iris, pupil and background

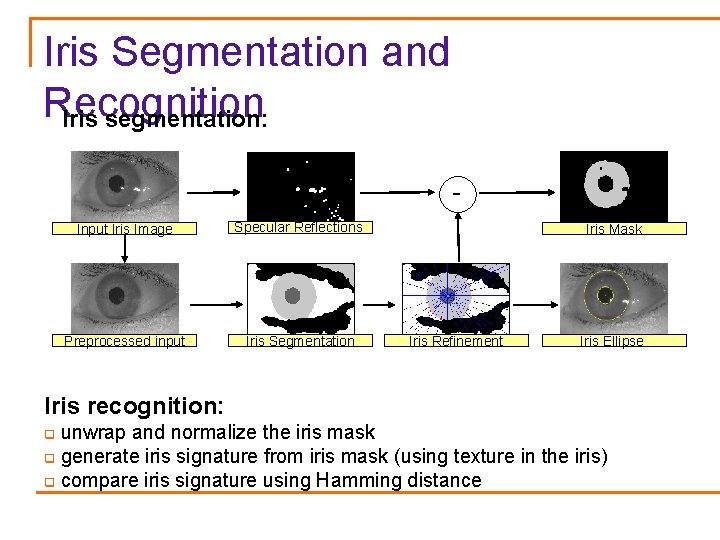
Iris Segmentation and Recognition Iris segmentation: Input Iris Image Specular Reflections Preprocessed input Iris Segmentation Iris Mask Iris Refinement Iris Ellipse Iris recognition: unwrap and normalize the iris mask q generate iris signature from iris mask (using texture in the iris) q compare iris signature using Hamming distance q

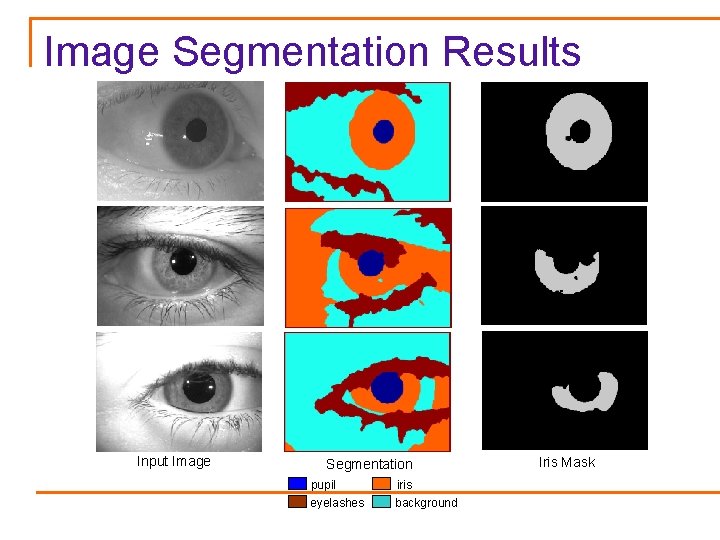
Image Segmentation Results Input Image Segmentation pupil iris eyelashes background Iris Mask

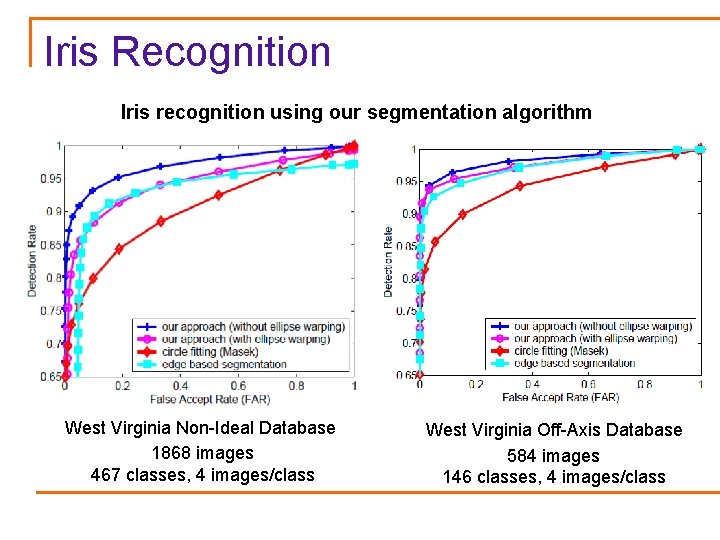
Iris Recognition Iris recognition using our segmentation algorithm West Virginia Non-Ideal Database 1868 images 467 classes, 4 images/class West Virginia Off-Axis Database 584 images 146 classes, 4 images/class

Conclusions and Future Work n Motion segmentation based on sparse feature clustering q spatially constrained mixture model and greedy EM algorithm q automatically determines number of groups q real-time performance q ability to handle long, dynamic sequences and arbitrary number of feature groups n Joint feature tracking q incorporation of neighboring feature motion q improved performance in areas of low-texture or repetitive texture n Detection of articulated motion q motion based approach for learning high-level human motion models q segment and track human motion in varying pose, scale, and lighting conditions q view invariant pose estimation n Iris segmentation q graph cuts based dense segmentation using texture and intensity q combines appearance and eye geometry q handles non-ideal iris image with occlusion, illumination changes, and eye rotation n Future Work q integration of motion segmentation, joint feature tracking, and articulated motion segmentation q dense segmentation from the sparse feature groups q handling non-rigid motions, non-textured regions, and occlusions q combining sparse feature groups, discontinuities, and image contours for a novel representation of video

Questions?