Motion Physics Unit 2 Describing Movement Definitions A

Motion Physics: Unit 2

Describing Movement Definitions A vecto quantity specifies direction as well as magnitude What is a rscalar ? (size). A quantity specifies the magnitude but not the And what is a R direction. A L ? A C S R O T C Distance is a measure of length of a path taken by an object. VE Displacement is a measure of the change in position of an object.

Describing Movement Applying these concepts to problems eg 1. Rowan walks from his locker up to his Maths classroom located 50 metres away in a northerly direction, but realises halfway there that he has forgotten his calculator. He walks back to his locker, collects the calculator and goes to class. a) What is the distance travelled by Rowan after this journey? Total Distance = Halfway to maths + Back to Locker + All the way to maths = 25 m + 50 m = 100 m b) What is the displacement of Rowan after this journey? Distance is a measure of length of a path taken by an objec Displacement is a measure of the change in position of an ob

Describing Movement Definitions R A L A SC Speed is ‘how fast an object moves’, or the rate at which an object covers a distance. R O T C E V Velocity is a measure of ‘the rate at which an object changes its position’. Are speed and velocity scalars or vectors? Understanding Velocity…… A person moves rapidly - one step forward and one step back - always returning to the original starting position. Because the person always returns to the original position, the motion would never result in a change in position. This would result in a zero velocity, since velocity is defined as the rate at which the position changes. If a person in motion wishes to maximize their velocity, then that person must

Describing Movement Definitions Acceleration is the rate of change of velocity. TOR C E V Scalar or Vector?

Describing Movement
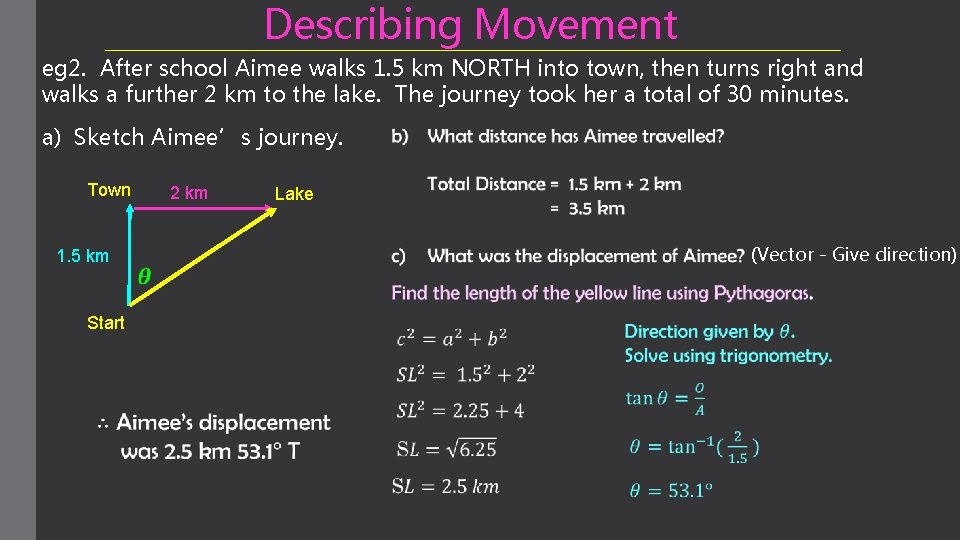
Describing Movement eg 2. After school Aimee walks 1. 5 km NORTH into town, then turns right and walks a further 2 km to the lake. The journey took her a total of 30 minutes. a) Sketch Aimee’s journey. Town 1. 5 km Start 2 km Lake (Vector - Give direction)

Describing Movement Town 1. 5 km Start 2 km Lake b) Total Distance travelled = 3. 5 km

Now Do Chapter 5 – Questions 1, 2, 3, 4, 6, 7, 8, 9, 10

graphs Instantaneous Velocity is the velocity at a particular instant of time. If we plot a graph of an objects Displacement (Position) versus Time, we can find an objects Instantaneous Velocity by calculating the gradient of the graph at a particular point or interval. Similarly, Instantaneous Speed is the speed at a particular instant of time. If we plot a graph of an objects Distance versus Time, we can find an objects Instantaneous Speed by calculating the gradient of the graph at a particular point or interval.

Graphing Motion

Graphing Motion Velocity v Time Graph What are they it? What can we use them for?

Graphing Motion Acceleration v Time Graph What are they it? What can we use them for? • Plot of an objects acceleration (y-axis) versus time (x-axis) • Shows the acceleration of an object over a given period of time • Velocity is found by calculating the area under the graph • If the initial velocity is known, we can use the graph to find the velocity at an instant in time.
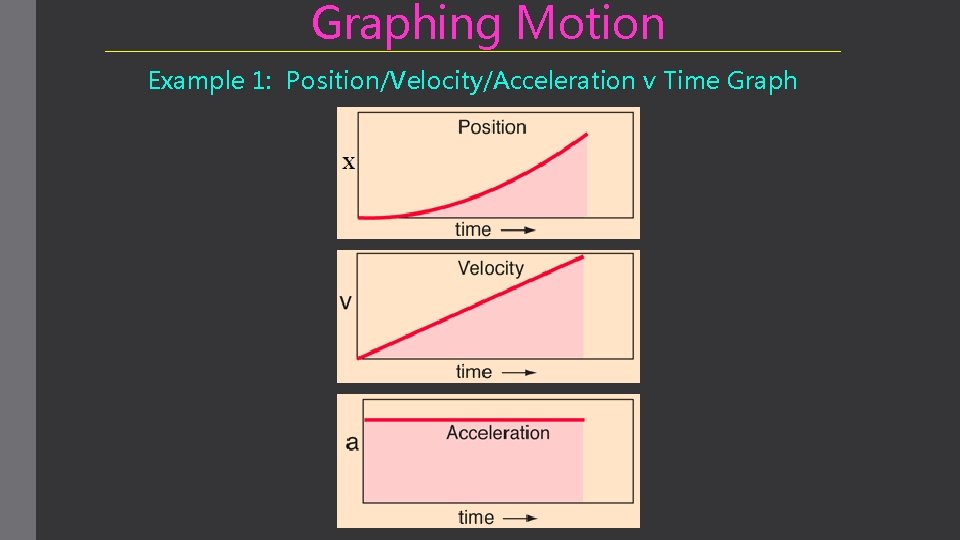
Graphing Motion Example 1: Position/Velocity/Acceleration v Time Graph
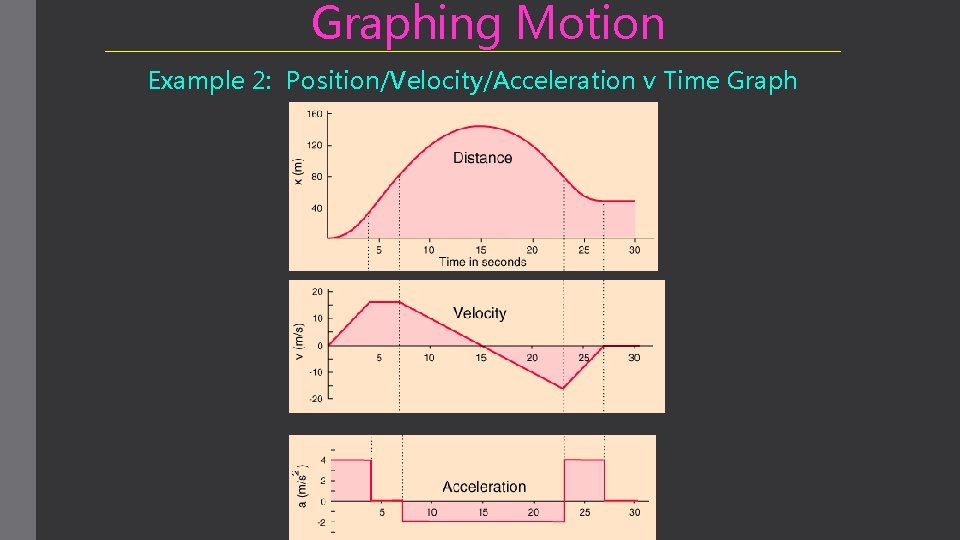
Graphing Motion Example 2: Position/Velocity/Acceleration v Time Graph
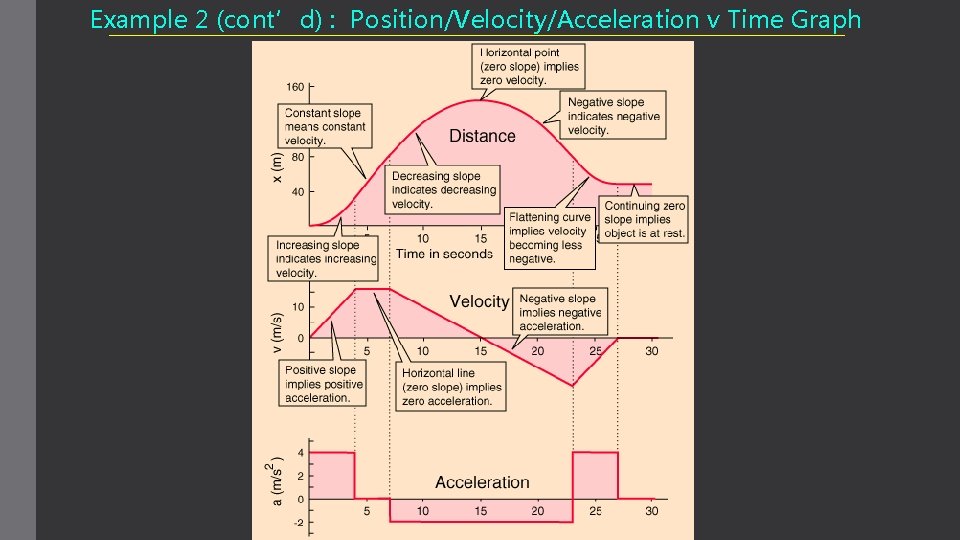
Example 2 (cont’d) : Position/Velocity/Acceleration v Time Graph
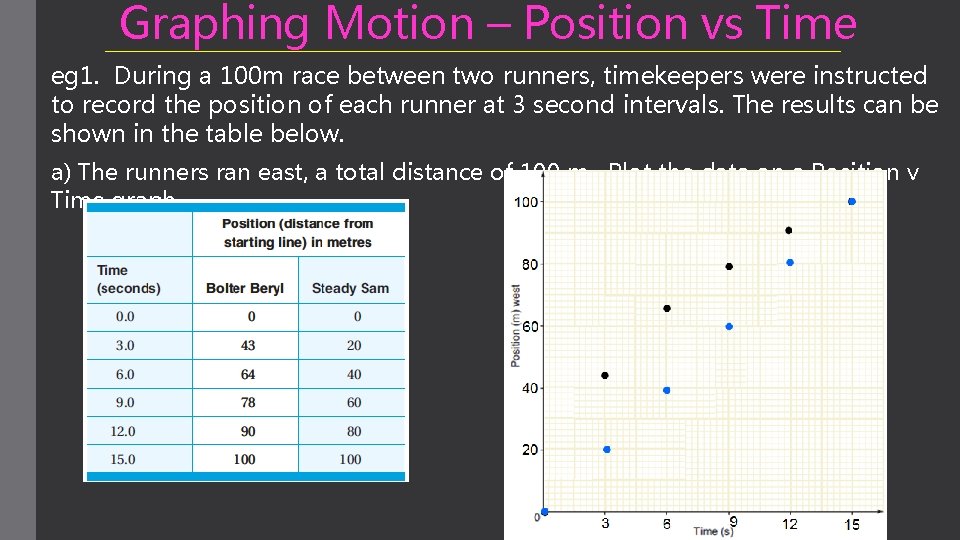
Graphing Motion – Position vs Time eg 1. During a 100 m race between two runners, timekeepers were instructed to record the position of each runner at 3 second intervals. The results can be shown in the table below. a) The runners ran east, a total distance of 100 m. Plot the data on a Position v Time graph
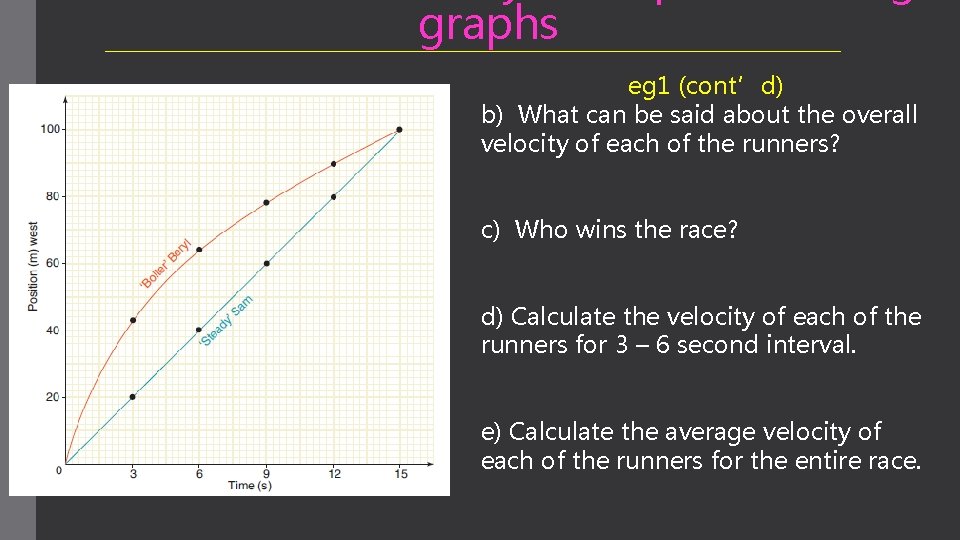
graphs eg 1 (cont’d) b) What can be said about the overall velocity of each of the runners? c) Who wins the race? d) Calculate the velocity of each of the runners for 3 – 6 second interval. e) Calculate the average velocity of each of the runners for the entire race.

graphs
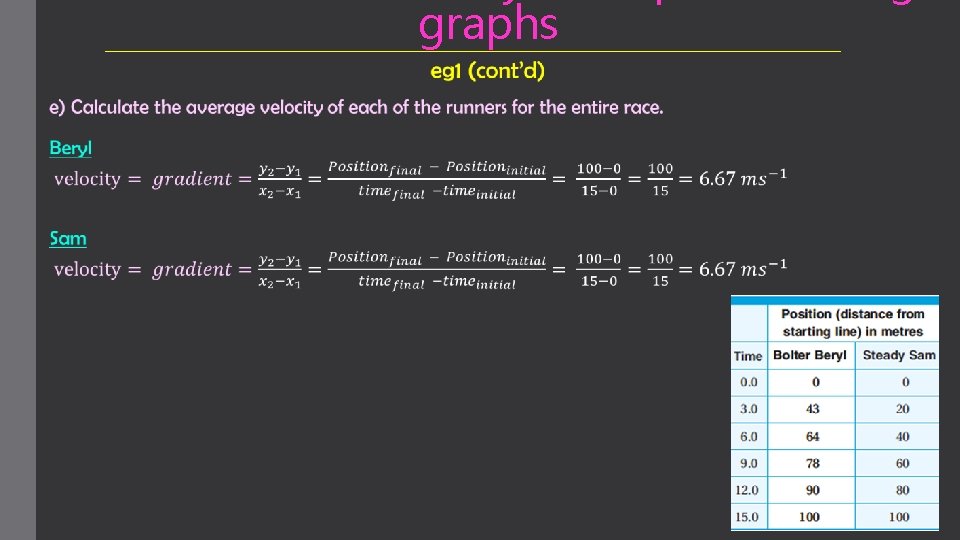
graphs
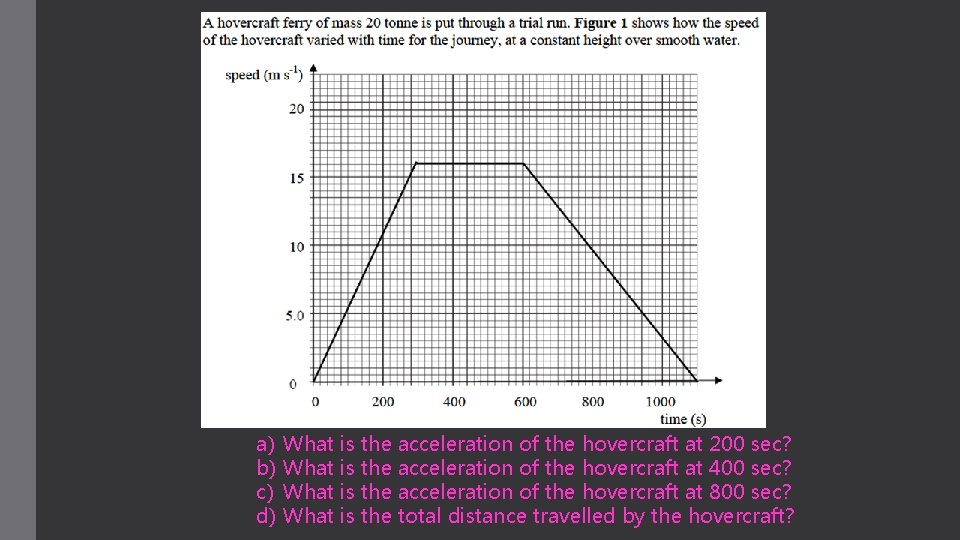
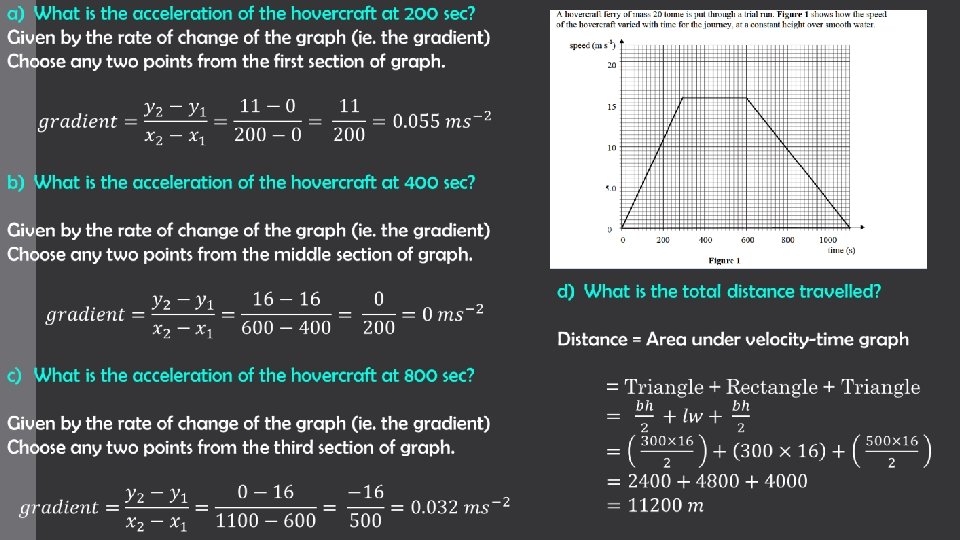
a) b) c) d) What is the acceleration of the hovercraft at 200 sec? What is the acceleration of the hovercraft at 400 sec? What is the acceleration of the hovercraft at 800 sec? What is the total distance travelled by the hovercraft?

Now Do Simulation Activity

Now Do Chapter 5 – Questions 11, 12, 14, 13

Motion Equations – constant acceleration without graphs For straight line motion with constant acceleration, a number of formulae can be used to represent the motion and calculate unknown quantities. The terms which we use in the equations are given by: u = initial velocity (m/s) v = final velocity (m/s) a = acceleration (m/s 2) t = time interval (t) x = displacement (m)

Motion Equations – constant acceleration without graphs

Motion Equations – constant acceleration without graphs eg 1. A coin is dropped into a wishing well and takes 2. 0 s to reach the water. The coin accelerates at a constant 10 m/s 2. Find: a) The coins velocity as it hits the water b) How far does the coin fall before hitting the water?

Motion Equations – constant acceleration without graphs eg 2. A parked car with the handbrake left off rolls down a hill in a straight line with a constant acceleration of 2. 0 m/s 2. It stops after colliding with a brick wall at a speed of 12 m/s. a) For how long was the car rolling? b) How far did the car roll before colliding with the wall?

Now Do Chapter 5 – Questions 21, 22, 23, 24

Force • A force is a push or pull applied by one object on another. • Forces can include: - Actions imposed by people eg. Pushing a door open - Gravity - Friction eg. Resistance caused by rough surfaces - Air Resistance • Force is a vector quantity as it has both a magnitude and direction. • Force is measured in Newtons (N).

Force We can draw diagrams representing forces acting on an object. We represent each force with an arrow. The arrow shows the direction of the force, the length of the arrow indicates its size. An apple falls from a tree. apple? Air Resistance (upward) Weight (downward due to gravitational What forces are acting on the falling
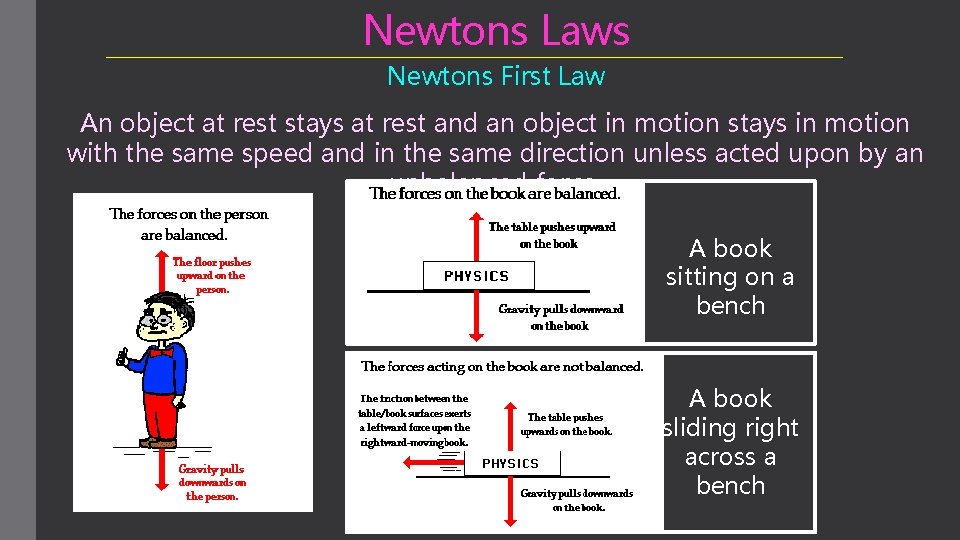
Newtons Laws Newtons First Law An object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force. A book sitting on a bench A book sliding right across a bench

Newtons Laws

Newtons Laws

Newtons Laws

Newtons Laws Newtons Third Law For every action there is an equal and opposite reaction. • If two objects interact with each other, they exert forces upon each other. • Forces always come in pairs - equal and opposite action-reaction force pairs. • The size of the forces on the first object equals the size of the force on the second object. • The direction of the force on the first object is opposite to the direction of the force on the second object. • These two forces are called action and reaction force.

Newtons Laws Newtons Third Law For every action there is an equal and opposite reaction. When you sit in your chair, your body exerts a downward force on the chair and the chair exerts an upward force on your body. There are two forces resulting from this interaction - a force on the chair and a force on your body – the action-reaction forces. We call the reaction forces the ‘Normal’ reaction force.
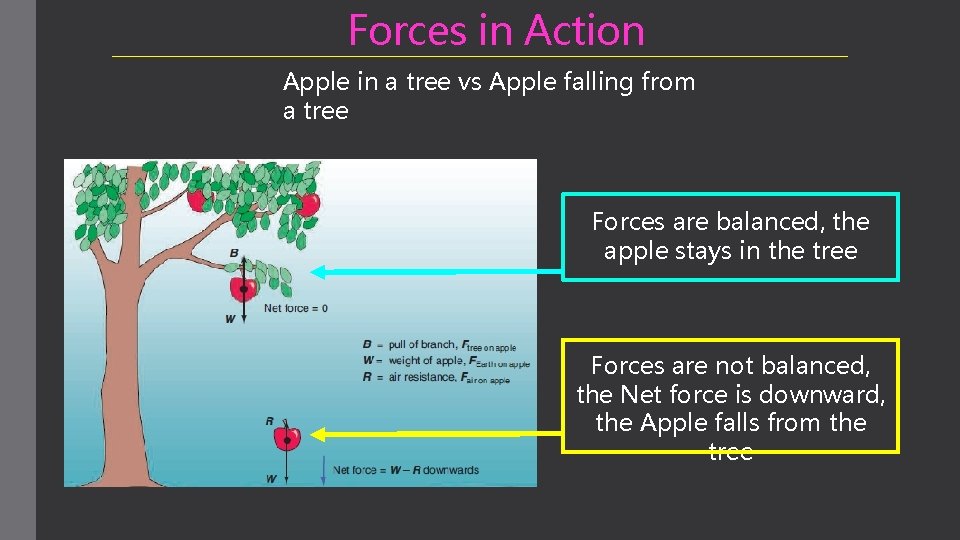
Forces in Action Apple in a tree vs Apple falling from a tree Forces are balanced, the apple stays in the tree Forces are not balanced, the Net force is downward, the Apple falls from the tree

Now Do Chapter 6 – Questions 1, 2, 3, 5, 7

The Net Force
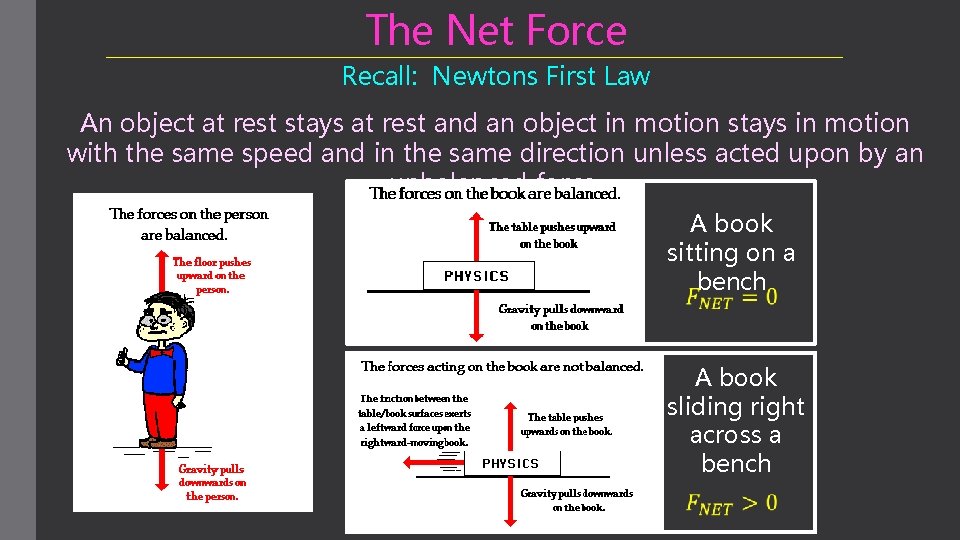
The Net Force Recall: Newtons First Law An object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force. A book sitting on a bench A book sliding right across a bench
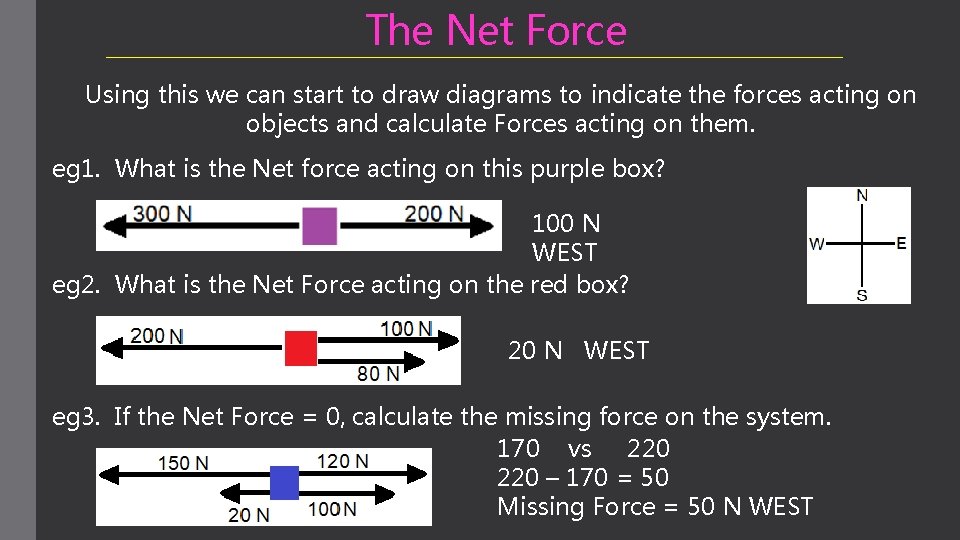
The Net Force Using this we can start to draw diagrams to indicate the forces acting on objects and calculate Forces acting on them. eg 1. What is the Net force acting on this purple box? 100 N WEST eg 2. What is the Net Force acting on the red box? 20 N WEST eg 3. If the Net Force = 0, calculate the missing force on the system. 170 vs 220 – 170 = 50 Missing Force = 50 N WEST

The Net Force

The Net Force
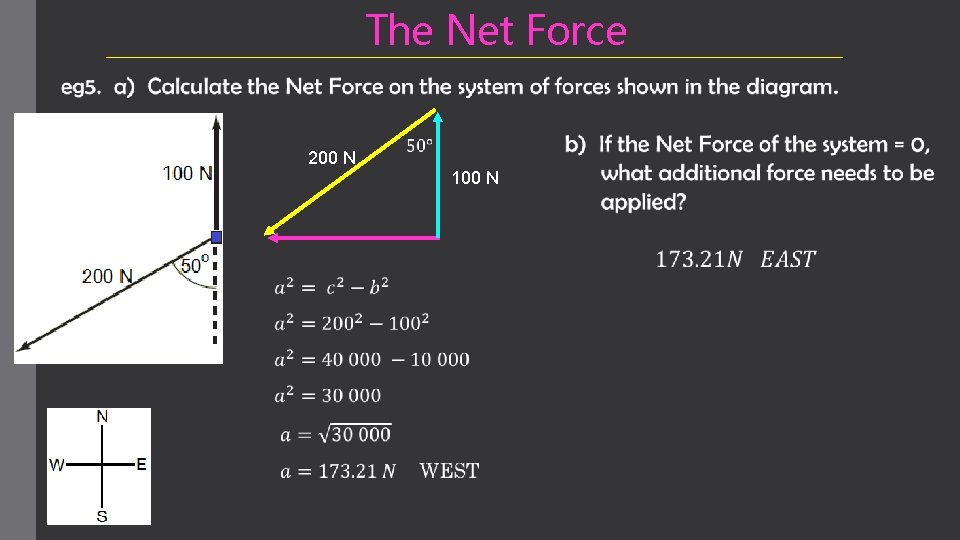
The Net Force 200 N 100 N
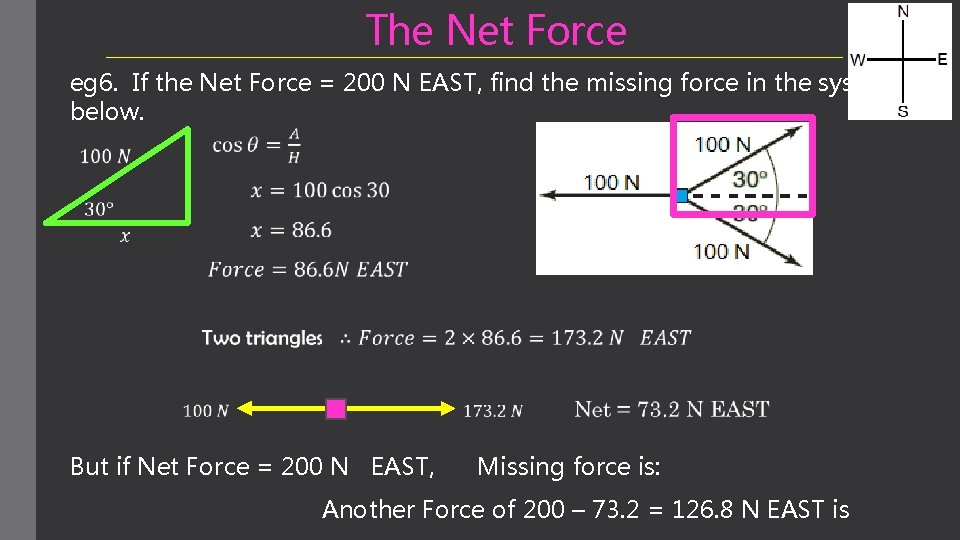
The Net Force eg 6. If the Net Force = 200 N EAST, find the missing force in the system below. But if Net Force = 200 N EAST, Missing force is: Another Force of 200 – 73. 2 = 126. 8 N EAST is

Now Do Chapter 6 – Questions 9, 10, 11
- Slides: 47