Motion of Objects Projected at an Angle www

Motion of Objects Projected at an Angle www. assignmentpoint. com

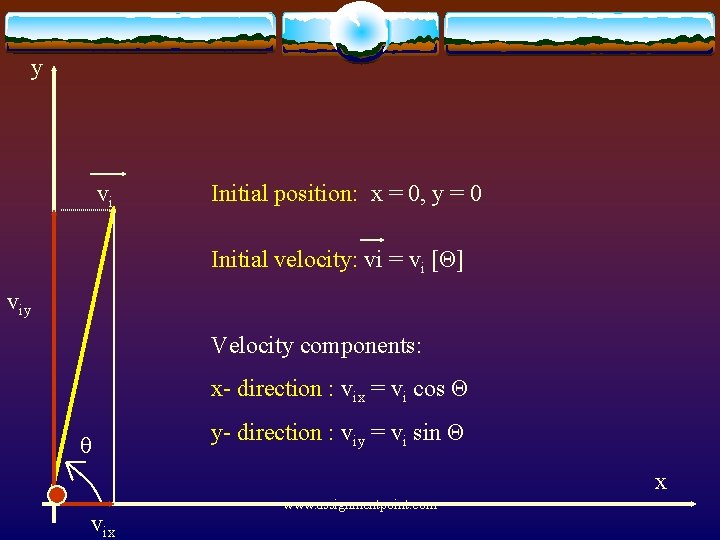
y vi Initial position: x = 0, y = 0 Initial velocity: vi = vi [Θ] viy Velocity components: x- direction : vix = vi cos Θ θ y- direction : viy = vi sin Θ x vix www. assignmentpoint. com

y a =g= - 9. 81 m/s 2 • Motion is accelerated • Acceleration is constant, and downward • a = g = -9. 81 m/s 2 • The horizontal (x) component of velocity is constant • The horizontal and vertical motions are independent of each other, but they have a common time www. assignmentpoint. com x

ANALYSIS OF MOTION: ASSUMPTIONS • x-direction (horizontal): uniform motion • y-direction (vertical): accelerated motion • no air resistance QUESTIONS • What is the trajectory? • What is the total time of the motion? • What is the horizontal range? • What is the maximum height? • www. assignmentpoint. com What is the final velocity?

Equations of motion: X Uniform motion ax = 0 Y Accelerated motion ay = g = -9. 81 m/s 2 VELOCITY vx = vix= vi cos Θ vx = vi cos Θ vy = viy+ g t vy = vi sin Θ + g t DISPLACEMENT x = vix t = vi t cos Θ y = h + viy t + ½ g t 2 x = vi t www. assignmentpoint. com cos Θ y = vi t sin Θ + ½ g t 2 ACCELERATION

Equations of motion: X Uniform motion ax = 0 Y Accelerated motion ay = g = -9. 81 m/s 2 VELOCITY vx = vi cos Θ vy = vi sin Θ + g t DISPLACEMENT x = vi t cos Θ y = vi t sin Θ + ½ g t 2 ACCELERATION www. assignmentpoint. com

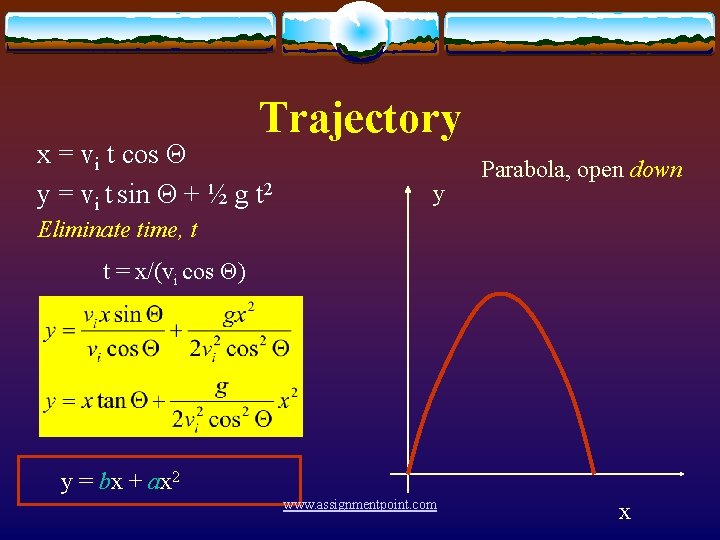
Trajectory x = vi t cos Θ y = vi t sin Θ + ½ g t 2 y Parabola, open down Eliminate time, t t = x/(vi cos Θ) y = bx + ax 2 www. assignmentpoint. com x

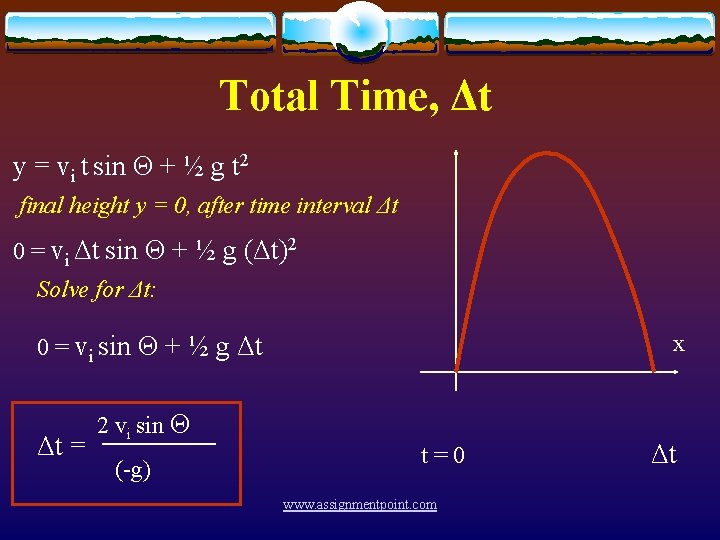
Total Time, Δt y = vi t sin Θ + ½ g t 2 final height y = 0, after time interval Δt 0 = vi Δt sin Θ + ½ g (Δt)2 Solve for Δt: x 0 = vi sin Θ + ½ g Δt Δt = 2 vi sin Θ (-g) t=0 www. assignmentpoint. com Δt

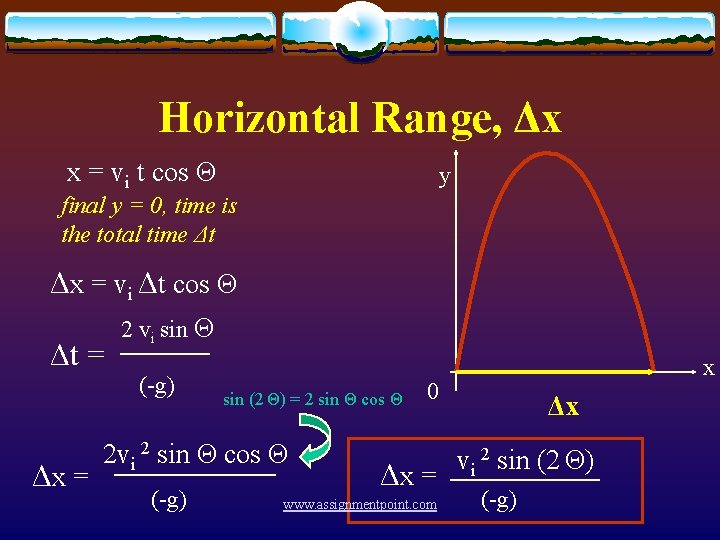
Horizontal Range, Δx x = vi t cos Θ y final y = 0, time is the total time Δt Δx = vi Δt cos Θ Δt = Δx = 2 vi sin Θ (-g) sin (2 Θ) = 2 sin Θ cos Θ 2 vi 2 sin Θ cos Θ (-g) x 0 Δx = www. assignmentpoint. com Δx vi 2 sin (2 Θ) (-g)

Horizontal Range, Δx Δx = Θ (deg) sin (2 Θ) 0 0. 00 15 0. 50 30 0. 87 45 1. 00 60 0. 87 75 0. 50 90 0 vi 2 sin (2 Θ) (-g) • CONCLUSIONS: • Horizontal range is greatest for the throw angle of 450 • Horizontal ranges are the same for angles Θ and (900 – Θ) www. assignmentpoint. com

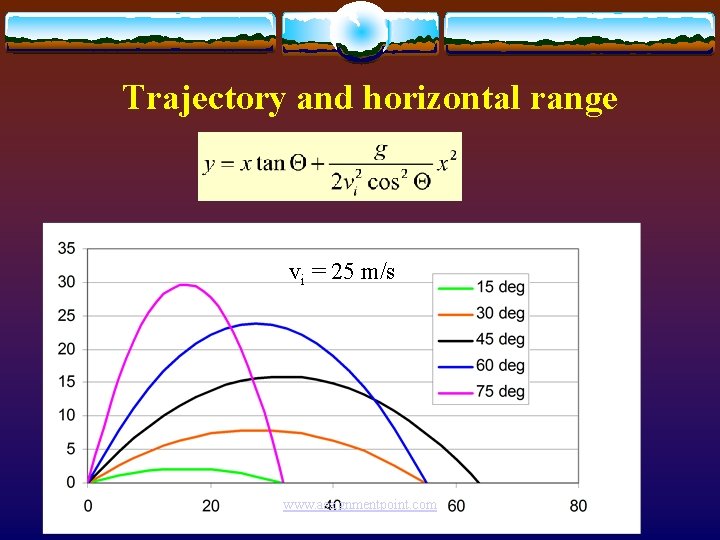
Trajectory and horizontal range vi = 25 m/s www. assignmentpoint. com

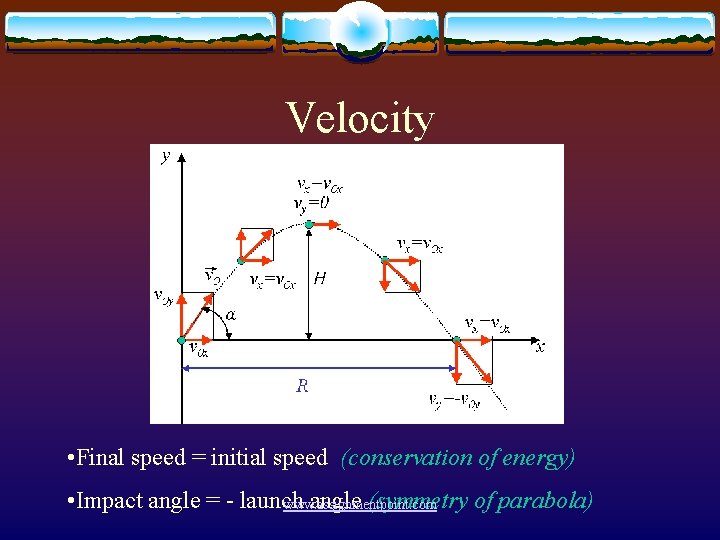
Velocity • Final speed = initial speed (conservation of energy) • Impact angle = - launch angle (symmetry of parabola) www. assignmentpoint. com

Maximum Height vy = vi sin Θ + g t y = vi t sin Θ + ½ g t 2 At maximum height vy = 0 0 = vi sin Θ + g tup = vi sin Θ (-g) tup = Δt/2 hmax = vi t upsin Θ + ½ g tup 2 hmax = vi 2 sin 2 Θ/(-g) + ½ g(vi 2 sin 2 Θ)/g 2 hmax = vi 2 sin 2 Θ 2(-g) www. assignmentpoint. com

Projectile Motion – Final Equations (0, 0) – initial position, vi = vi [Θ]– initial velocity, g = -9. 81 m/s 2 Trajectory Total time Horizontal range Parabola, open down Δt = Δx = 2 vi sin Θ (-g) vi 2 sin (2 Θ) (-g) vi 2 sin 2 Θ Max height hmax =www. assignmentpoint. com 2(-g)