Motion in One Dimension Position l The objects

Motion in One Dimension

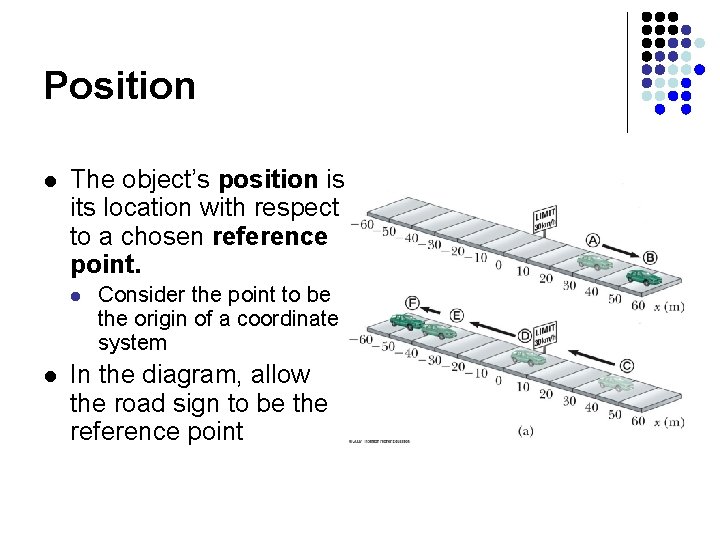
Position l The object’s position is its location with respect to a chosen reference point. l l Consider the point to be the origin of a coordinate system In the diagram, allow the road sign to be the reference point

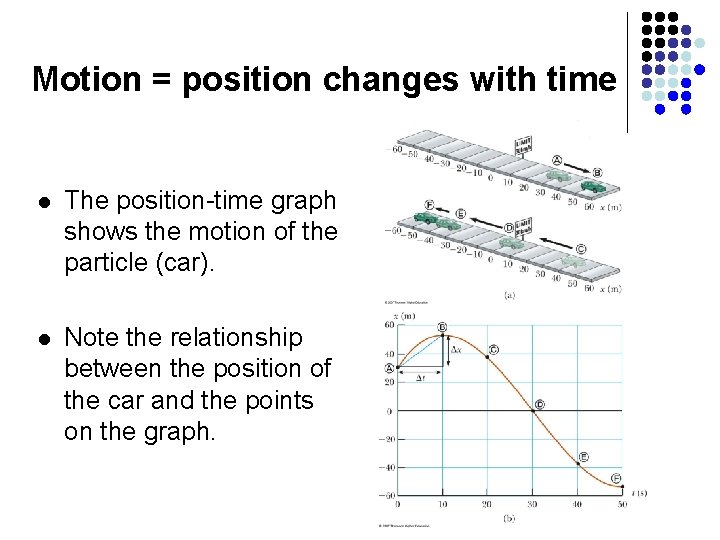
Motion = position changes with time l The position-time graph shows the motion of the particle (car). l Note the relationship between the position of the car and the points on the graph.

Displacement vs. Distance l Displacement: change in position during some time interval. l l Represented as x x ≡ xf - xi SI units are meters (m) x can be positive or negative Distance: the length of a path followed by a particle; always positive.

Average Velocity l The average velocity is the rate at which displacement occurs l l The x indicates motion along the x-axis The dimensions are length / time [L/T] The SI units are m/s. It is also the slope of the line connecting initial and final points on the position – time graph.

Average Speed l Speed is a scalar quantity l l same units as velocity total distance / total time: The average speed has no direction and is always expressed as a positive number. Average velocity and average speed give no details about the trip described.

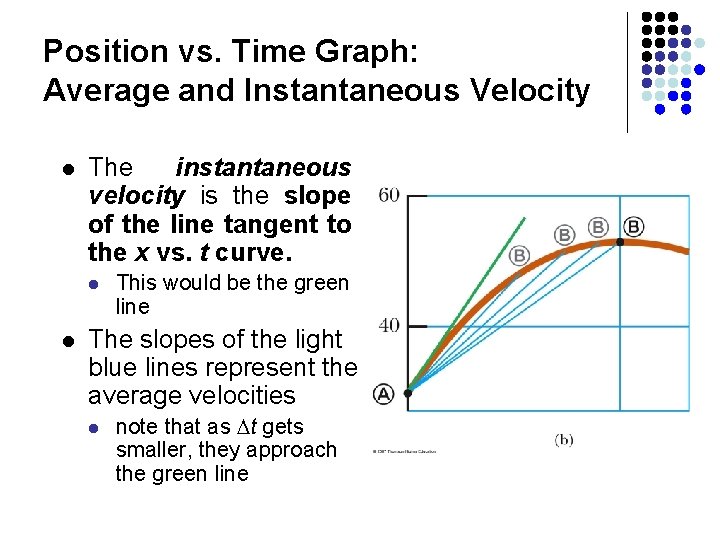
Position vs. Time Graph: Average and Instantaneous Velocity l The instantaneous velocity is the slope of the line tangent to the x vs. t curve. l l This would be the green line The slopes of the light blue lines represent the average velocities l note that as t gets smaller, they approach the green line

Instantaneous Speed l The instantaneous speed is the magnitude of the instantaneous velocity, therefore can not be negative. l The instantaneous speed has no direction associated with it.

Average vs. Instantaneous l Average speed = over a time interval l l Average speed for the whole trip Average speed between t=5 s and t=10 s Slope of secant line on x(t) graph Instantaneous speed = at this moment l l l Speed at t = 8 s Speed at the moment it passed by the police car Slope of tangent line on x(t) graph

Particle Under Constant Velocity l instantaneous velocity at any instant during a time interval is the same as the average velocity during that time interval. l vx = vx, avg The mathematical representation of this situation is the equation l Let ti = 0 and tf = t; the equation becomes: xf = xi + vx t l

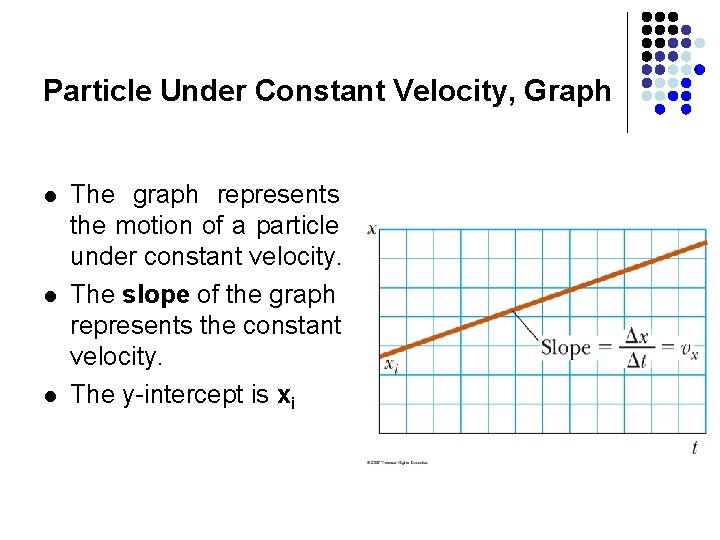
Particle Under Constant Velocity, Graph l l l The graph represents the motion of a particle under constant velocity. The slope of the graph represents the constant velocity. The y-intercept is xi

Particle Under Constant Acceleration

Average Acceleration l Acceleration is the rate of change of the velocity: l SI units are m/s² In one dimension, positive and negative can be used to indicate direction. l

Instantaneous Acceleration l The instantaneous acceleration is the limit of the average acceleration as t approaches 0 l The term acceleration will mean instantaneous acceleration l If average acceleration is wanted, the word average will be included

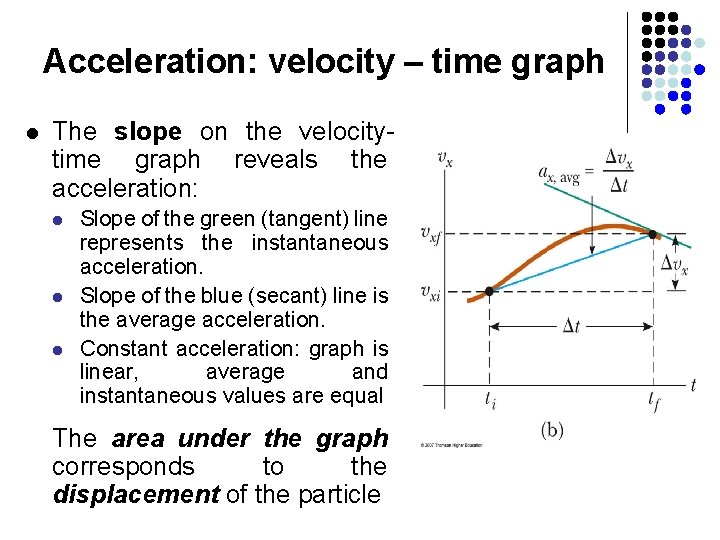
Acceleration: velocity – time graph l The slope on the velocitytime graph reveals the acceleration: l l l Slope of the green (tangent) line represents the instantaneous acceleration. Slope of the blue (secant) line is the average acceleration. Constant acceleration: graph is linear, average and instantaneous values are equal The area under the graph corresponds to the displacement of the particle

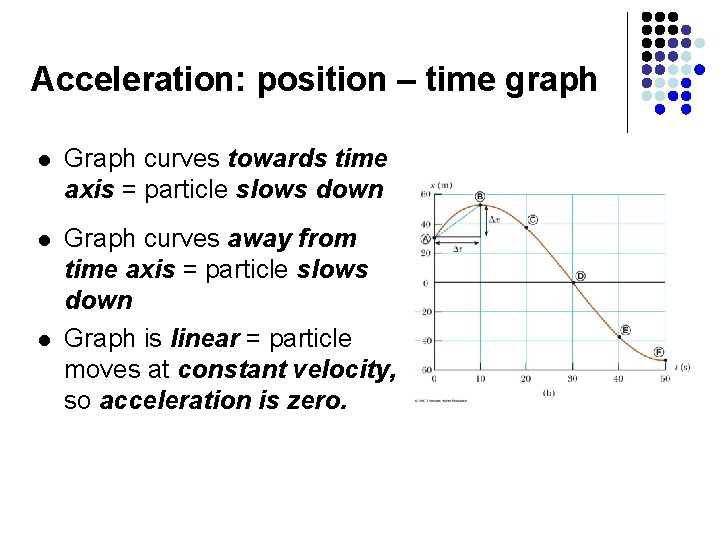
Acceleration: position – time graph l Graph curves towards time axis = particle slows down l Graph curves away from time axis = particle slows down Graph is linear = particle moves at constant velocity, so acceleration is zero. l

Acceleration and Velocity l When an object’s velocity and acceleration are in the same direction, the object is speeding up. l When an object’s velocity and acceleration are in opposite directions, the object is slowing down. l If possible, take initial velocity direction as positive. If not, don’t.

Acceleration and Velocity l l Images are equally spaced. The car is moving with constant positive velocity (shown by red arrows maintaining the same size) Acceleration equals zero

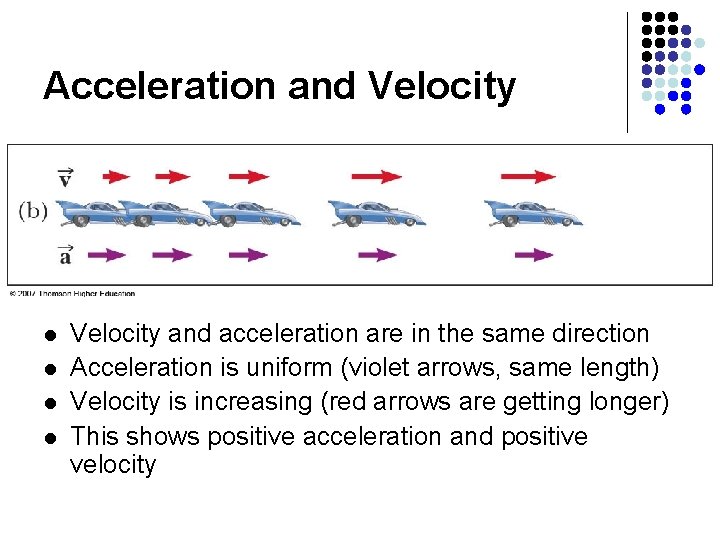
Acceleration and Velocity l l Velocity and acceleration are in the same direction Acceleration is uniform (violet arrows, same length) Velocity is increasing (red arrows are getting longer) This shows positive acceleration and positive velocity

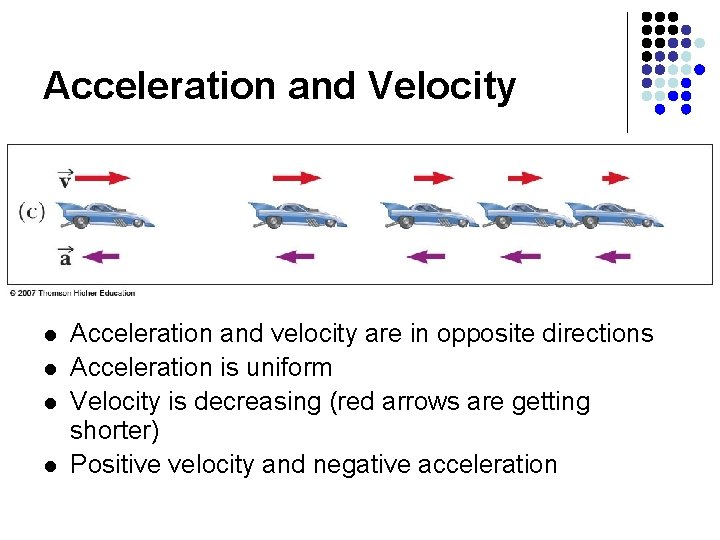
Acceleration and Velocity l l Acceleration and velocity are in opposite directions Acceleration is uniform Velocity is decreasing (red arrows are getting shorter) Positive velocity and negative acceleration

Acceleration and Velocity l In all the previous cases, the acceleration was constant l l Shown by the violet arrows all maintaining the same length The diagrams represent motion of a particle under constant acceleration.

Kinematic Equations – The Big Four

Kinematic Equations l The kinematic equations can be used with any particle under uniform acceleration. l You may need to use two (or more) of the equations to solve one problem. l l x, v, a can be either positive or negative! Many times there is more than one correct way to solve a problem.

Kinematic Equations l For constant acceleration: l Can determine an object’s velocity at any time t when we know its initial velocity and its acceleration. l l Assumes ti = 0 and tf = t Does not give any information about displacement.

Kinematic Equations, specific l For constant acceleration: l The average velocity can be expressed as the arithmetic mean of the initial and final velocities.

Kinematic Equations, specific l For constant acceleration: l This gives you the position of the particle in terms of time and velocities. l Doesn’t give you the acceleration.

Kinematic Equations, specific l For constant acceleration: l Gives final position in terms of velocity and acceleration. l Doesn’t tell you about final velocity.

Kinematic Equations, specific l For constant acceleration: l Gives final velocity in terms of acceleration and displacement. l Does not give any information about the time.

When a = 0 l When the acceleration is zero, l l l vxf = vxi = vx xf = xi + vx t i. e. , constant acceleration includes constant velocity as a special case.

Example l A train starts from rest and moves with constant acceleration. It reaches 30 m/s the moment it has traveled 150 m. Calculate: l The acceleration of the train, and the time it takes to travel the first 150 m; l The time it takes, and the distance it travels between reaching 30 m/s until it reaches 50 m/s.

Free Fall

Galileo Galilei l l 1564 – 1642 Italian physicist and astronomer. l Formulated laws of motion for objects in free fall. l Supported heliocentric universe.

Freely Falling Objects l A freely falling object is moving under the influence of gravity alone. l l We will neglect air resistance. Acceleration does not depend on the launching conditions of the object: l l l Dropped – released from rest Launched downward Launched upward

Acceleration of Freely Falling Object l The acceleration of an object in free fall is directed downward, regardless of the initial motion. l Its magnitude is constant, g = 9. 80 m/s 2 l l g decreases with altitude g varies with latitude, Earth crust composition, etc 9. 80 m/s 2 is the average at the Earth’s surface It doesn’t come with a negative sign included

Acceleration of Free Fall l Free fall motion is constantly accelerated motion in one dimension. l Let upward be positive l Use: l l kinematic equations with ay = -g = - 9. 80 m/s 2

Kinematic Equations – The Big Four

Free Fall: dropped object l Initial velocity is zero l Let up be positive l Use the kinematic equations l l use y instead of x Acceleration is l ay = -g = -9. 80 m/s 2 vo= 0 a=-g

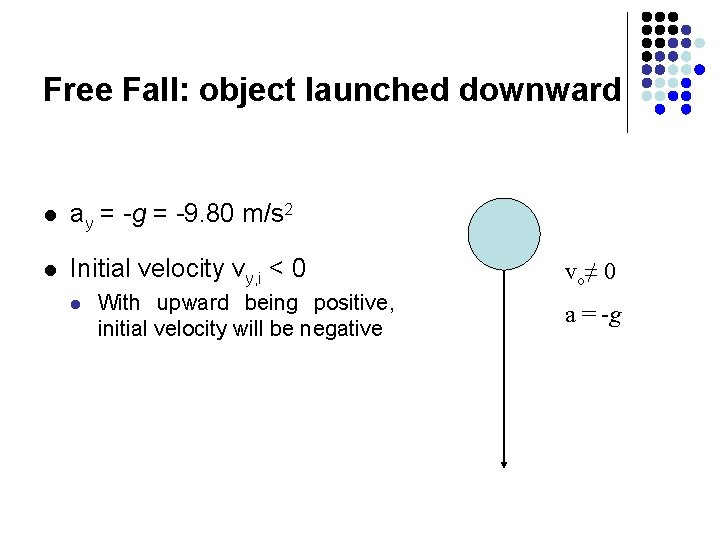
Free Fall: object launched downward l ay = -g = -9. 80 m/s 2 l Initial velocity vy, i < 0 l With upward being positive, initial velocity will be negative vo≠ 0 a = -g

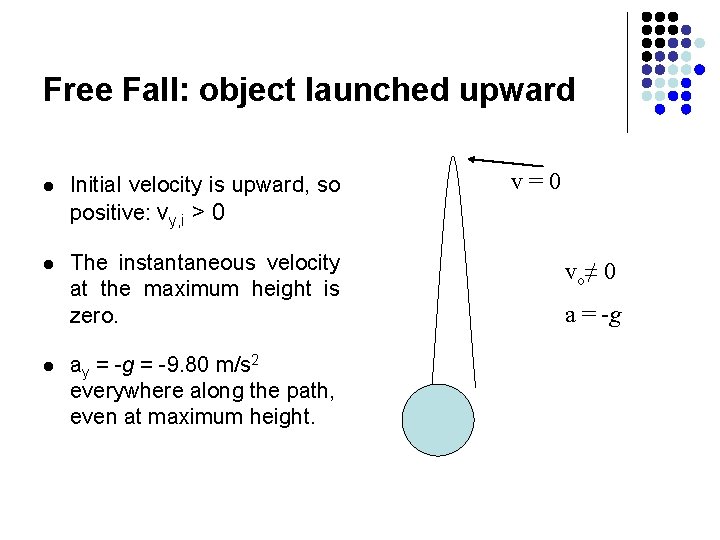
Free Fall: object launched upward l Initial velocity is upward, so positive: vy, i > 0 l The instantaneous velocity at the maximum height is zero. l ay = -g = -9. 80 m/s 2 everywhere along the path, even at maximum height. v=0 vo≠ 0 a = -g

Object Launched Upward. l If the motion is symmetrical, i. e. end point coincides with start point: l l l Then tup = tdown Then vfinal = -vinitial If the motion is not symmetrical: l Break the motion into various parts l Generally up and down

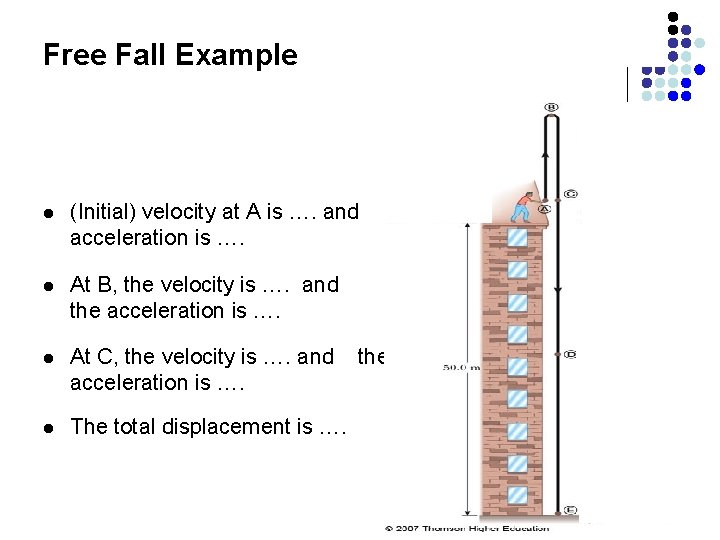
Free Fall Example l (Initial) velocity at A is …. and acceleration is …. l At B, the velocity is …. and the acceleration is …. l At C, the velocity is …. and acceleration is …. l The total displacement is …. the

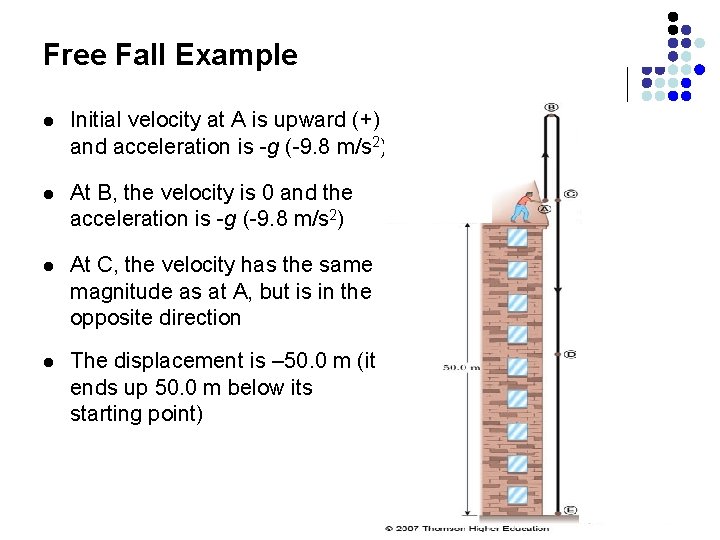
Free Fall Example l Initial velocity at A is upward (+) and acceleration is -g (-9. 8 m/s 2) l At B, the velocity is 0 and the acceleration is -g (-9. 8 m/s 2) l At C, the velocity has the same magnitude as at A, but is in the opposite direction l The displacement is – 50. 0 m (it ends up 50. 0 m below its starting point)