Motion in One Dimension Mechanics Kinematics Describes motion

Motion in One Dimension

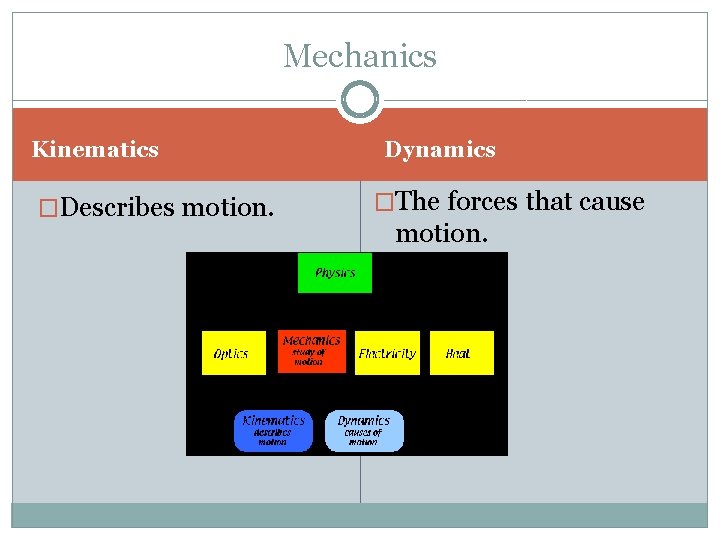
Mechanics Kinematics �Describes motion. Dynamics �The forces that cause motion.

Scalars and Vectors There are two kinds of measurement: scalars and vectors. Scalar – has only magnitude (size), such as distance. Ex. 35 m Vector – has both magnitude and direction, such as position. Ex. 45 km north

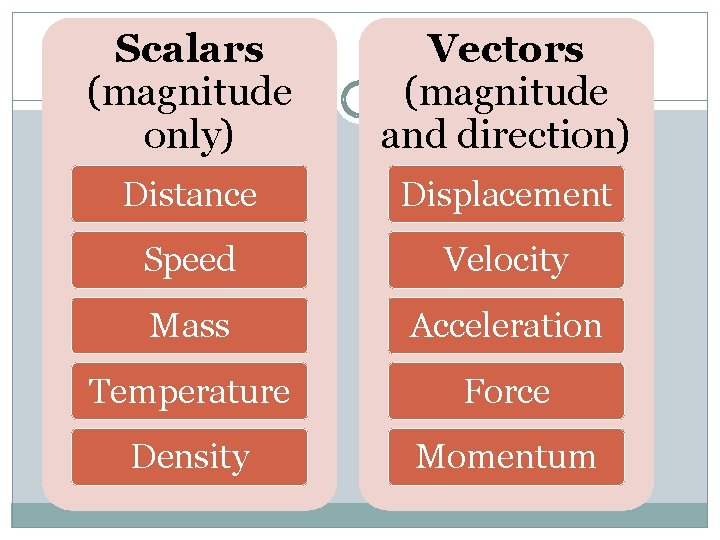
Scalars (magnitude only) Vectors (magnitude and direction) Distance Displacement Speed Velocity Mass Acceleration Temperature Force Density Momentum

A jet airplane travelled at 200 km/hr towards the southwest. This is an example of a 1. Vector 2. Scalar

200 km/hr to the southwest represents … 1. Speed 2. Velocity 3. Distance 4. Acceleration 5. Displacement

Position (x) – the separation between an object and a reference point. - it can be positive or negative depending on which side of the reference point that it is

Motion Anytime an object changes its position (x), it is engaged in motion. Displacement (Δx) = change in position. Δx = xf - xi xf = final position xi = initial position

Distance vs. Displacement �Joe Adams - punt return �Distance (d) = total amount travelled regardless of direction (the real amount that Adams ran); scalar �Displacement (Δx) = the difference between the final and initial position (the yardage that shows up in the box score); vector

Reference Point Reference point (or frame of reference) – a point that you label as zero and measure objects distance from

Average Velocity

Average Velocity Average velocity = change in displacement per unit time __ v = (xf–xi) / (tf–ti) = Δx/Δt = Δx/t xf = position at clock reading t 2 xi = pos. at earlier clock reading t 1 ∆x = xf – xi ∆t = t 2 – t 1

London Olympics and Average Velocity �Pure Speed �Usain Bolt and Average Velocity �In the water. . .

Is Usain Bolt’s average velocity in the 200 m greater, less, or the same as in the 100 m? 1. Greater in the 200 m 2. Less in the 200 m 3. The same in the 200 m (+/- 1 m/s)

Usain Bolt in the 200 m

True or False: A car clocked with an average velocity of 85 mph east must have been moving faster than a car clocked with an average velocity of 75 mph east throughout the entire time interval. 1. True 2. False

It is possible to have a negative velocity. 1. True 2. False

Acceleration �Acceleration – a vector quantity that describes the change in velocity over time �a = Δv/t �SI unit = m/s 2

Position vs. Time Graphs Slope = velocity Straight line (constant slope) = constant velocity Curved line = changing velocity = acceleration

Velocity-Time Graphs Area underneath curve or line = displacement Constant Slope ≠ 0 : constant acceleration Zero slope = constant velocity

Acceleration Time Graphs �Used to visually show changes in acceleration. �Area under line = velocity

A velocity time graph with a slope of 0 is definitely not: 1. Moving 2. Accelerating 3. Moving backwards 4. All of the above

A position time graph with a slope of 0 is definitely 1. Moving 2. Motionless 3. Accelerating 4. Moving backwards 5. Exploding in midair

A position time graph that has is curving upward cannot be: 1. Moving in the 2. 3. 4. 5. positive direction Accelerating Changing velocity At a negative position At a constant speed

A position time graph that is linear with a negative slope describes an object which is: 1. Motionless 2. Accelerating 3. Moving at a constant velocity 4. All of the above

A velocity time graph that is linear could possibly describe an object which is: 1. Motionless 2. Accelerating 3. Moving at a constant velocity 4. All of the above

The area between the line and the x-axis on a velocity time graph represents what? 1. Acceleration 2. Speed 3. Displacement 4. Position

The marble will finish first at the end of which color ramp? (Let the betting begin. ) 1. Red 2. Green 3. Yellow 4. Blue 5. All the same

The marble will complete the race with the least time on which color ramp? 1. Red 2. Green 3. Yellow 4. Blue 5. All the same

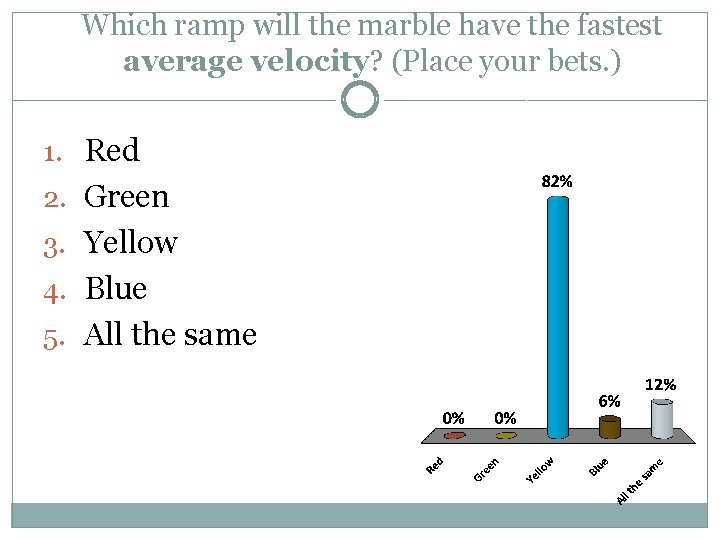
Which ramp will the marble have the fastest average velocity? (Place your bets. ) 1. Red 2. Green 3. Yellow 4. Blue 5. All the same

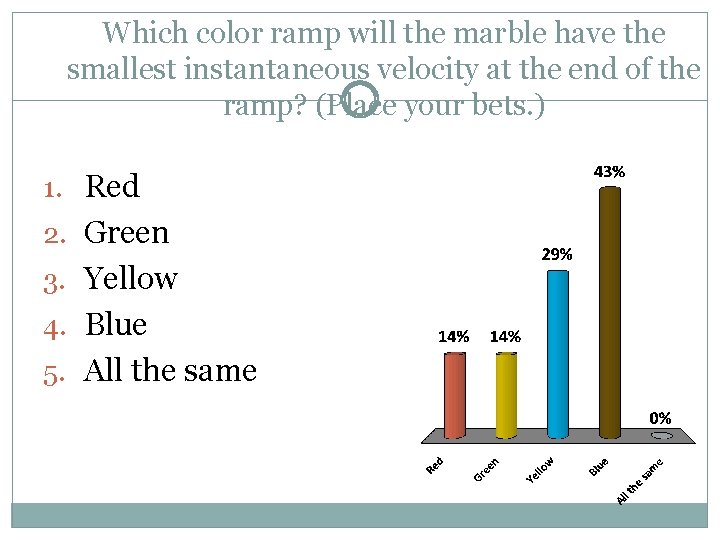
Which color ramp will the marble have the smallest instantaneous velocity at the end of the ramp? (Place your bets. ) 1. Red 2. Green 3. Yellow 4. Blue 5. All the same

Which color ramp will the marble have the largest instantaneous velocity at the end of the ramp? (Place your bets. ) 1. Red 2. Green 3. Yellow 4. Blue 5. All the same

Types of Velocity Constant velocity – this is a situation where the average velocity is the same for all time intervals. Average velocity – takes into account the entire displacement and time; velocity may not always be constant Instantaneous velocity – velocity at a given instant

Acceleration �Acceleration – a vector quantity that describes the change in velocity over time �a = Δv/t = (vf – vi)/t �SI unit = m/s 2

Acceleration �A rocket ship has a negative acceleration but still seems to be speeding up. Is this possible? Justify your answer with concrete details backed up by data.

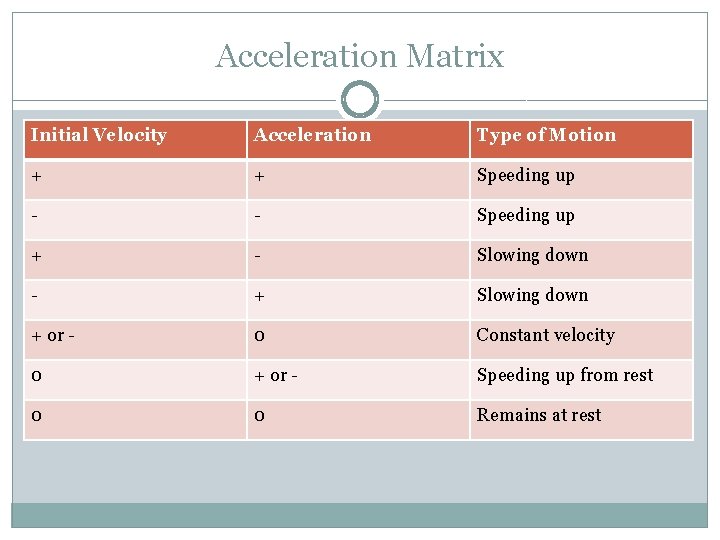
Acceleration Matrix Initial Velocity Acceleration Type of Motion + + Speeding up - - Speeding up + - Slowing down - + Slowing down + or - 0 Constant velocity 0 + or - Speeding up from rest 0 0 Remains at rest

A car speeds up from 10 m/s south to 30 m/s south. Describe the acceleration. 1. Positive 2. Negative 3. Zero 4. Unable to be determined

A cheetah slows down from 10 m/s south to 5 m/s south. Describe the acceleration. 1. Positive 2. Negative 3. Zero 4. Unable to be determined

A minivan slows down from 85 mi/hr to 65 mi/hr when the driver spots a police officer tracking her speed. Describe her acceleration. 1. Positive 2. Negative 3. Zero 4. Unable to be determined

An basketball is released from rest. When the ball hits the ground it is moving at a speed of 8 m/s. Describe the acceleration. 1. Positive 2. Negative 3. Zero 4. Unable to be determined

Tips for Solving Physics Problems � 1) List all given information including unknown variable. Look for any inconsistent units (ex. cm and m/s) If all values are in SI units to start with, the final value will be an SI unit. � 2) List formulas that will be used to solve the problem (before plugging in data). � 3) Plug in data and solve for unknown. � 4) Box your answer and make sure the correct unit is present

Δx t vf vi a EQUATIONS OF MOTION AT CONSTANT ACCELERATION