Motion in a vertical circle Motion in a

Motion in a vertical circle

Motion in a vertical circle: Demo - cup and plate Concept 0: ac > 9. 81 m/s/s so the string stays taut. Example - What is the minimum speed at the top for my bucket if r = 1. 12 m? (So the cup does not fall off) a = v 2/r 9. 81 m/s/s = v 2/(1. 12 m) v ≈ 3. 31 m/s

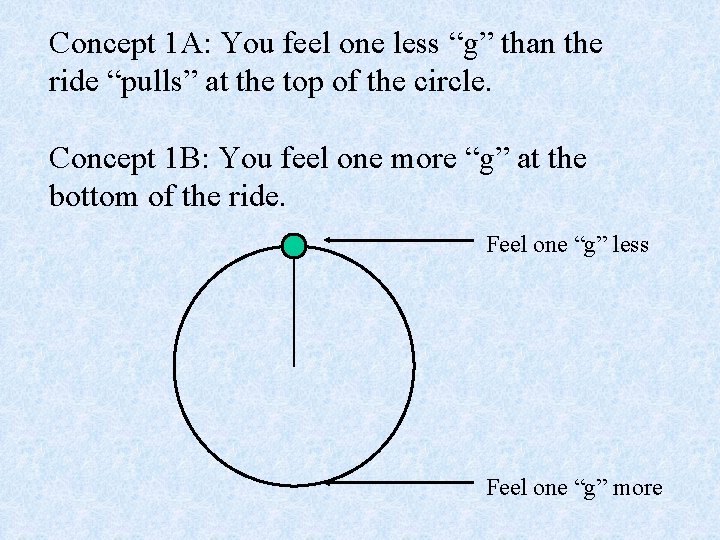
Concept 1 A: You feel one less “g” than the ride “pulls” at the top of the circle. Concept 1 B: You feel one more “g” at the bottom of the ride. Feel one “g” less Feel one “g” more

Ferris Wheel at Oaks Park!!!

Rock-O-Plane

A rider moving in a 3. 75 m radius vertical circle feels 1. 2 “g”s at the top of the circle. A) How many “g”s is the ride pulling? B) How many “g”s do they feel at the bottom? C) What is their tangential velocity? A) - The ride is “pulling one more “g” than 1. 2 or 2. 2 “g”s B) At the bottom you would feel one more “g” than the ride is pulling or 2. 2 + 1 = 3. 2 “g”s C) ac = (2. 2)(9. 81 m/s/s) = 21. 582 m/s/s ac = v 2/r 21. 582 m/s/s = v 2/(3. 75 m), v = 8. 9962 ≈ 9. 0 m/s Feel one 1. 2 “g”s (one less than the ride) Feel one “g” more than the ride

Whiteboards: Motion in a vertical circle 1|2|3|4 TOC

What is the maximum radius you can twirl a bucket full of water going 2. 3 m/s at the top? a = v 2/r 9. 81 m/s/s = (2. 3 m/s)2/r r = 0. 539245668 ≈ 0. 54 m W

If a roller coaster pulls 2. 5 “g”s in a vertical circle, what do you feel at the top of the loop, and at the bottom? (2 answers) Top = 2. 5 - 1 = 1. 5 “g”s Bottom = 2. 5 + 1 = 3. 5 “g”s 1. 5 “g”s, and 3. 5 “g”s W

You feel 2. 1 “g”s at the bottom of a roller coaster loop. What is the ride “pulling” and what do you feel at the top? Ride pulls one less than what you feel or 1. 1 “g”s At the top you would feel one less than that or. 1 “g”s 1. 1 “g”s and. 1 “g”s W

What is your centripetal acceleration if at the top of a roller coaster loop you read. 75 “g”s? The ride is pulling one more than. 75 = 1. 75 “g”s W

What is your speed at the top of a roller coaster loop if you read. 75 “g”s and the loop has a radius of 3. 8 m? (1) The ride is pulling one more than. 75: 1. 75 “g”s a = (1. 75)(9. 81 m/s/s) = 17. 1675 m/s/s a = v 2/r 17. 1675 m/s/s = v 2/(3. 8 m) v = 8. 076911538 ≈ 8. 1 m/s W

Example – O – Rama: A 5. 00 kg object goes 9. 00 m/s in a 3. 75 m radius vertical circle. Find the force needed at the top, and at the bottom. 1. ac = v 2/r = (9. 0 m/s)2/(3. 75) = 21. 6 m/s/s 2. F = ma at top. Forces = weight, and tension, a is down (-) 3. F = ma at bottom, same forces, a is up (+) 4. Voodoo way: Feel one “g” less than the ride Feel one “g” more than the ride

An 9. 0 kg mass moves at a uniform speed of 4. 0 m/s in a 2. 0 m radius circle on the end of a rod. What force is needed at the top and at the bottom? ac = v 2/r = (4. 0 m/s)2/(2. 0 m) = 8. 0 m/s/s weight = mg = (9. 0 kg)(9. 8 N/kg) = 88. 2 N Top <T - 88. 2 N> = (9. 0 kg)(-8. 0 m/s/s) Bottom <T - 88. 2 N> = (9. 0 kg)(+8. 0 m/s/s) or voodoo = at top 9. 8 less than 8. 0 = -1. 8(9) = 16 N bottom one g more, 8+9. 8 = 17. 8(9) Top = 16 N up Bottom = 160 N up W

A 1. 15 kg mass moves at a uniform speed in a 3. 78 m radius circle on the end of a rod. At the top, the rod is exerting a downward force of 5. 02 N on the mass. a) What is the centripetal acceleration of the mass? b) What is its speed? c) What force does the rod exert at the bottom? weight = mg = (1. 15 kg)(9. 81 N/kg) = 11. 2815 N a) Top: <-5. 02 N - 11. 2815 N> = (1. 15 kg)a, a = -14. 175 m/s/s b) ac = v 2/r, 14. 175 m/s/s = v 2/(3. 78 m), v = 7. 3200 m/s c) Bottom: <T - 11. 2815 N> = (1. 15 kg)(+14. 175 m/s/s), T = 27. 583 N ≈ 27. 6 N 14. 2 m/s/s, 7. 32 m/s, 27. 6 N W