Motion in a circle As an object moves

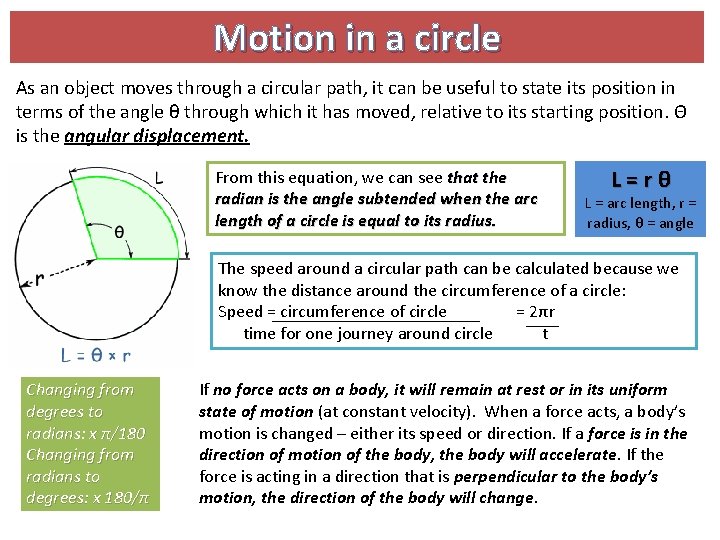
Motion in a circle As an object moves through a circular path, it can be useful to state its position in terms of the angle θ through which it has moved, relative to its starting position. Θ is the angular displacement. From this equation, we can see that the radian is the angle subtended when the arc length of a circle is equal to its radius. L=rθ L = arc length, r = radius, θ = angle The speed around a circular path can be calculated because we know the distance around the circumference of a circle: Speed = circumference of circle = 2πr time for one journey around circle t Changing from degrees to radians: x π/180 Changing from radians to degrees: x 180/π If no force acts on a body, it will remain at rest or in its uniform state of motion (at constant velocity). When a force acts, a body’s motion is changed – either its speed or direction. If a force is in the direction of motion of the body, the body will accelerate. If the force is acting in a direction that is perpendicular to the body’s motion, the direction of the body will change.

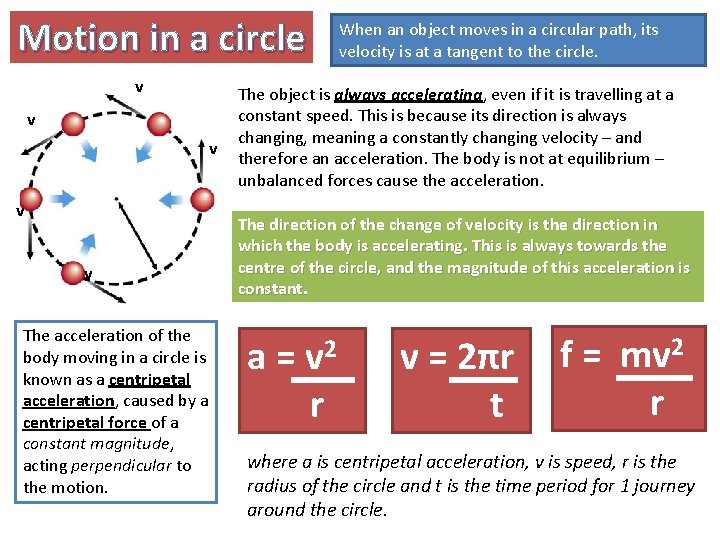
Motion in a circle v v v The acceleration of the body moving in a circle is known as a centripetal acceleration, caused by a centripetal force of a constant magnitude, acting perpendicular to the motion. When an object moves in a circular path, its velocity is at a tangent to the circle. The object is always accelerating, even if it is travelling at a constant speed. This is because its direction is always changing, meaning a constantly changing velocity – and therefore an acceleration. The body is not at equilibrium – unbalanced forces cause the acceleration. The direction of the change of velocity is the direction in which the body is accelerating. This is always towards the centre of the circle, and the magnitude of this acceleration is constant. a= v 2 r v = 2πr t f = mv 2 r where a is centripetal acceleration, v is speed, r is the radius of the circle and t is the time period for 1 journey around the circle.

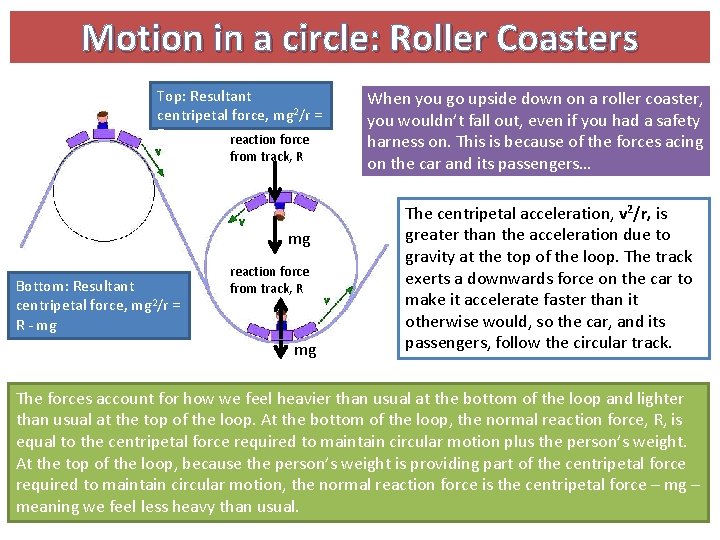
Motion in a circle: Roller Coasters Top: Resultant centripetal force, mg 2/r = R + mg reaction force from track, R mg Bottom: Resultant centripetal force, mg 2/r = R - mg reaction force from track, R mg When you go upside down on a roller coaster, you wouldn’t fall out, even if you had a safety harness on. This is because of the forces acing on the car and its passengers… The centripetal acceleration, v 2/r, is greater than the acceleration due to gravity at the top of the loop. The track exerts a downwards force on the car to make it accelerate faster than it otherwise would, so the car, and its passengers, follow the circular track. The forces account for how we feel heavier than usual at the bottom of the loop and lighter than usual at the top of the loop. At the bottom of the loop, the normal reaction force, R, is equal to the centripetal force required to maintain circular motion plus the person’s weight. At the top of the loop, because the person’s weight is providing part of the centripetal force required to maintain circular motion, the normal reaction force is the centripetal force – mg – meaning we feel less heavy than usual.