Motion in 2 Dimensions Chapter 7 Intro All


















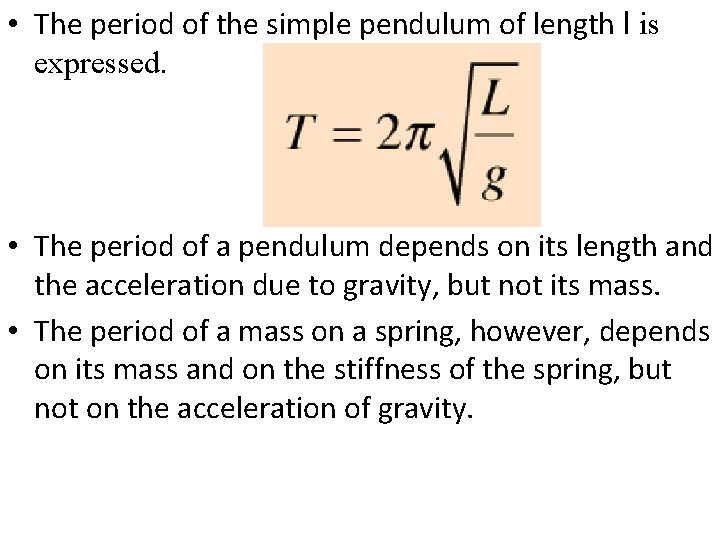



- Slides: 30

Motion in 2 Dimensions Chapter 7

Intro: • All curved motion is the result of a force that causes an object to deviate from its straight-line motion. – According to Newton’s first law of motion, this is caused by an unbalanced force. • From this we can conclude that an object moving in a curved path must be acted upon by a net force. – The curved path depends only upon the direction and size of the unbalanced force acting on the object.

7: 1 Projectiles • Projectile: Any object that is thrown or otherwise projected into the air. – The characteristic path followed by a projectile is a parabola and is called its trajectory. – Projectile motion describes the movement of a projectile along its trajectory.

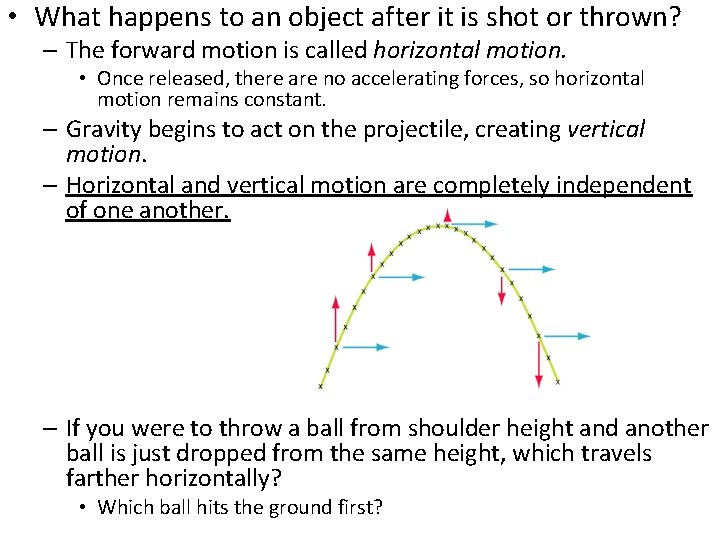
• What happens to an object after it is shot or thrown? – The forward motion is called horizontal motion. • Once released, there are no accelerating forces, so horizontal motion remains constant. – Gravity begins to act on the projectile, creating vertical motion. – Horizontal and vertical motion are completely independent of one another. – If you were to throw a ball from shoulder height and another ball is just dropped from the same height, which travels farther horizontally? • Which ball hits the ground first?


• Horizontal displacement depends on the horizontal velocity and the interval of time that the projectile is in the air. – The projectile’s initial vertical velocity and the acceleration of gravity determine time interval, which can be found using: dv = ½ gt 2 + vit – The horizontal displacement is equal to the product of the horizontal velocity and the time of fall d h = vht dh = horizontal displacement vh = horizontal velocity dv = vertical distance (usually negative)

Example: • A stone is thrown horizontally at 15 m/s. It is thrown from the top of a cliff 44 m high. A. How long does it take the stone to reach the bottom of the cliff? B. How far from the base of the cliff does the stone strike the ground?

Assignment: • P. 116 #1 -6

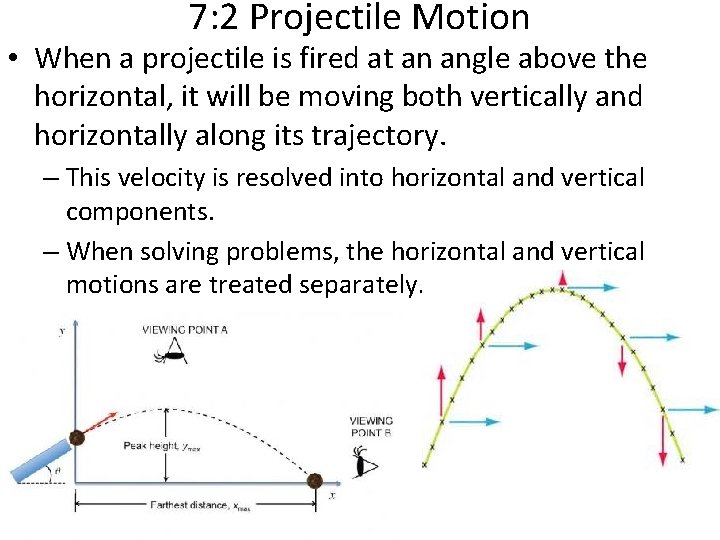
7: 2 Projectile Motion • When a projectile is fired at an angle above the horizontal, it will be moving both vertically and horizontally along its trajectory. – This velocity is resolved into horizontal and vertical components. – When solving problems, the horizontal and vertical motions are treated separately.

Example: • A golf ball is hit and leaves the tee with a velocity of 25. 0 m/s at 35. 0° with respect to the horizontal. What is the horizontal displacement of the ball?

Practice and HW • Practice: Pg. 117 # 7 -8 • HW Pg. 117 #9 -11

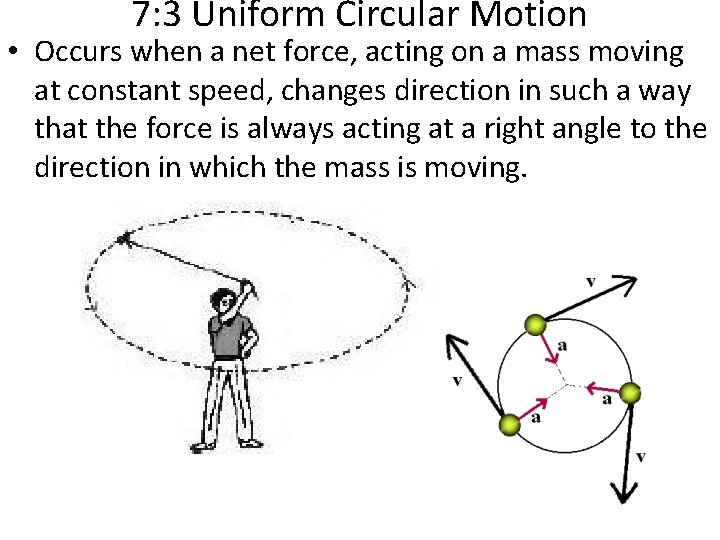
7: 3 Uniform Circular Motion • Occurs when a net force, acting on a mass moving at constant speed, changes direction in such a way that the force is always acting at a right angle to the direction in which the mass is moving.

• Suppose a hand-controlled object is attached to a string and moves in a horizontal circle. – Your hand pulls on the strings and provides an inward radial force that keeps the object moving in its circular path. • This force is called centripetal force, Fc. • Centripetal = center-seeking.

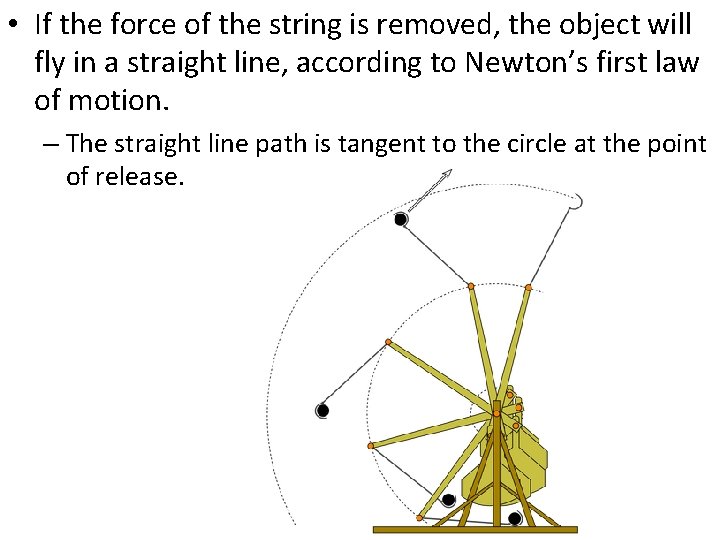
• If the force of the string is removed, the object will fly in a straight line, according to Newton’s first law of motion. – The straight line path is tangent to the circle at the point of release.

• Centripetal force always acts at a right angle to the instantaneous velocity of the object. – Centripetal force cannot change the magnitude of the velocity, just the direction. – Since velocity is a vector quantity, a change in direction is a change in velocity, Δv. • The change in velocity Δv, can be found by subtracting the 2 vectors. (vectors are subtracted by placing them tail-to-tail). Δv = v 2 – v 1 – Fc is always directed toward the center of the circle, as is the centripetal acceleration.

• Centripetal acceleration ac = v 2/r • For magnitude of centripetal force Fc = mv 2/r aka F=mac

Example: Centripetal Acceleration and Force • A 0. 25 -kg mass is attached to a 1. 00 -m length of string. The mass completes a horizontal circle in 0. 42 s. a. What is the velocity of the mass? b. What is the centripetal force acting on the mass?

• Practice: p. 122 #12 -13 • HW: p. 122 -123 #14 -16

7: 4 Placing a Satellite in Orbit • Due to the shape and rotation of the Earth, an object with a horizontal speed of 8. 00 x 103 m/s will remain the same altitude if air resistance is ignored. – In space, there is very little friction, allowing satellites to orbit for long periods of time. – The force of gravity on a satellite, its weight, provides the centripetal force to maintain its circular motion. • Since F = ma and Fc = mv 2/r, mg=mv 2/r. • Because of this, the velocity a satellite must have to orbit the earth is v = √(gr) Where g = acceleration of gravity at distance r.

• A satellite farther from the earth has a larger velocity. • The velocity of a satellite is independent of its mass • A satellite must be given a large velocity to place it into orbit

• HW practice: Pg. 124 #18 -20

7: 5 Simple Harmonic Motion • An object with vibrational motion moves back and forth over the same path. – Examples: A swinging pendulum and vibrating guitar strings. • In simple harmonic motion, SHM, the motion of the object repeats a pattern. – This repeated pattern is called a cycle. – Time to complete one cycle is called a period, T. – The number of cycles completed in a given time interval is called frequency, f. T = 1/f

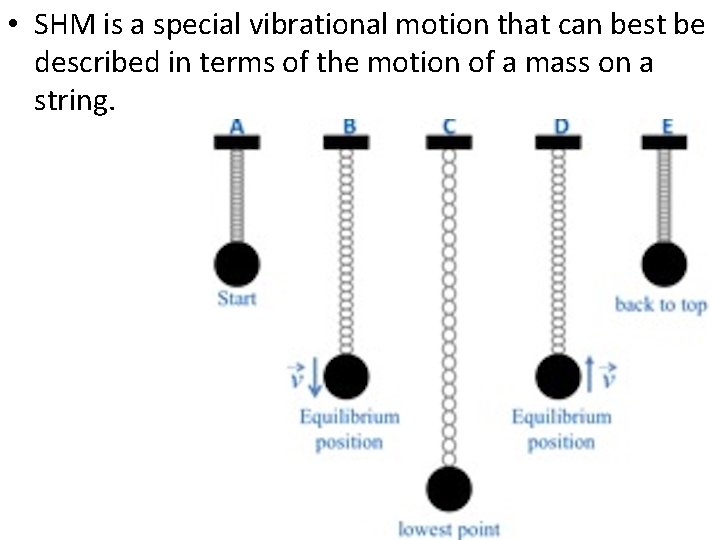
• SHM is a special vibrational motion that can best be described in terms of the motion of a mass on a string.

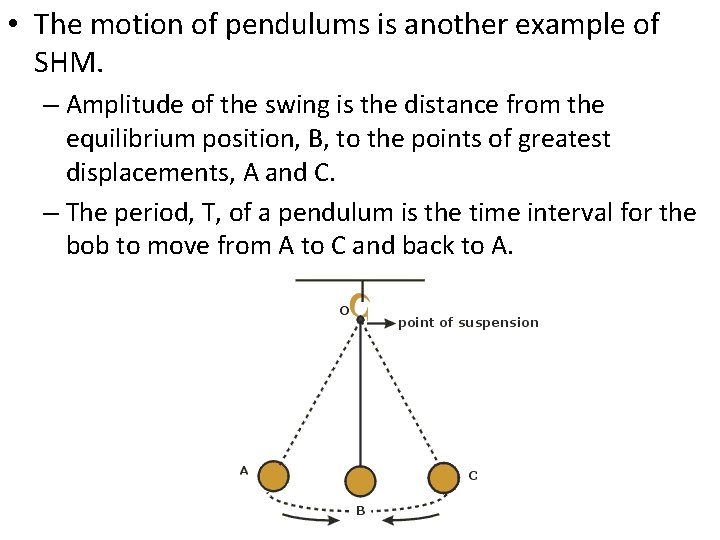
• The motion of pendulums is another example of SHM. – Amplitude of the swing is the distance from the equilibrium position, B, to the points of greatest displacements, A and C. – The period, T, of a pendulum is the time interval for the bob to move from A to C and back to A.

Wavelength = Period

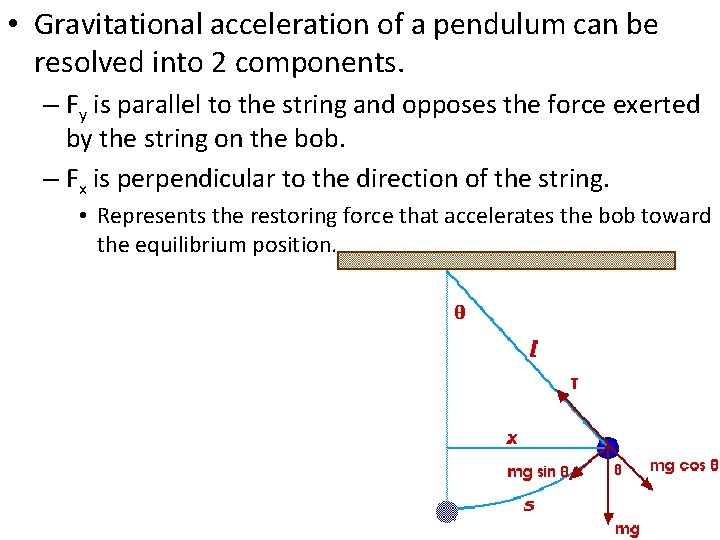
• Gravitational acceleration of a pendulum can be resolved into 2 components. – Fy is parallel to the string and opposes the force exerted by the string on the bob. – Fx is perpendicular to the direction of the string. • Represents the restoring force that accelerates the bob toward the equilibrium position.
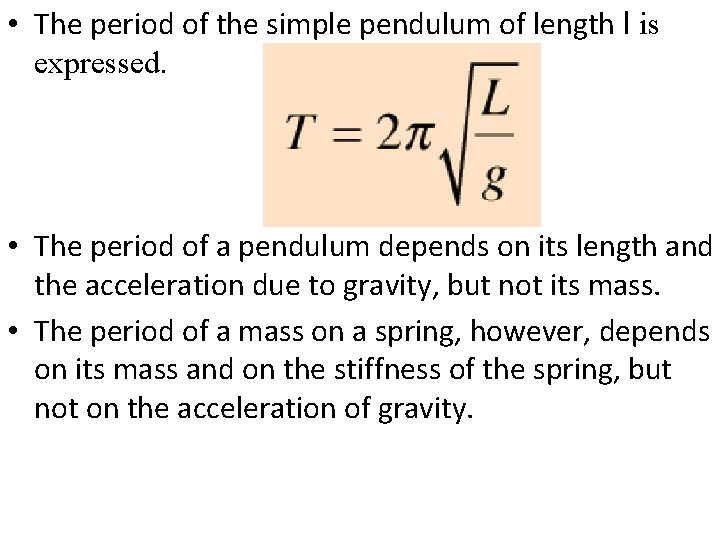
• The period of the simple pendulum of length l is expressed. • The period of a pendulum depends on its length and the acceleration due to gravity, but not its mass. • The period of a mass on a spring, however, depends on its mass and on the stiffness of the spring, but not on the acceleration of gravity.

• The amplitude of any vibrating object can be greatly increased by applying a small external force at the same frequency as the vibrating object. – This effect is called resonance. • Example = “pumping”

Example: • Suppose the period of the movement of a pendulum lasts 1. 2 s on Earth. A. What is the length of the arm on the pendulum? B. Suppose this pendulum were placed on the surface of the moon, whose acceleration of gravity is 1. 6 m/s 2. What is the new period of the pendulum?

Chapter Review • Pg. 130 #6 Pg. 130 problems A #1 -8 • Pg. 131 problems B #1 -2