Motion Chapter 1 Chapters Objectives To introduce the

Motion Chapter 1

Chapter’s Objectives • To introduce the properties of motion (position, speed and velocity, and acceleration) • To introduce types of motion • To use the metric (or SI) system of measurement and to learn how to convert units • To differentiate between speed and velocity. • To differentiate between velocity and acceleration. • To learn how to analyze problem statements and to translate the information into a recipe, and • To develop a problem solving skill • To learn how to convert units

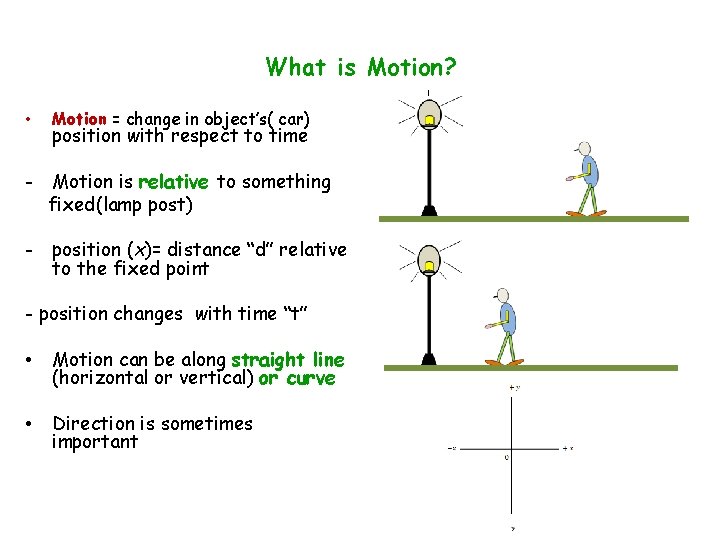
What is Motion? • Motion = change in object’s( car) position with respect to time - Motion is relative to something fixed(lamp post) - position (x)= distance “d” relative to the fixed point - position changes with time “t” • Motion can be along straight line (horizontal or vertical) or curve • Direction is sometimes important

Scalars and Vectors Scalar = physical quantity that has magnitude only • Examples: Mass, length, speed, time, temperature • described by a number and unit only (speed is 5 m/sec) vector =physical quantity that has both magnitude and direction • Examples: weight, force, velocity, acceleration • Described by a number, unit, and Direction (velocity is 5 m/sec NE) • Arrow is used for direction

Measurement = comparing a quantity like length, mass, … to a standard or unit like meter for example Four steps for a measurement • Select a standard unit of measurement (m, sec, kg, …) • Follow a procedure or operation of how the comparison is made. Choose a tool of measurement ( 1 m ruler, watch, balance, …) • Count how many standard units that match the physical quantity you want to measure (2 m, 10 sec, 5 kg, …) • Record the result. The result consists of numerical number and a unit Example: length of pencil is 12 cm, weight of apple is 30 gram

Example • Follow the four steps to measure the length of a line (shown as red). Use a ruler as a tool • Standard or unit= cm, measurement tool= ruler Caution: all measurements include 1. number, and 2. unit A measurement without a unit is meaningless. Can you say that the length of this bridge is 3 ? ? ?

Measurement systems SI system: a modified metric system Table (1. 1) Measurements in Metric and SI systems Measurement Metric (symbol) SI (symbol) Length Meter(m) Mass Gram (g) Kilogram (kg) Volume Liter (L) Cubic meter(m 3) Time Seconds (sec) Temperature Celsius ( 0 C) Kelvin (K) Uses prefixes or powers of 10

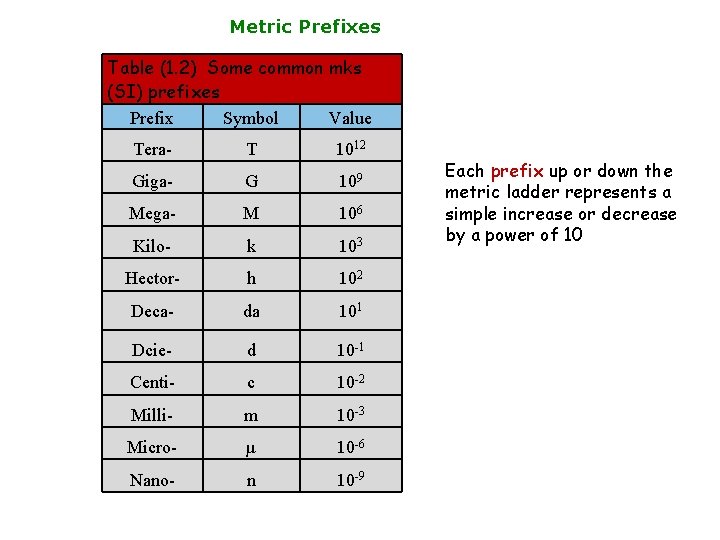
Metric Prefixes Table (1. 2) Some common mks (SI) prefixes Prefix Symbol Value Tera- T 1012 Giga- G 109 Mega- M 106 Kilo- k 103 Hector- h 102 Deca- da 101 Dcie- d 10 -1 Centi- c 10 -2 Milli- m 10 -3 Micro- µ 10 -6 Nano- n 10 -9 Each prefix up or down the metric ladder represents a simple increase or decrease by a power of 10

Example Use Table (1. 1) and indicate whether the unit of each of the following measurements describes, length, mass, or volume, and others • A 10 kg basket of apples. ------- • Ahmad is 1. 70 m tall. -------- • A medication shot contains 10 g insulin. ------- • A bottle of milk contains 1. 5 L of milk. ------- • The air inside the room is set at 25 0 C. -------

Example Use Table (1. 2) and identify the measurement that has an SI unit. • Salem’s height is • 1. 75 yd (B) 5. 8 ft (C) 1. 75 m (D) 0. 5 km • The temperature at PL 1 lab is • 75 0 C (B) 345 K (C) 160 0 F (D) 230 in • The mass of an orange is • 59 lb (B) 65 L (D) 0. 123 kg (C) 34 oz

Scientific Notation To write large and small numbers in powers of 10 If the number is greater than 1 If the number is less than 1 • Move the decimal point to the left after the first digit to give a number between 1 and 9. • Move the decimal point to the right after the first digital point to give a number between 1 and 9. • The spaces moved are shown as a power of ten. • The power is positive • For example: 34 0000 = • The spaces moved are shown as a power of ten. • The power is negative • For example: 0. 00378 =

Examples (1) Write the number 723 00004 in a scientific notation (2) Write the number 0. 0000521 in a scientific notation

Speed •

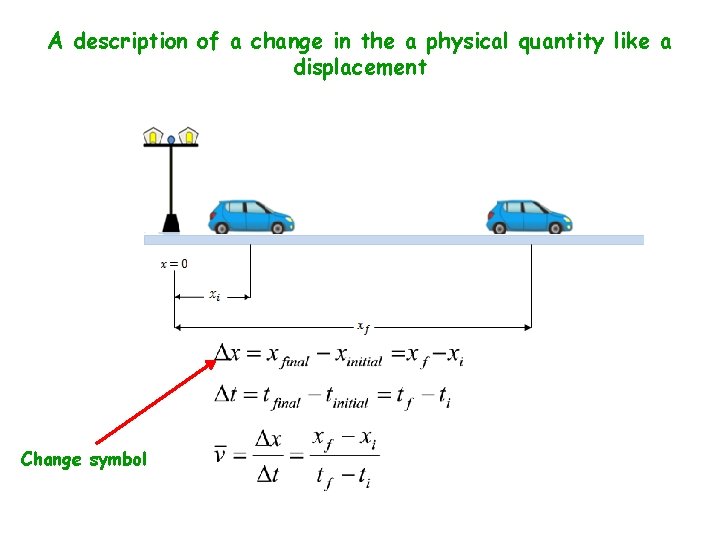
A description of a change in the a physical quantity like a displacement Change symbol

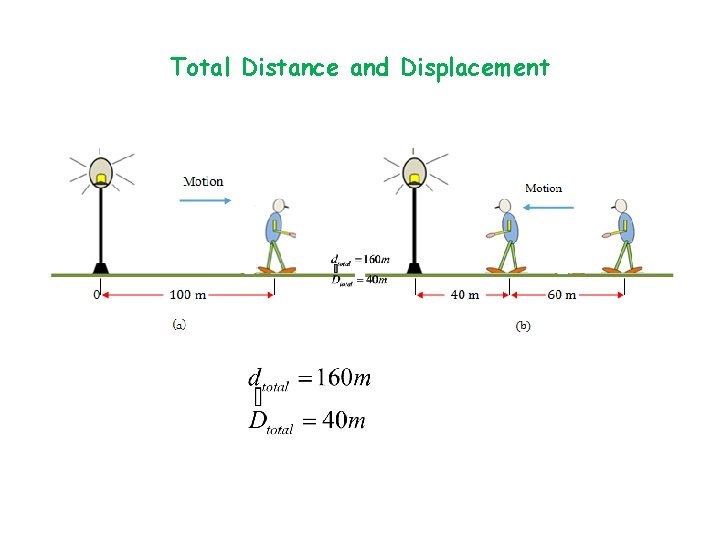
Total Distance and Displacement

Example •

Velocity •

Example • A man starts moving from home (origin (0)) and walks 6 m east (to the right), stopped and found that he forgot his lunch at home. Therefore, he rushed backward (west) heading home. If the total time of his walk both ways is 2 min then find (a) his average speed and (b) his average velocity. Solution

Problems Solving Method The procedure can be outlined as follows: • Read the problem carefully. Read it at least twice • Make a sketch of the problem if it is necessary. Represent any object by a dot or a small box • In your notebook, write down all given information (data) with units. Look at some terms that carry some information. For example, motion from rest means initial velocity equals zero. Also, the term ‘smooth surface’ indicates no friction • Write down the unknown wanted quantity or quantities the question ask for • Think about the right equation that relates all the known and the unknown quantities • Write down the right equation for the unknown quantity • Substitute the data in the right equation, including the units. Verify your answer to see if it does make sense

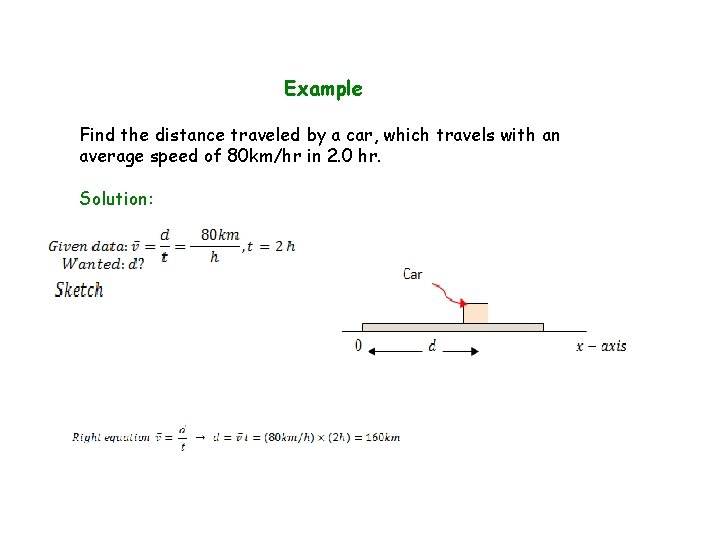
Example Find the distance traveled by a car, which travels with an average speed of 80 km/hr in 2. 0 hr. Solution:

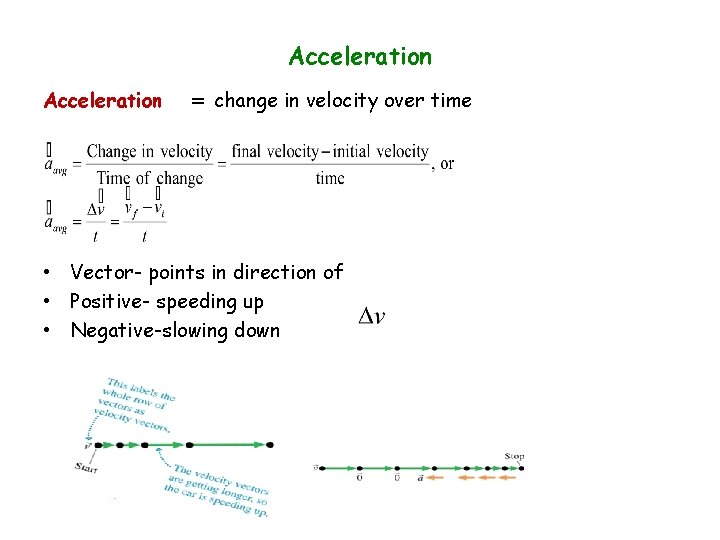
Acceleration = change in velocity over time • Vector- points in direction of • Positive- speeding up • Negative-slowing down

Example A car starts from rest (velocity = 0 m/s) and speeds up to 20 m/s in 10 s. Find its acceleration. Solution: