Motion and Velocity Displacement in Time and Space

Motion and Velocity Displacement in Time and Space

Vectors Graphically Describe DIRECTION and MAGNITUDE One Foot/sec + One Foot/sec = 3 Feet/sec west And You can Add and subtract Them!

Scaling Vectors 6 MPH 6 Inches 6 Centimeters A Vector Describing a Velocity of 6 MPH is Drawn With a Length of 6 Units The Length of a Vector is Proportional to It’s Magnitude

Parallel Vectors Point A 10 miles East Point B 17 miles West The magnitude of the Resultant Vector is found 10 -17=-7 miles east or 7 miles west Total Displacement -7 miles East of the Starting Position

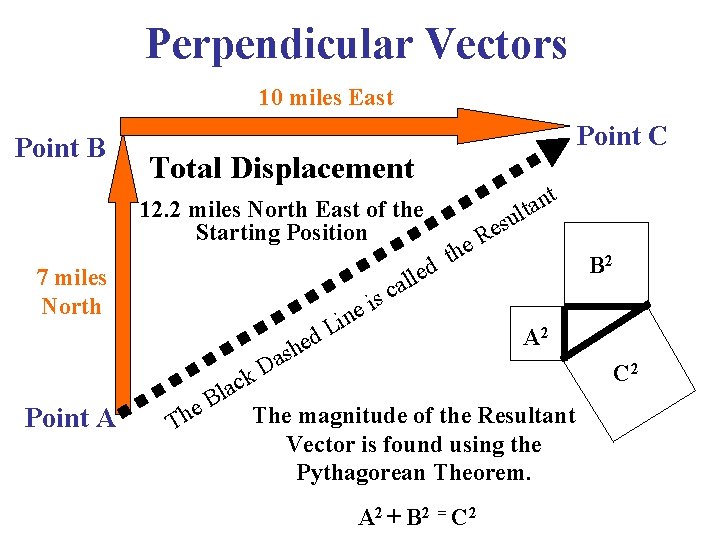
Perpendicular Vectors 10 miles East Point B Total Displacement 12. 2 miles North East of the Starting Position led 7 miles North d e h as Point A Point C Th l B e e n i L al c is su e R e th D k c a t n a lt B 2 A 2 C 2 The magnitude of the Resultant Vector is found using the Pythagorean Theorem. A 2 + B 2 = C 2

Motion or Movement is a Change In Position Called Displacement • As the car moves so does the time. Speed is the Rate of Displacement

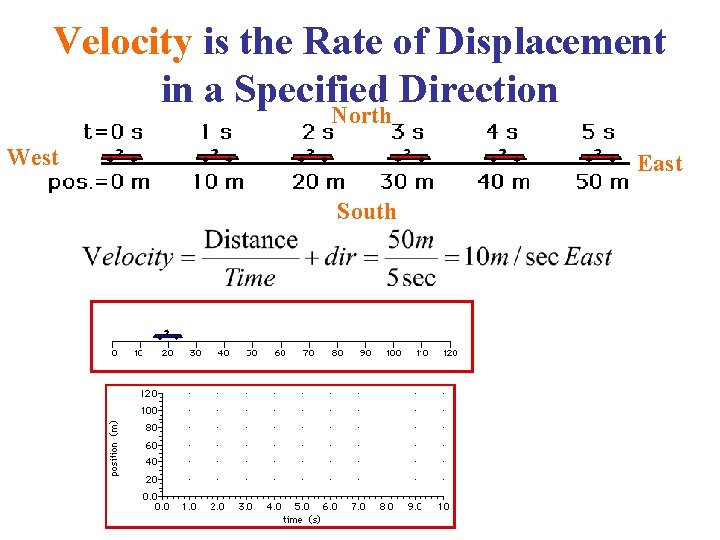
Velocity is the Rate of Displacement in a Specified Direction North West East South

Another Difference Between Speed and Velocity Scalar Quantities time Distance Speed (MPH) Speed is a Scalar Quantity 50 m/s Vector Quantities Force Velocity (Speed and Direction) Acceleration Velocity is a Vector Quantity 50 m/s west

Solving Velocity Problems 1 A car travels 100 meters in 30 seconds west what is the velocity of the car. • Rearranging variables to find what you need. • Solve the problem

Solving Velocity Problems 2 A car travels 20 m/s west how far does it travel in 10 seconds. • Rearranging variables to find what you need. • Solve the problem

Solving Velocity Problems 3 A car travels 20 m/s west for 100 m how long is the car travelling? • Rearranging variables to find what you need. • Solve the problem

Solving Average Velocity • First add up all the distances • Next add up all the times. • Finally, Do the velocity calculation. A man walked 10 m in 2 seconds then 15 m in 3 seconds what is the man’s average velocity? Sum distance=10+15=25 m Sum time=2+3=5 s Average Velocity=25/5=5 m/s

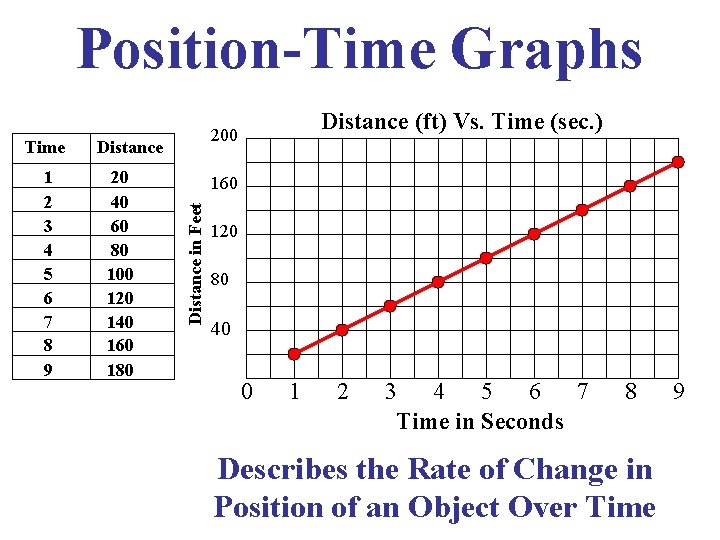
Position-Time Graphs 1 2 3 4 5 6 7 8 9 Distance 20 40 60 80 100 120 140 160 180 160 Distance in Feet Time Distance (ft) Vs. Time (sec. ) 200 120 80 40 0 1 2 3 4 5 6 7 Time in Seconds 8 Describes the Rate of Change in Position of an Object Over Time 9

Graphing Velocity

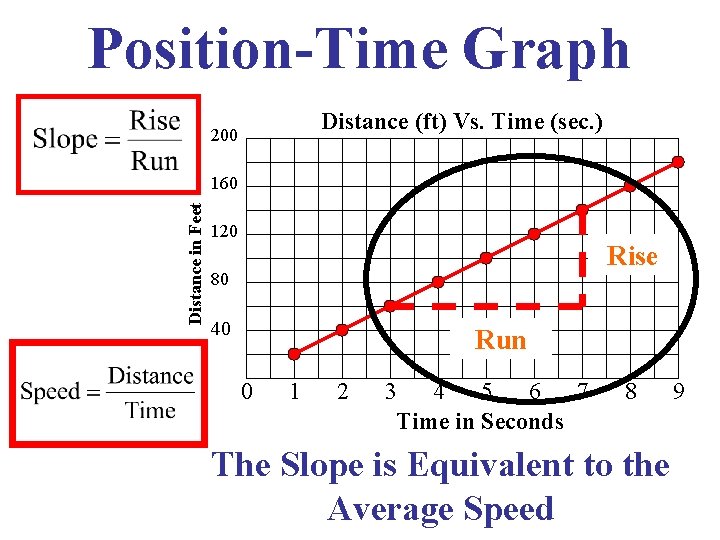
Position-Time Graph Distance (ft) Vs. Time (sec. ) 200 Distance in Feet 160 120 Rise 80 40 Run 0 1 2 3 4 5 6 7 Time in Seconds 8 The Slope is Equivalent to the Average Speed 9

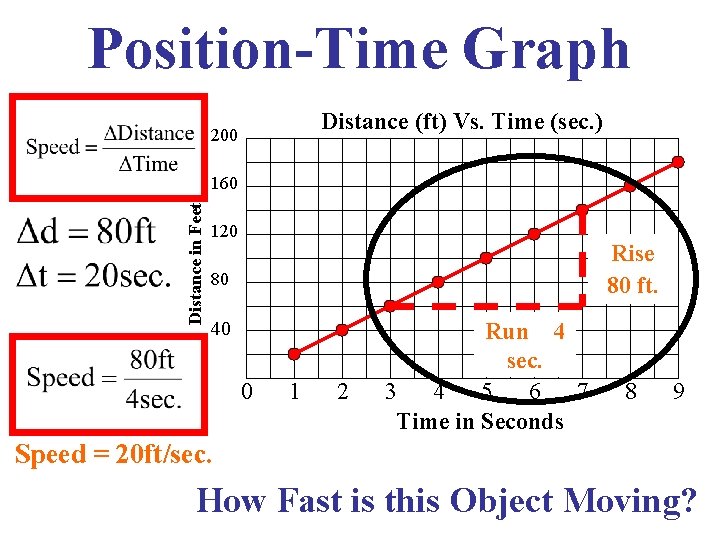
Position-Time Graph Distance (ft) Vs. Time (sec. ) 200 Distance in Feet 160 120 Rise 80 ft. 80 40 0 1 2 Run 4 sec. 3 4 5 6 7 Time in Seconds 8 9 Speed = 20 ft/sec. How Fast is this Object Moving?

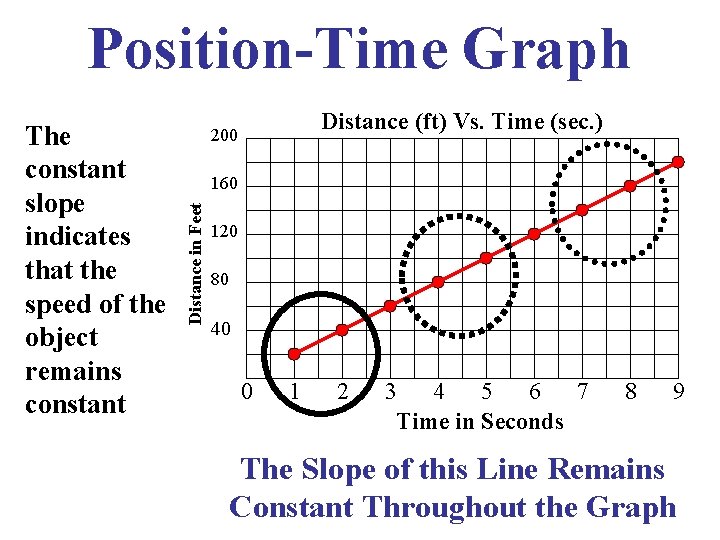
Position-Time Graph 160 Distance in Feet The constant slope indicates that the speed of the object remains constant Distance (ft) Vs. Time (sec. ) 200 120 80 40 0 1 2 3 4 5 6 7 Time in Seconds 8 9 The Slope of this Line Remains Constant Throughout the Graph

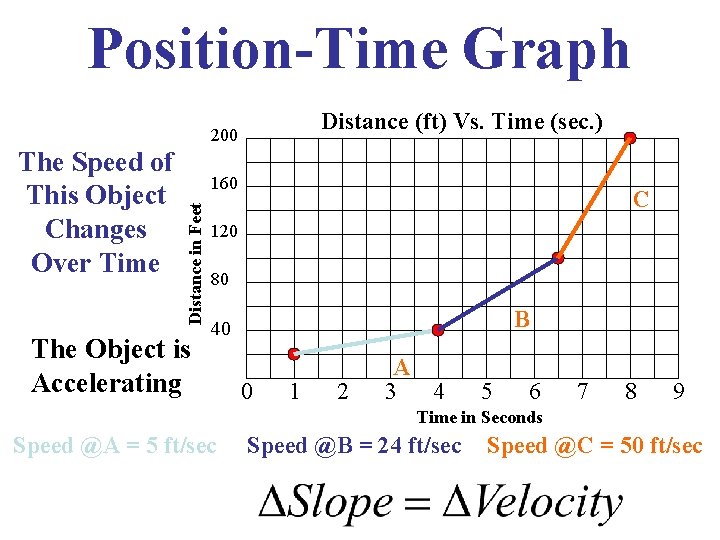
Position-Time Graph Distance (ft) Vs. Time (sec. ) 200 160 Distance in Feet The Speed of This Object Changes Over Time The Object is Accelerating C 120 80 B 40 0 1 2 A 3 4 5 6 7 8 9 Time in Seconds Speed @A = 5 ft/sec Speed @B = 24 ft/sec Speed @C = 50 ft/sec