Most Important Element in life Most important Element

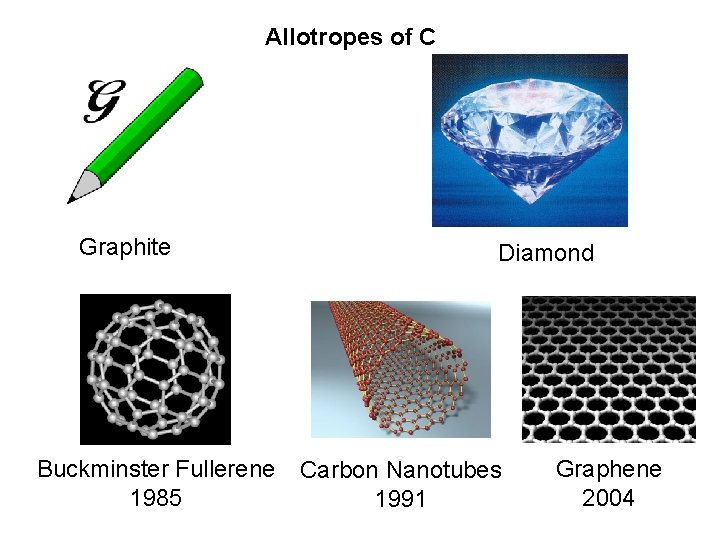
Most Important Element in life Most important Element in Engineering Most important element in Nanotechnology C

Allotropes of C Graphite Buckminster Fullerene 1985 Diamond Carbon Nanotubes 1991 Graphene 2004

Contents Crystal, Lattice and Motif Unit cells, Lattice Parameters and Projections Classification of Lattices: 7 crystal systems 14 Bravais lattices Miller Indices & Miller-Bravais Indices Directions and Planes Reciprocal lattice

Crystal, Lattice and Motif Crystal ? A 3 D translationaly periodic arrangement of atoms in space is called a crystal.

Crystal, Lattice and Motif Lattice? A 3 D translationally periodic arrangement of points in space is called a lattice.

Crystal, Lattice and Motif Crystal Lattice A 3 D translationally periodic arrangement of atoms A 3 D translationally periodic arrangement of points

Crystal, Lattice and Motif? Crystal = Lattice + Motif or basis: an atom or a group of atoms associated with each lattice point

“Nothing that is worth knowing can be taught. ” Oscar Wilde

Lattice + Motif = Crystal + Love Lattice Love Pattern + = Heart = (Motif) Love Pattern (Crystal)

Maurits Cornelis Escher 1898 -1972 Dutch Graphic Artist Air, Water and Earth

Every periodic pattern (and hence a crystal) has a unique lattice associated with it

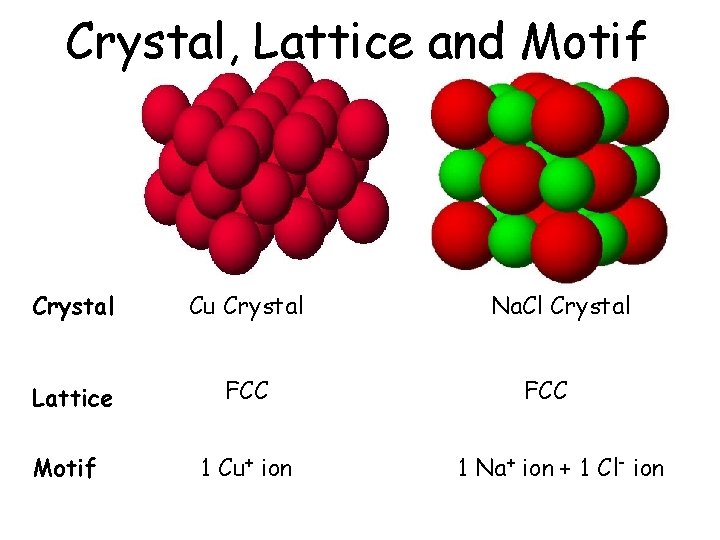
Crystal, Lattice and Motif Crystal Cu Crystal Lattice FCC Motif 1 Cu+ ion Na. Cl Crystal FCC 1 Na+ ion + 1 Cl- ion

Contents Crystal, Lattice and Motif Unit cells, Lattice Parameters and Projections Classification of Lattices: 7 crystal systems 14 Bravais lattices Miller Indices & Miller-Bravais Indices Directions and Planes

Unit cell description : 1 Translational Periodicity One can select a small volume of the crystal which by periodic repetition generates the entire crystal (without overlaps or gaps) Unit Cell

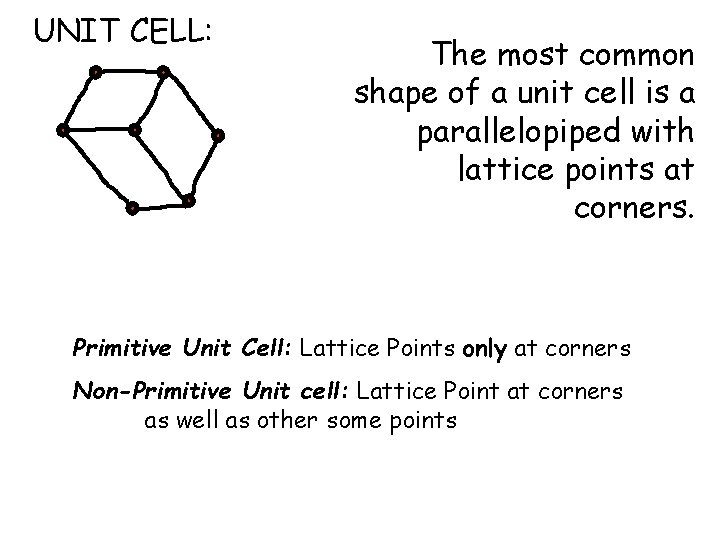
UNIT CELL: The most common shape of a unit cell is a parallelopiped with lattice points at corners. Primitive Unit Cell: Lattice Points only at corners Non-Primitive Unit cell: Lattice Point at corners as well as other some points

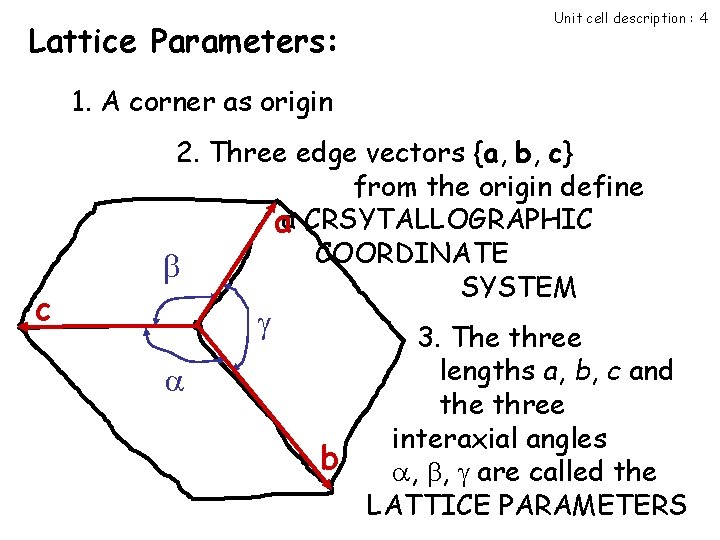
Lattice Parameters: Unit cell description : 4 1. A corner as origin c 2. Three edge vectors {a, b, c} from the origin define aa CRSYTALLOGRAPHIC COORDINATE SYSTEM b 3. The three lengths a, b, c and the three interaxial angles , , are called the LATTICE PARAMETERS

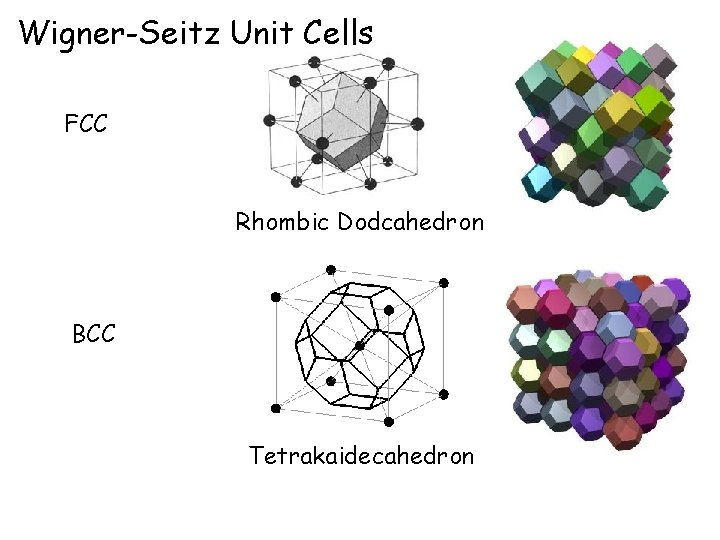
Wigner-Seitz Unit Cells FCC Rhombic Dodcahedron BCC Tetrakaidecahedron

The six lattice parameters a, b, c, , , The cell of the lattice + Motif crystal

Contents Crystal, Lattice and Motif Unit cells, Lattice Parameters and Projections Classification of Lattices: 7 crystal systems 14 Bravais lattices Miller Indices & Miller-Bravais Indices Directions and Planes

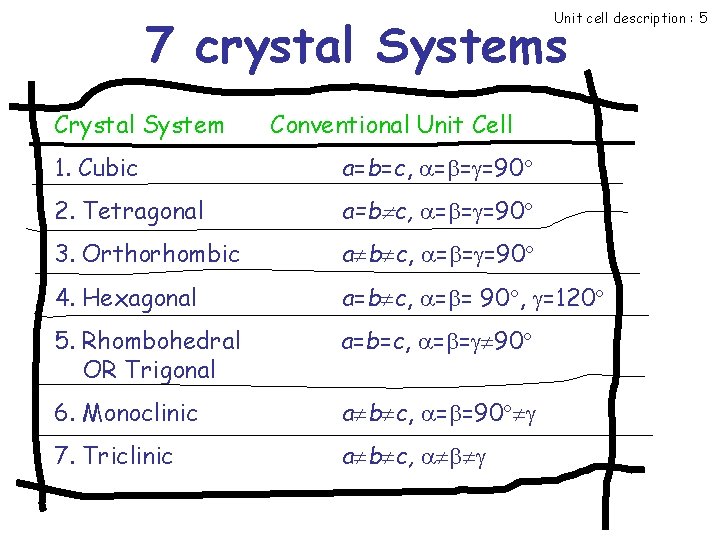
Unit cell description : 5 7 crystal Systems Crystal System Conventional Unit Cell 1. Cubic a=b=c, = = =90 2. Tetragonal a=b c, = = =90 3. Orthorhombic a b c, = = =90 4. Hexagonal a=b c, = = 90 , =120 5. Rhombohedral OR Trigonal a=b=c, = = 90 6. Monoclinic a b c, = =90 7. Triclinic a b c,

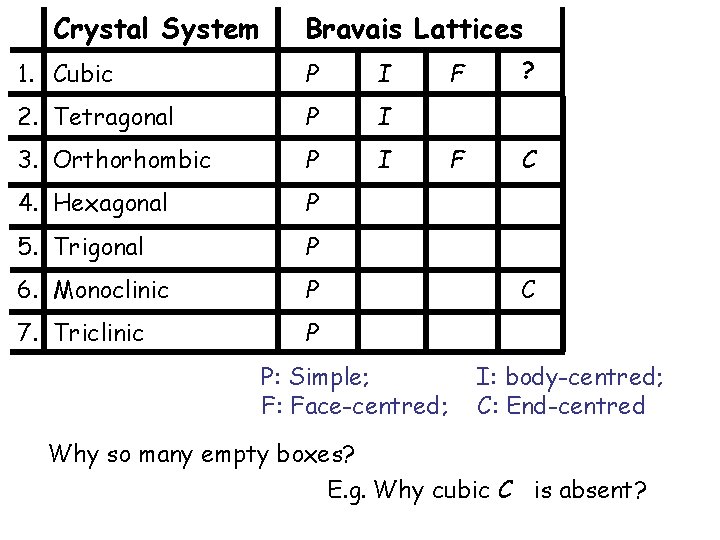
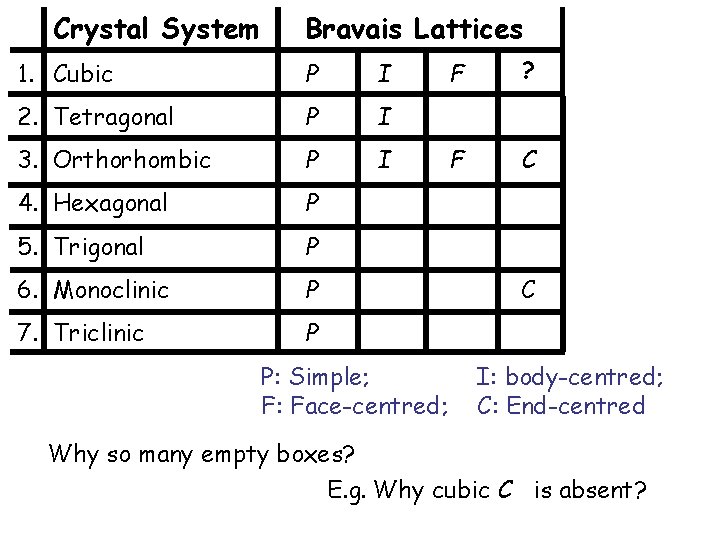
Crystal System Bravais Lattices 1. Cubic P I 2. Tetragonal P I 3. Orthorhombic P I 4. Hexagonal P 5. Trigonal P 6. Monoclinic P 7. Triclinic P P: Simple; F: Face-centred; F ? F C C I: body-centred; C: End-centred Why so many empty boxes? E. g. Why cubic C is absent?

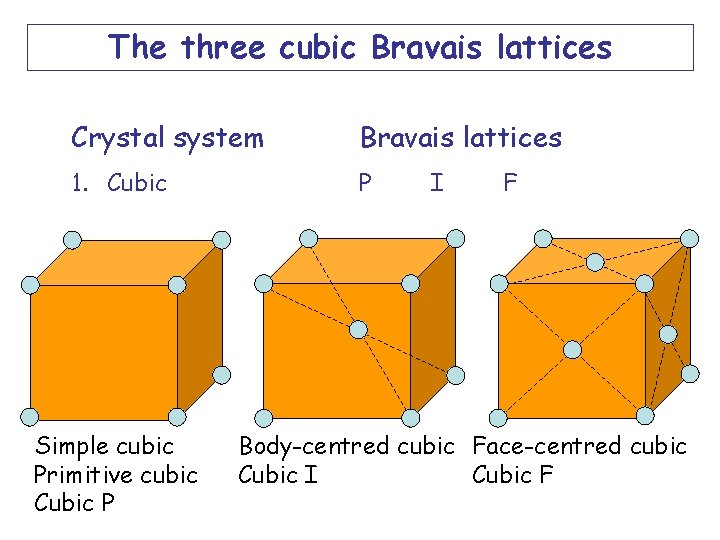
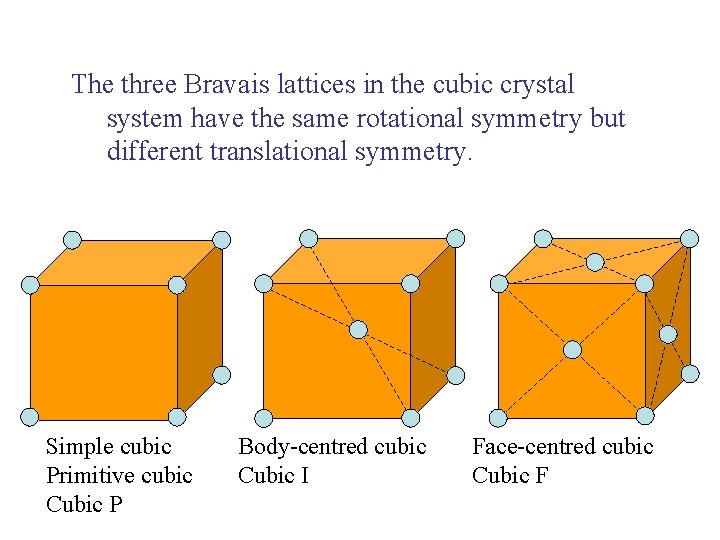
The three cubic Bravais lattices Crystal system Bravais lattices 1. Cubic P Simple cubic Primitive cubic Cubic P I F Body-centred cubic Face-centred cubic Cubic I Cubic F

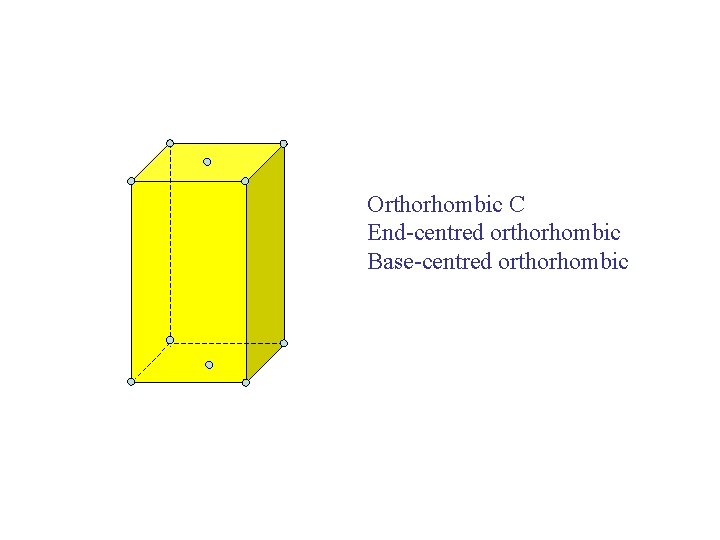
Orthorhombic C End-centred orthorhombic Base-centred orthorhombic

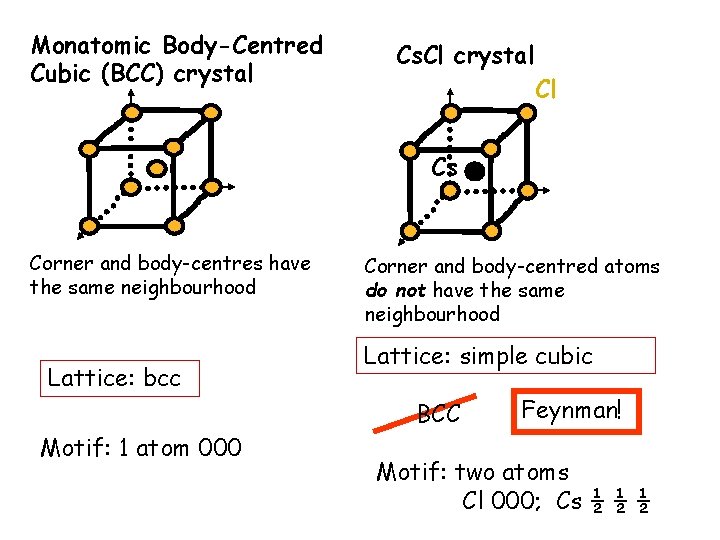
Monatomic Body-Centred Cubic (BCC) crystal Cs. Cl crystal Cl Cs Corner and body-centres have the same neighbourhood Lattice: bcc Corner and body-centred atoms do not have the same neighbourhood Lattice: simple cubic BCC Motif: 1 atom 000 Feynman! Motif: two atoms Cl 000; Cs ½ ½ ½

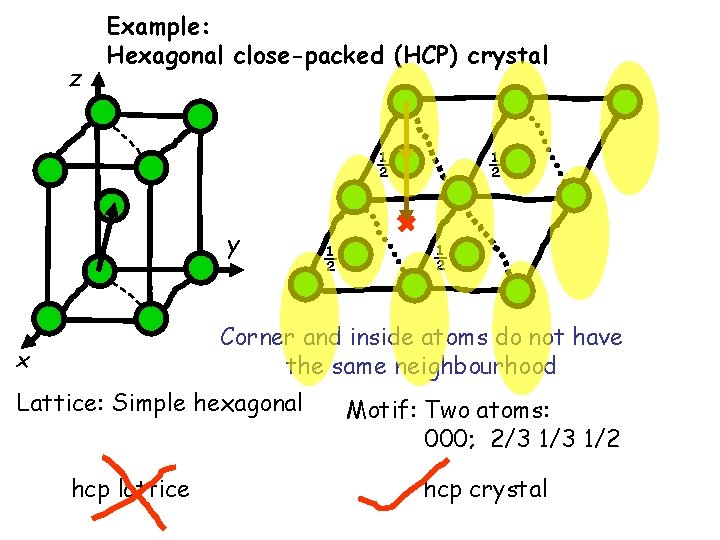
z Example: Hexagonal close-packed (HCP) crystal ½ y ½ ½ ½ Corner and inside atoms do not have the same neighbourhood x Lattice: Simple hexagonal hcp lattice Motif: Two atoms: 000; 2/3 1/2 hcp crystal

Crystal System Bravais Lattices 1. Cubic P I 2. Tetragonal P I 3. Orthorhombic P I 4. Hexagonal P 5. Trigonal P 6. Monoclinic P 7. Triclinic P P: Simple; F: Face-centred; F ? F C C I: body-centred; C: End-centred Why so many empty boxes? E. g. Why cubic C is absent?

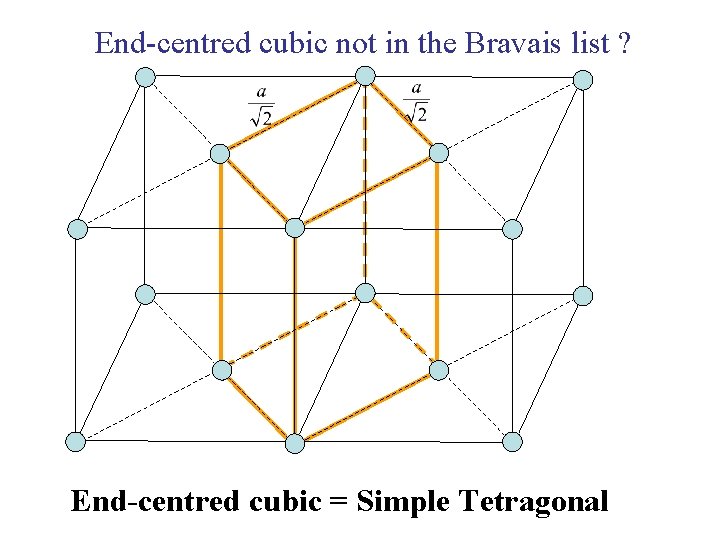
End-centred cubic not in the Bravais list ? End-centred cubic = Simple Tetragonal

14 Bravais lattices divided into seven crystal systems Crystal system Bravais lattices 1. Cubic P I 2. Tetragonal P I 3. Orthorhombic P I 4. Hexagonal P 5. Trigonal P 6. Monoclinic P 7. Triclinic P F C C

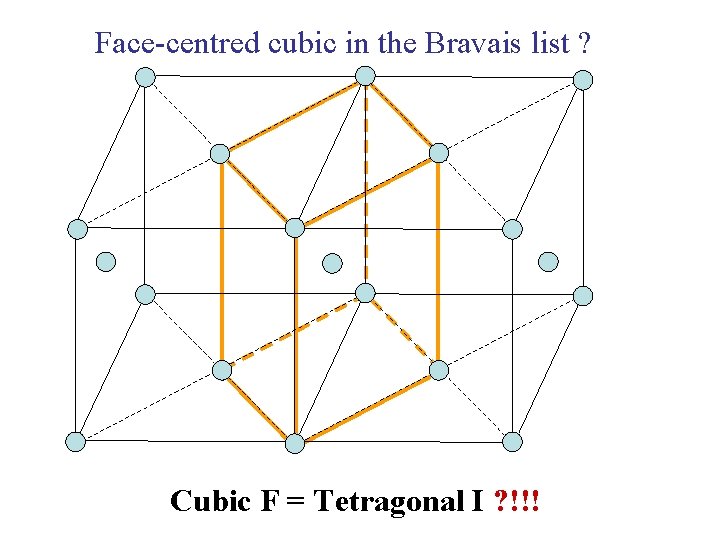
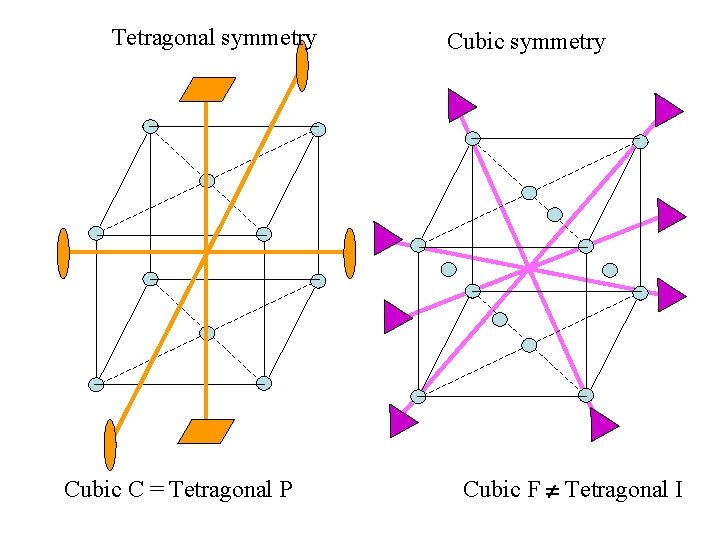
Face-centred cubic in the Bravais list ? Cubic F = Tetragonal I ? !!!

14 Bravais lattices divided into seven crystal systems Crystal system Bravais lattices 1. Cubic P I 2. Tetragonal P I 3. Orthorhombic P I 4. Hexagonal P 5. Trigonal P 6. Monoclinic P 7. Triclinic P F C C

History: ML Frankenheim 1801 -1869 1835: 15 X lattices 1856: 14 lattices Couldn’t find his photo on the net Auguste Bravais AML 750 1811 -1863 IIT-D 1850: 14 lattices 06 Aug 2009: 13 lattices !!!

Why can’t the Face. Centred Cubic lattice (Cubic F) be considered as a Body-Centred Tetragonal lattice (Tetragonal I) ?

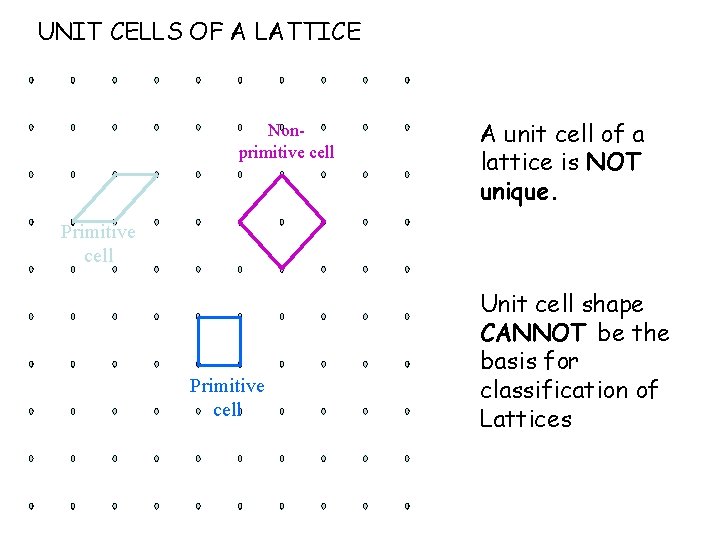
UNIT CELLS OF A LATTICE Nonprimitive cell A unit cell of a lattice is NOT unique. Primitive cell Unit cell shape CANNOT be the basis for classification of Lattices

What is the basis for classification of lattices into 7 crystal systems and 14 Bravais lattices?

Lattices are classified on the basis of their symmetry

What is symmetry?

Symmetry If an object is brought into selfcoincidence after some operation it said to possess symmetry with respect to that operation.

NOW NO SWIMS ON MON

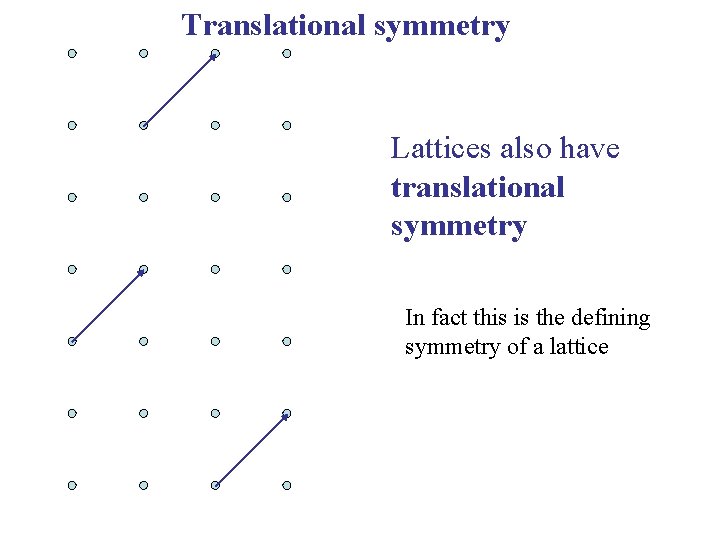
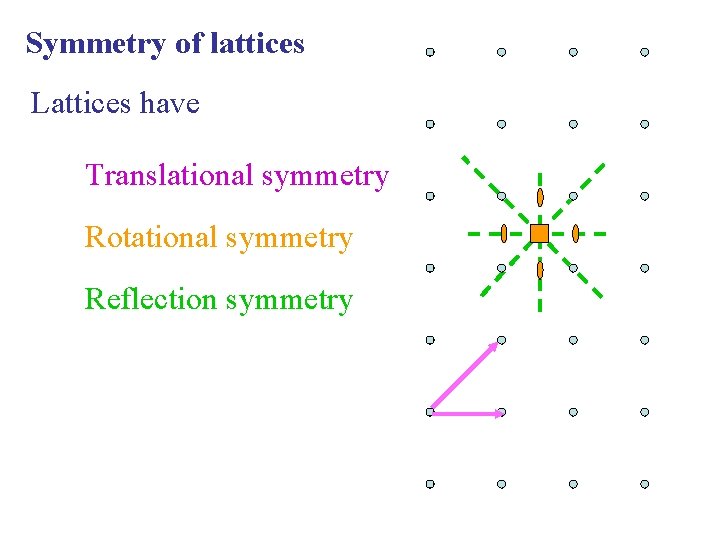
Translational symmetry Lattices also have translational symmetry In fact this is the defining symmetry of a lattice

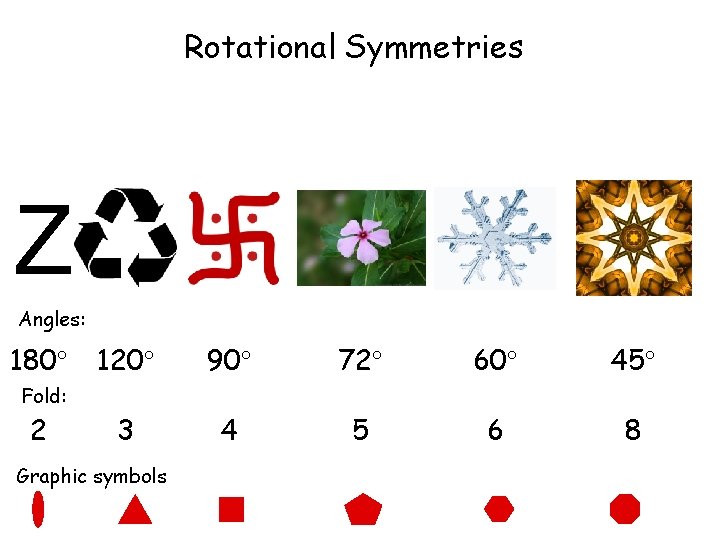
Rotation Axis If an object come into self-coincidence through smallest non-zero rotation angle of then it is said to have an nfold rotation axis where =180 n=2 2 -fold rotation axis =90 n=4 4 -fold rotation axis

Rotational Symmetries Z Angles: 180 120 90 72 60 45 3 4 5 6 8 Fold: 2 Graphic symbols

Crsytallographic Restriction 5 -fold symmetry or Pentagonal symmetry is not possible for Periodic Tilings Symmetries higher than 6 -fold also not possible Only possible rotational symmetries for periodic tilings 2 3 4 5 6 7 8 9…

Proof of The Crystallographic Restriction A rotation can be represented by a matrix If T is a rotational symmetry of a lattice then all its elements must be integers (wrt primitive basis vectors) N nfold -1 0 180° 120° 2 3 1 90° 4 2 60° 6 3 0° 1

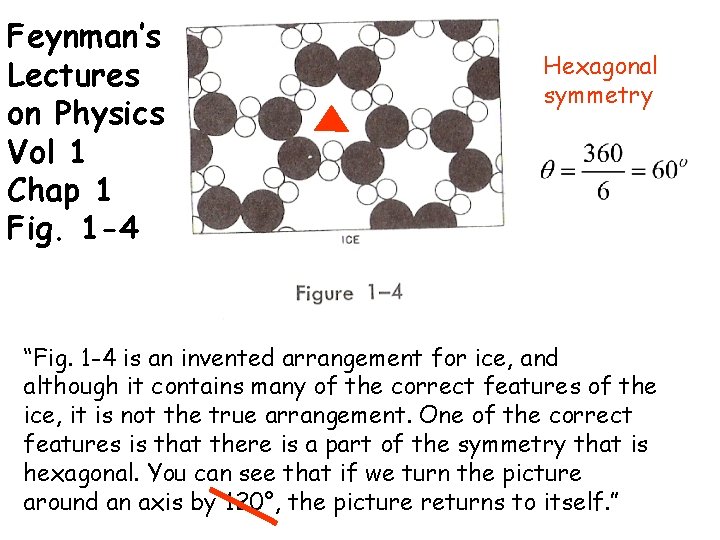
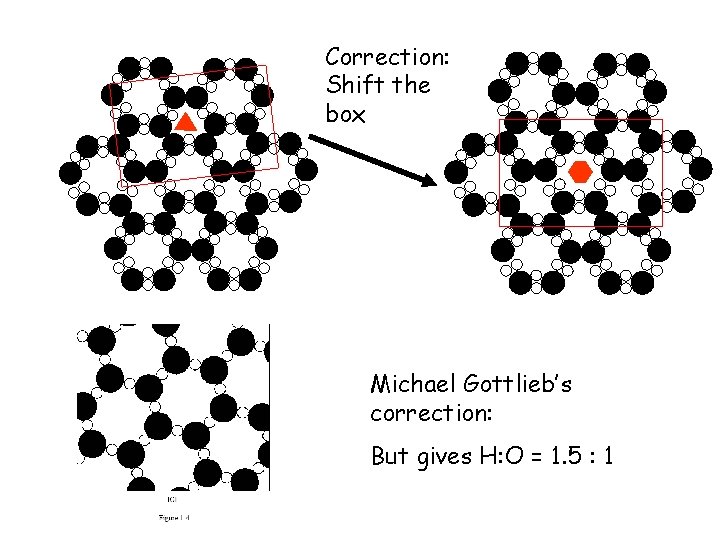
Feynman’s Lectures on Physics Vol 1 Chap 1 Fig. 1 -4 Hexagonal symmetry “Fig. 1 -4 is an invented arrangement for ice, and although it contains many of the correct features of the ice, it is not the true arrangement. One of the correct features is that there is a part of the symmetry that is hexagonal. You can see that if we turn the picture around an axis by 120°, the picture returns to itself. ”

Correction: Shift the box Michael Gottlieb’s correction: But gives H: O = 1. 5 : 1

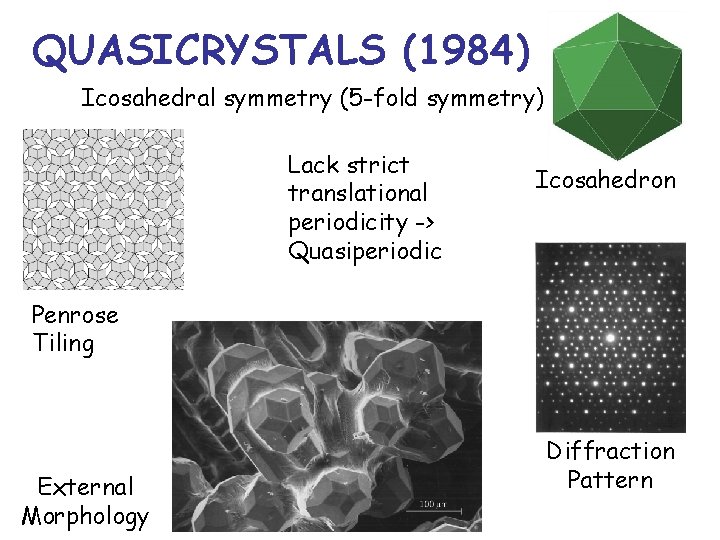
QUASICRYSTALS (1984) Icosahedral symmetry (5 -fold symmetry) Lack strict translational periodicity -> Quasiperiodic Icosahedron Penrose Tiling External Morphology Diffraction Pattern

Reflection (or mirror symmetry)

Symmetry of lattices Lattices have Translational symmetry Rotational symmetry Reflection symmetry

Point Group and Space Group The group of all symmetry elements of a crystal except translations (e. g. rotation, reflection etc. ) is called its POINT GROUP. The complete group of all symmetry elements including translations of a crystal is called its SPACE GROUP

Classification of Lattices Crystal systems and Bravais Lattices Classification of lattices Based on the point group symmetry alone (i. e. excluding translational symmetry 7 types of lattices 7 crystal systems Based on the space group symmetry, i. e. , rotational, reflection and translational symmetry 14 types of lattices 14 Bravais lattices

System 7 crystal Systems Required symmetry • Cubic Three 4 -fold axis • Tetragonal one 4 -fold axis • Orthorhombic three 2 -fold axis • Hexagonal one 6 -fold axis • Rhombohedral one 3 -fold axis • Monoclinic one 2 -fold axis • Triclinic none

Tetragonal symmetry Cubic C = Tetragonal P Cubic symmetry Cubic F Tetragonal I

The three Bravais lattices in the cubic crystal system have the same rotational symmetry but different translational symmetry. Simple cubic Primitive cubic Cubic P Body-centred cubic Cubic I Face-centred cubic Cubic F

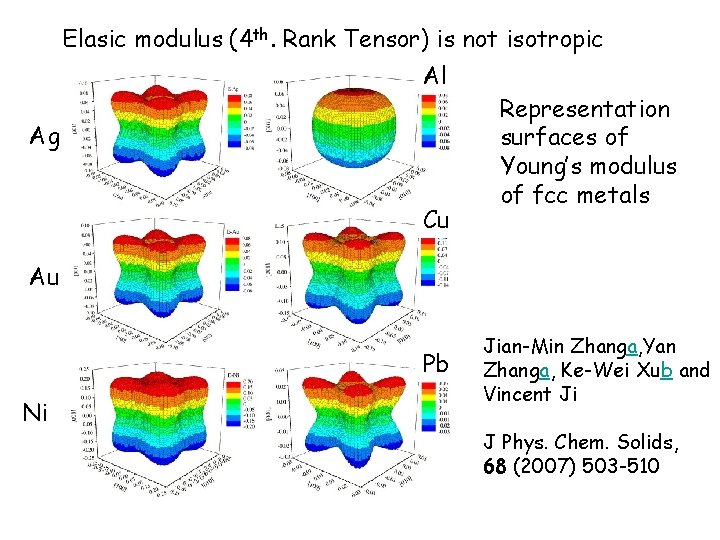
Neumann’s Principle Symmetry elements of a physical property of a crystal must include all the symmetry elements of its point group (i. e. , all its rotational axes and mirror planes). Electrical resistance of a cubic crystal is isotropic (spherical symmetry) All properties that can be represented by tensors of rank up to 2 are isotropic for cubic crystals

Elasic modulus (4 th. Rank Tensor) is not isotropic Al Ag Cu Representation surfaces of Young’s modulus of fcc metals Au Pb Ni Jian-Min Zhanga, Yan Zhanga, Ke-Wei Xub and Vincent Ji J Phys. Chem. Solids, 68 (2007) 503 -510

QUESTIONS?

Contents Crystal, Lattice and Motif Unit cells, Lattice Parameters and Projections Classification of Lattices: 7 crystal systems 14 Bravais lattices Miller Indices & Miller-Bravais Indices Directions and Planes

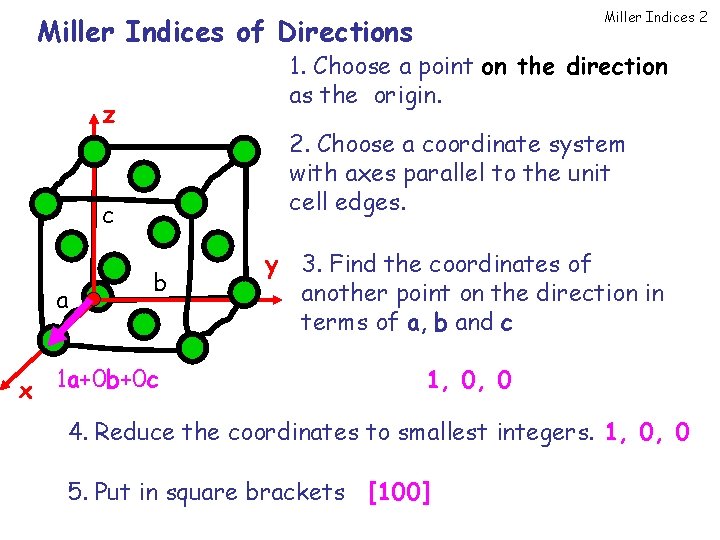
Miller Indices 2 Miller Indices of Directions 1. Choose a point on the direction as the origin. z 2. Choose a coordinate system with axes parallel to the unit cell edges. c a b x 1 a+0 b+0 c y 3. Find the coordinates of another point on the direction in terms of a, b and c 1, 0, 0 4. Reduce the coordinates to smallest integers. 1, 0, 0 5. Put in square brackets [100]

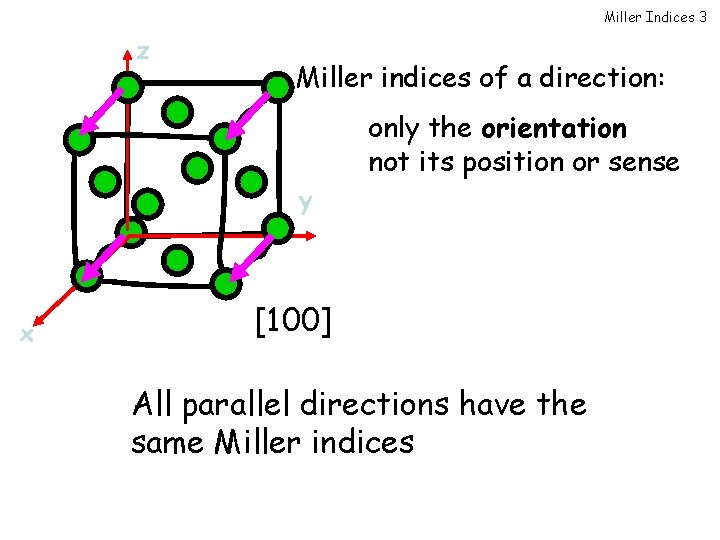
Miller Indices 3 z Miller indices of a direction: only the orientation not its position or sense y x [100] All parallel directions have the same Miller indices

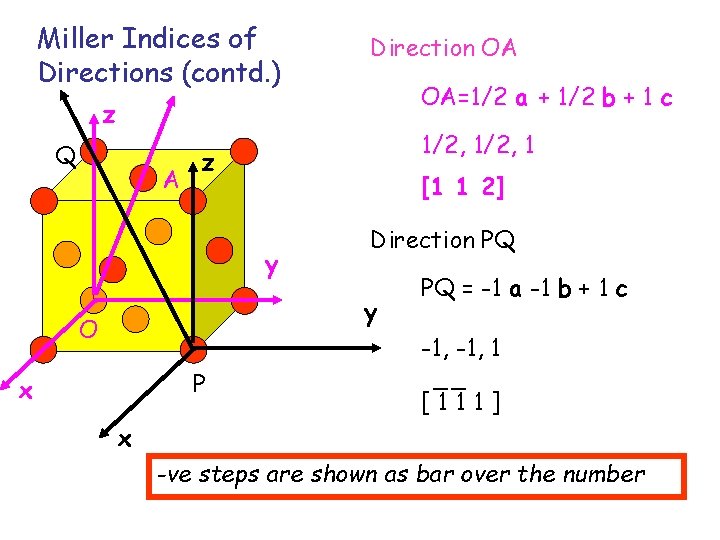
Miller Indices of Directions (contd. ) Direction OA OA=1/2 a + 1/2 b + 1 c z Q A 1/2, 1 z [1 1 2] y Direction PQ y O P x PQ = -1 a -1 b + 1 c -1, 1 __ [111] x -ve steps are shown as bar over the number

Miller Indices 4 Miller indices of a family of symmetry related directions = [uvw] and all other directions related to [uvw] by the symmetry of the crystal [001] Tetragonal Cubic [010] [100] = [100], [010], [001] [100] = [100], [010]

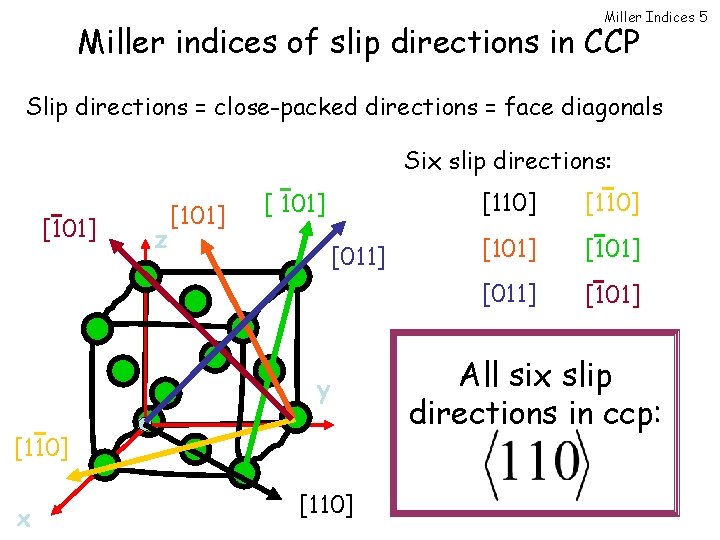
Miller Indices 5 Miller indices of slip directions in CCP Slip directions = close-packed directions = face diagonals Six slip directions: [101] z [101] [011] y [110] x [110] [101] [011] [101] All six slip directions in ccp:

Vectors vs Directions: Miller Indices of a direction [110] is a direction along the face diagonal of a unit cell. It is not a vector of fixed length Exception: The Burger’s vector BCC FCC A vector equal to half body diagonal A vector equal to half face diagonal

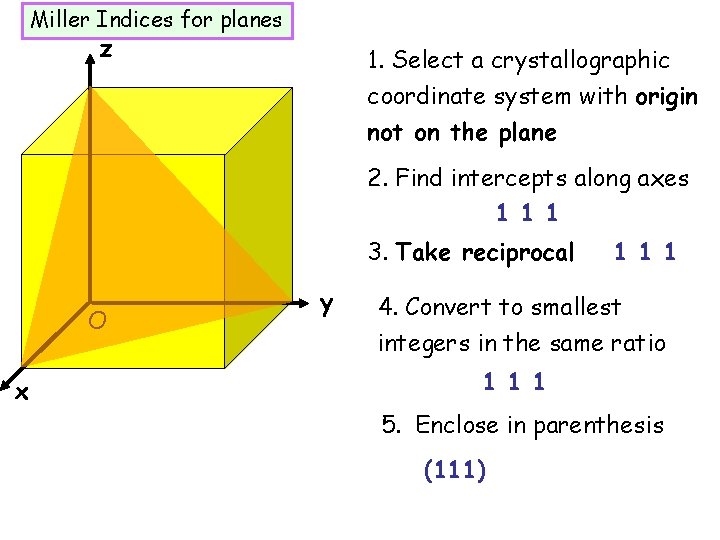
Miller Indices for planes z 1. Select a crystallographic coordinate system with origin not on the plane 2. Find intercepts along axes 1 1 1 3. Take reciprocal O x y 1 1 1 4. Convert to smallest integers in the same ratio 1 1 1 5. Enclose in parenthesis (111)

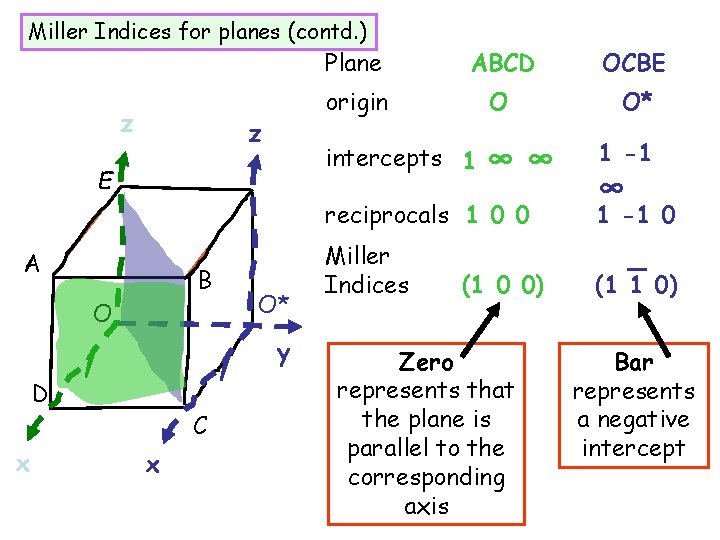
Miller Indices for planes (contd. ) z z E Plane ABCD OCBE origin O O* intercepts 1 ∞ ∞ reciprocals 1 0 0 A B O O* y D x C x Miller Indices (1 0 0) Zero represents that the plane is parallel to the corresponding axis 1 -1 ∞ 1 -1 0 _ (1 1 0) Bar represents a negative intercept

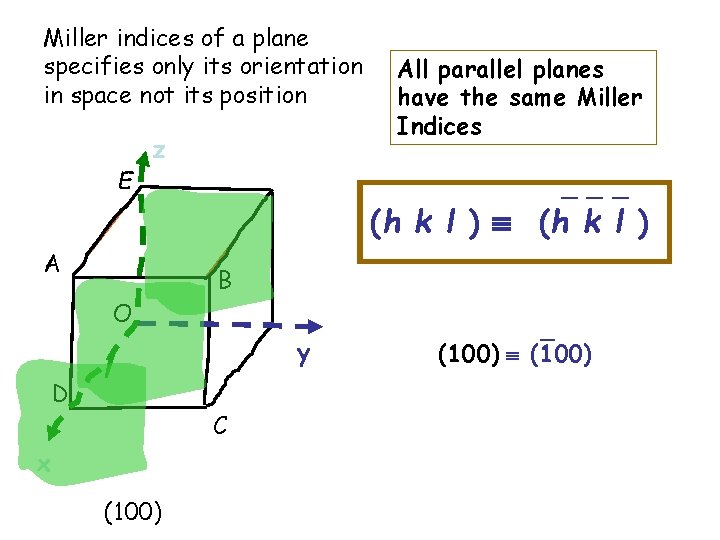
Miller indices of a plane specifies only its orientation in space not its position E z All parallel planes have the same Miller Indices _ _ _ (h k l ) A B O y D C x (100) _ (100)

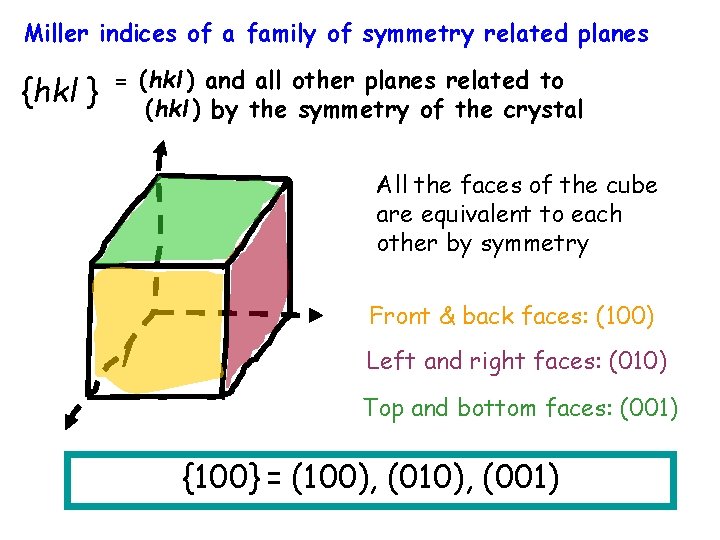
Miller indices of a family of symmetry related planes {hkl } = (hkl ) and all other planes related to (hkl ) by the symmetry of the crystal All the faces of the cube are equivalent to each other by symmetry Front & back faces: (100) Left and right faces: (010) Top and bottom faces: (001) {100} = (100), (010), (001)

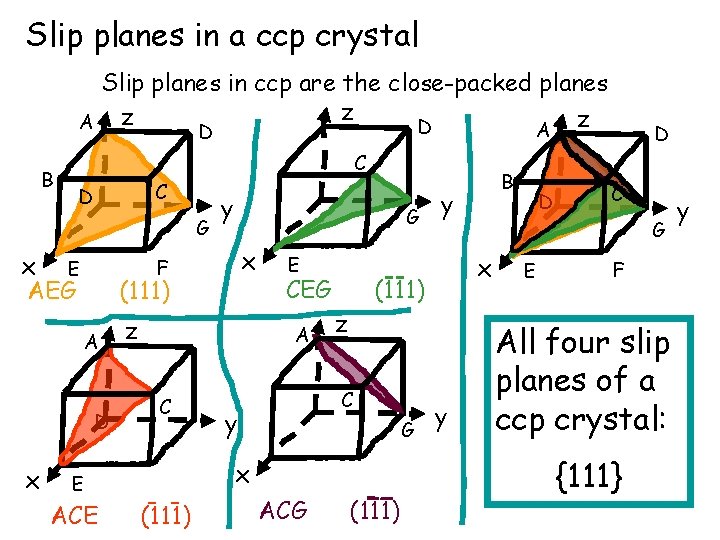
Slip planes in a ccp crystal Slip planes in ccp are the close-packed planes z A z D B C C D G x E AEG y x (111) D x y G F A z CEG z C y G (111) ACG (111) y D C G x (111) x E ACE E A C B D E F All four slip planes of a ccp crystal: {111} y

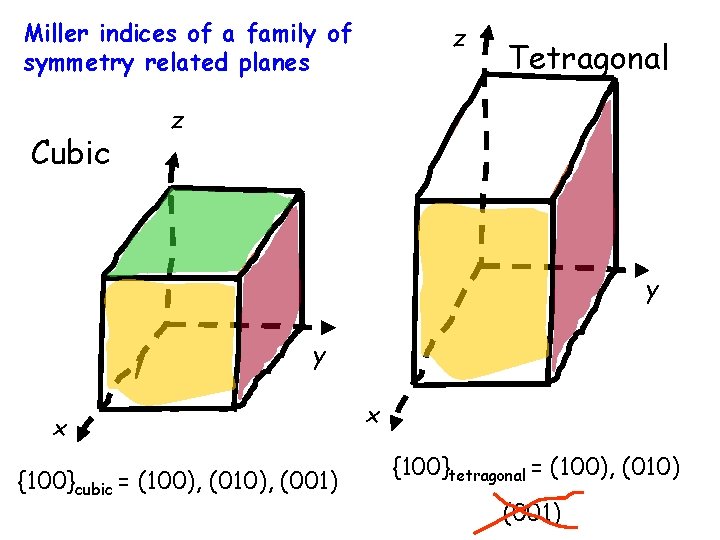
Miller indices of a family of symmetry related planes Cubic z Tetragonal z y y x {100}cubic = (100), (010), (001) x {100}tetragonal = (100), (010) (001)

Symmetry related directions in the hexagonal crystal system z = [100], [010], [110] Not permutations = [100], [010], [001] [110] [010] x [100] y Permutations

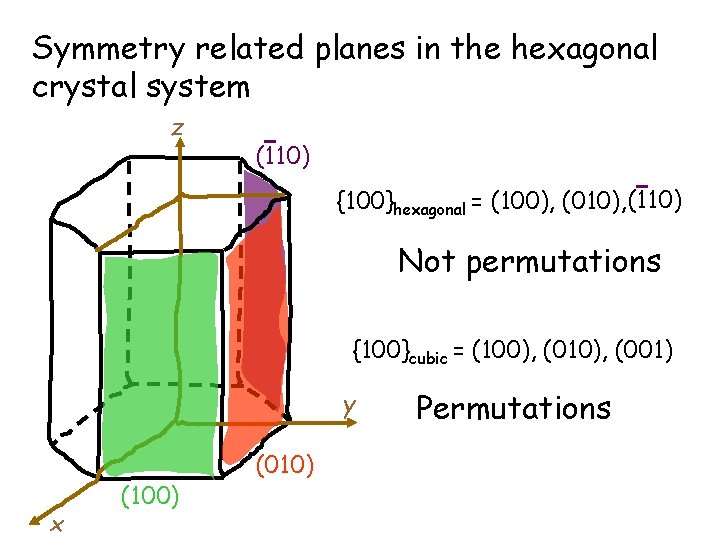
Symmetry related planes in the hexagonal crystal system z (110) {100}hexagonal = (100), (010), (110) Not permutations {100}cubic = (100), (010), (001) y x (100) (010) Permutations

Problem: In hexagonal system symmetry related planes and directions do NOT have Miller indices which are permutations Solution: Use the four-index Miller. Bravais Indices instead

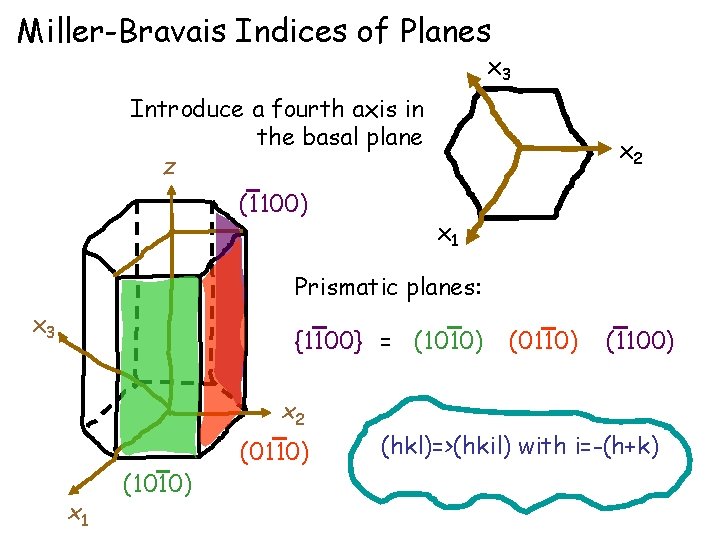
Miller-Bravais Indices of Planes x 3 Introduce a fourth axis in the basal plane z (1100) x 2 x 1 Prismatic planes: x 3 {1100} = (1010) x 2 x 1 (1010) (0110) (1100) (hkl)=>(hkil) with i=-(h+k)

Miller-Bravais Indices of Directions in hexagonal crystals [uvw]=>[UVTW] Basal plane =slip plane =(0001) Vectorially Require that: x 3 a 2 x 1 a 2 x 2

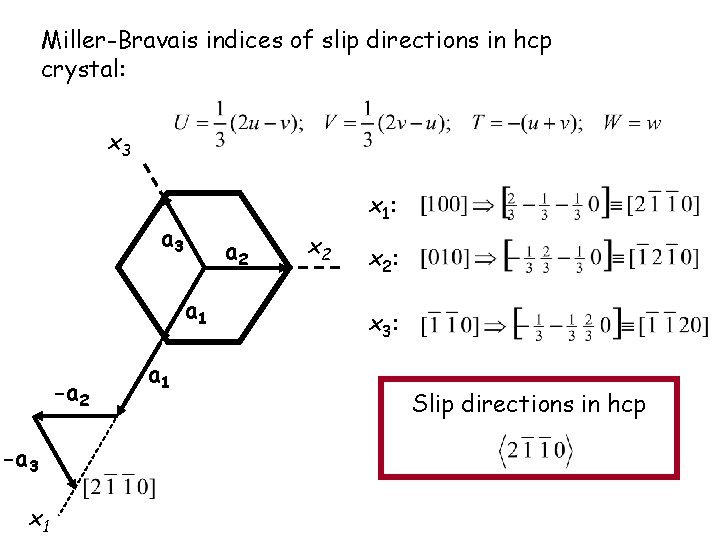
Miller-Bravais indices of slip directions in hcp crystal: x 3 x 1: a 3 a 2 a 1 -a 2 -a 3 x 1 a 1 x 2: x 3: Slip directions in hcp

Some IMPORTANT Results Weiss zone law Condition for a direction [uvw] to be parallel to a plane or lie in the plane (hkl): hu+kv+lw=0 h U + k V + i T +l W = 0 True for ALL crystal systems

CUBIC CRYSTALS [111] [hkl] (hkl) (111) Angle between two directions [h 1 k 1 l 1] and [h 2 k 2 l 2]: C

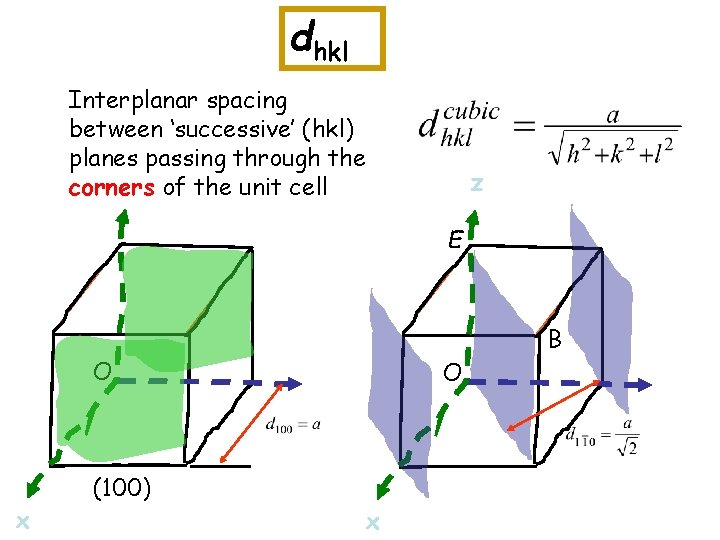
dhkl Interplanar spacing between ‘successive’ (hkl) planes passing through the corners of the unit cell z E B O x (100) O x

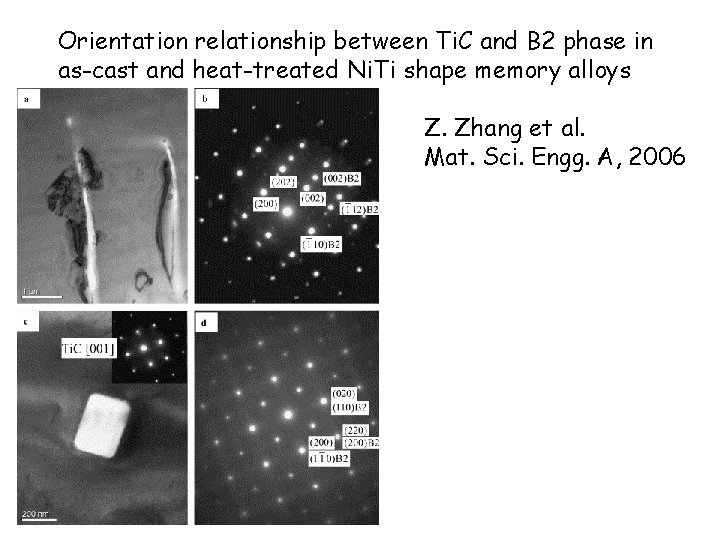
Orientation Relationships In solid state phase-transformation, the new crystalline phase has a particular orientation relationship with the parent phase. When proeutectioid ferrite forms from austenite in steels the following orientation relationship, known as Kurdjumov-Sachs relationship is observed:

Orientation relationship between Ti. C and B 2 phase in as-cast and heat-treated Ni. Ti shape memory alloys Z. Zhang et al. Mat. Sci. Engg. A, 2006

Dendrite Growth Directions FCC BCC HCP

Summary of Notation convention for Indices [uvw] Miller indices of a direction (i. e. a set of parallel directions) <uvw> Miller indices of a family of symmetry related directions (hkl) Miller Indices of a plane (i. e. a set of parallel planes) {hkl} Miller indices of a family of symmetry related planes [uvtw] (hkil) Miller-Bravais indices of a direction, plane in a hexagonal system

Thank You