MOSFET IVs ECE 663 Operation of a transistor

MOSFET I-Vs ECE 663

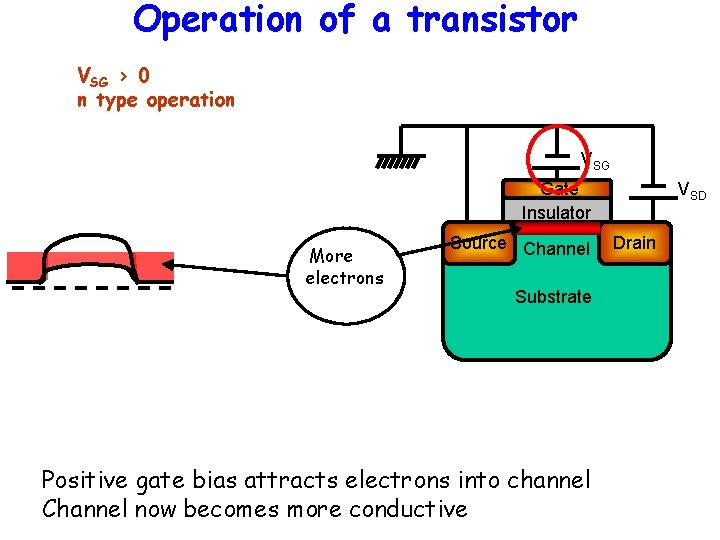
Operation of a transistor VSG > 0 n type operation VSG Gate Insulator More electrons Source Channel Substrate Positive gate bias attracts electrons into channel Channel now becomes more conductive VSD Drain

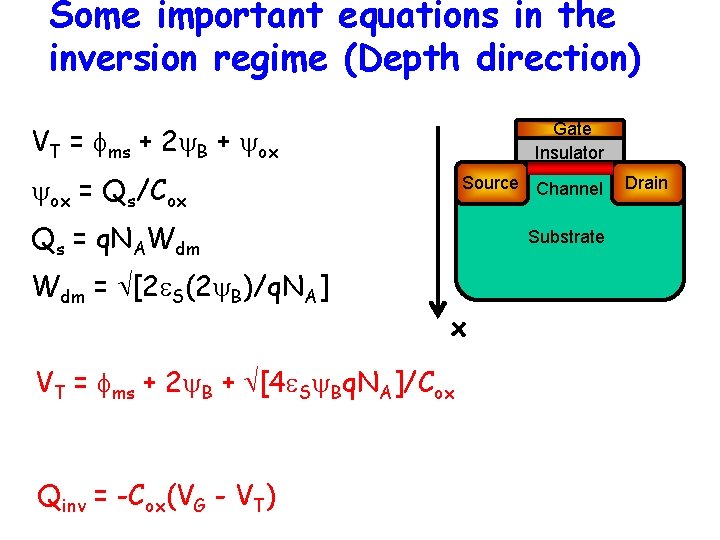
Some important equations in the inversion regime (Depth direction) Gate Insulator VT = fms + 2 B + ox ox = Qs/Cox Source Channel Qs = q. NAWdm = [2 e. S(2 B)/q. NA] Substrate x VT = fms + 2 B + [4 e. S Bq. NA]/Cox Qinv = -Cox(VG - VT) Drain

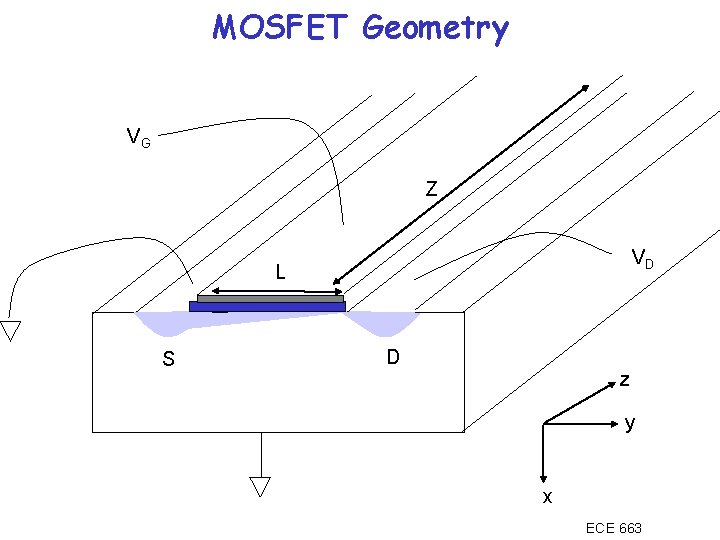
MOSFET Geometry VG Z VD L S D z y x ECE 663

How to include y-dependent potential without doing the whole problem over? ECE 663

Assume potential V(y) varies slowly along channel, so the x-dependent and y-dependent electrostats are independent (GRADUAL CHANNEL APPROXIMATION) i. e. , Ignore ∂Ex/∂y Potential is separable in x and y ECE 663

How to include y-dependent potentials? VG = S + [2 e. S Sq. NA]/Cox S = 2 B + V(y) Need VG – V(y) > VT to invert channel at y (V increases threshold) Since V(y) largest at drain end, that end reverts from inversion to depletion first (Pinch off) SATURATION [VDSAT = VG – VT] ECE 663

So current: j = qninvv = (Qinv/tinv)v I = j. A = j. Ztinv = ZQinvv Qinv = -Cox[VG – VT - V(y)] v = -meffd. V(y)/dy ECE 663

So current: I = meff ZCox[VG – VT - V(y)]d. V(y)/dy Continuity implies ∫Idy = IL I = meff ZCox[(VG – VT )VD- VD 2/2]/L ECE 663

But this current behaves like a parabola !! I = meff ZCox[(VG – VT )VD- VD 2/2]/L ID IDsat VD We have assumed inversion in our model (ie, always above pinch-off) So we just extend the maximum current into saturation… Easy to check that above current is maximum for VDsat = VG - VT Substituting, IDsat = (Coxmeff. Z/2 L)(VG-VT)2 ECE 663

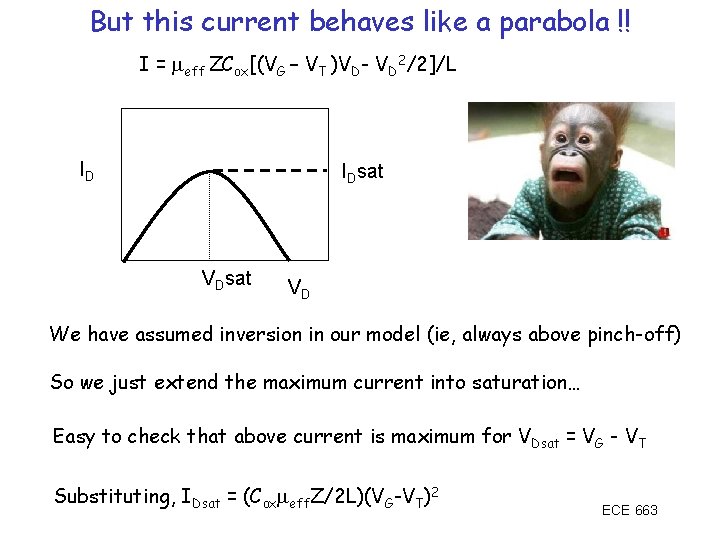
What’s Pinch off? V 0 G VG VG 0 0 0 VD Now add in the drain voltage to drive a current. Initially you get an increasing current with increasing drain bias When you reach VDsat = VG – VT, inversion is disabled at the drain end (pinch-off), but the source end is still inverted The charges still flow, just that you can’t draw more current with higher drain bias, and the current saturates

W NE Square law theory of MOSFETs I = meff ZCox[(VG – VT )VD- VD 2/2]/L, I = meff ZCox(VG – VT )2/2 L, V D > VG - VT J = qnv n ~ Cox(VG – VT ) v ~ meff. VD /L V D < VG - VT

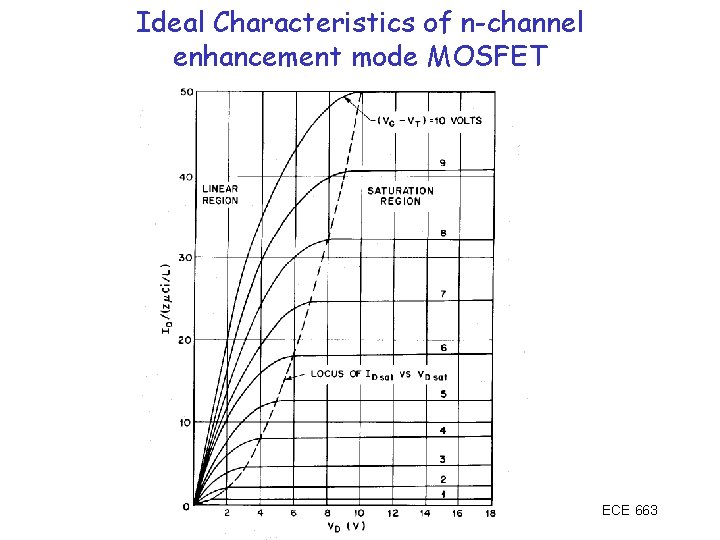
Ideal Characteristics of n-channel enhancement mode MOSFET ECE 663

Drain current for REALLY small VD Linear operation Channel Conductance: Transconductance: ECE 663

In Saturation • Channel Conductance: • Transconductance: ECE 663

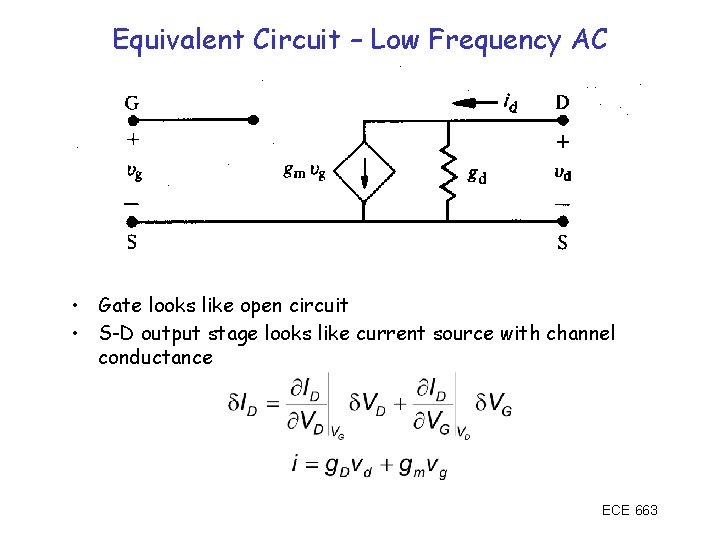
Equivalent Circuit – Low Frequency AC • Gate looks like open circuit • S-D output stage looks like current source with channel conductance ECE 663

Equivalent Circuit – Higher Frequency AC • Input stage looks like capacitances gate-to-source(gate) and gate-to-drain(overlap) • Output capacitances ignored -drain-to-source capacitance small ECE 663

Equivalent Circuit – Higher Frequency AC • Input circuit: • Input capacitance is mainly gate capacitance • Output circuit: ECE 663

Maximum Frequency (not in saturation) • Ci is capacitance per unit area and Cgate is total capacitance of the gate • F=fmax when gain=1 (iout/iin=1) ECE 663

W NE Maximum Frequency (not in saturation) (Inverse transit time) ECE 663

Switching Speed, Power Dissipation ton = Cox. ZLVD/ION Trade-off: If Cox too small, Cs and Cd take over and you lose control of the channel potential (e. g. saturation) (DRAIN-INDUCED BARRIER LOWERING/DIBL) If Cox increases, you want to make sure you don’t control immobile charges (parasitics) which do not contribute to current. ECE 663

Switching Speed, Power Dissipation Pdyn = ½ Cox. ZLVD 2 f Pst = Ioff. VD ECE 663

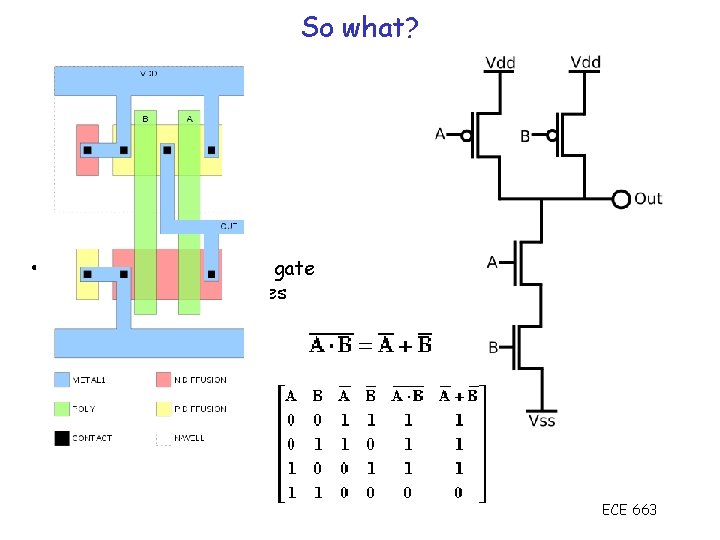
CMOS NOT gate (inverter) ECE 663

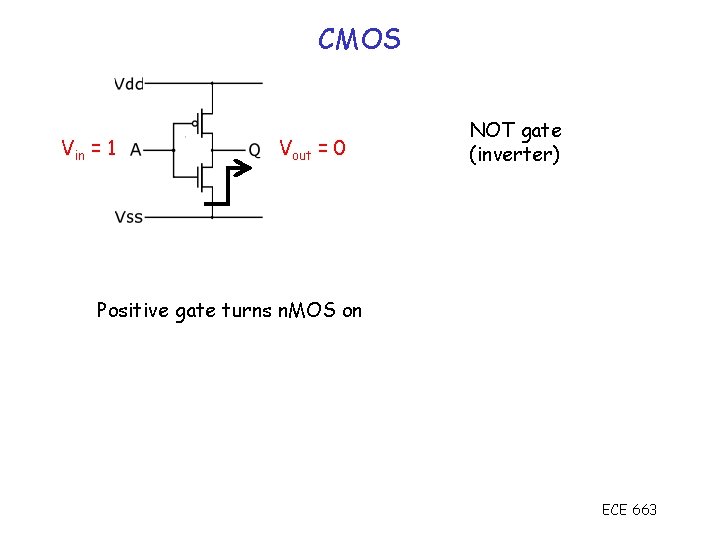
CMOS Vin = 1 Vout = 0 NOT gate (inverter) Positive gate turns n. MOS on ECE 663

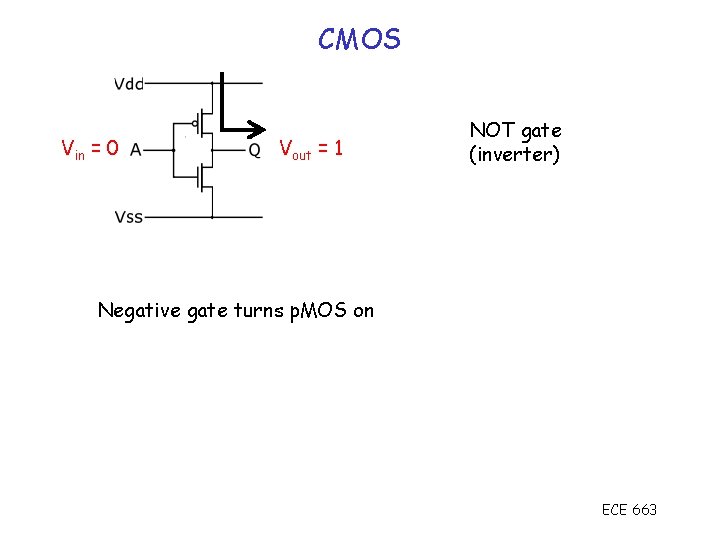
CMOS Vin = 0 Vout = 1 NOT gate (inverter) Negative gate turns p. MOS on ECE 663

So what? • If we can create a NOT gate we can create other gates (e. g. NAND, EXOR) ECE 663

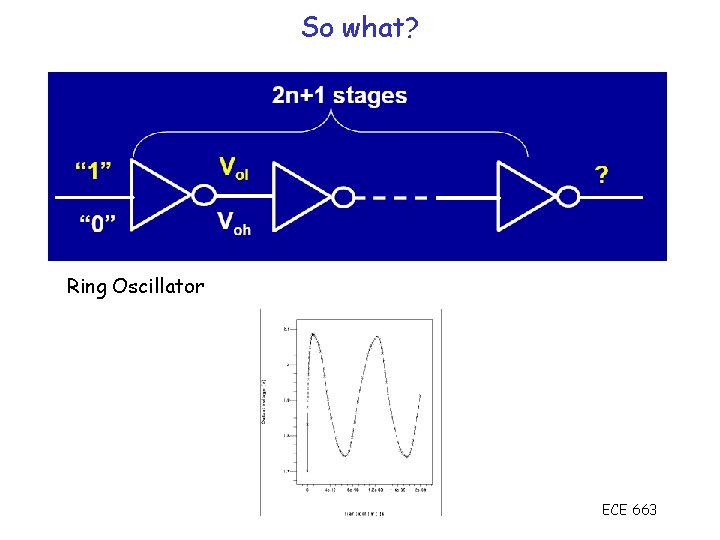
So what? Ring Oscillator ECE 663

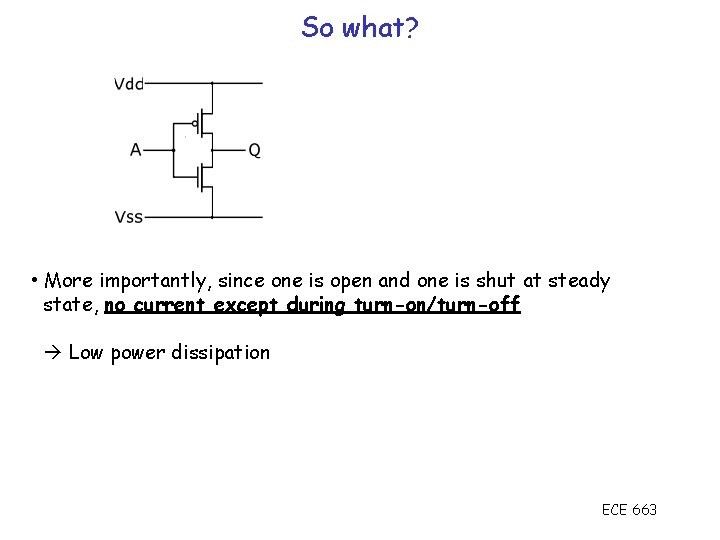
So what? • More importantly, since one is open and one is shut at steady state, no current except during turn-on/turn-off Low power dissipation ECE 663

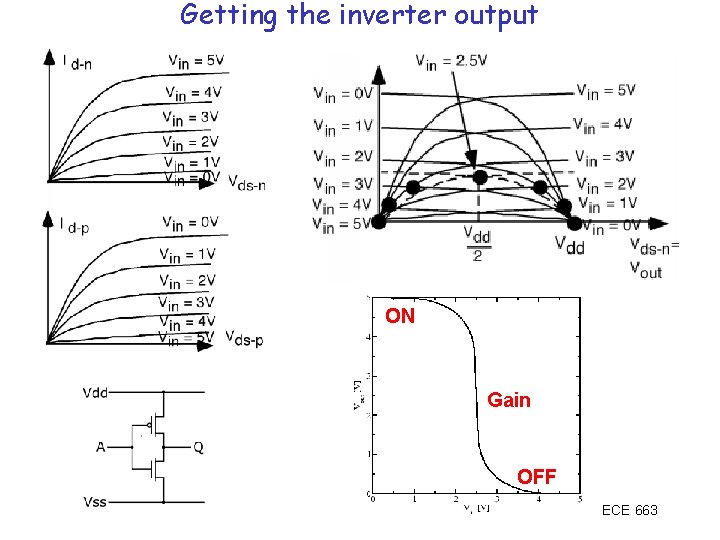
Getting the inverter output ON Gain OFF ECE 663

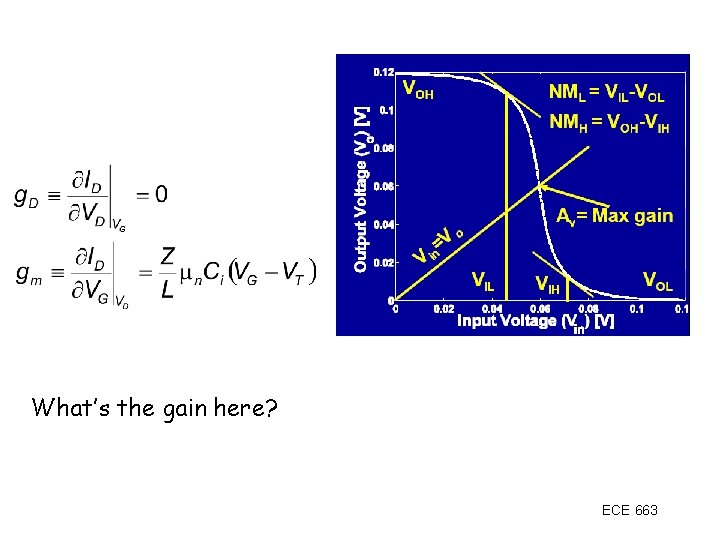
What’s the gain here? ECE 663

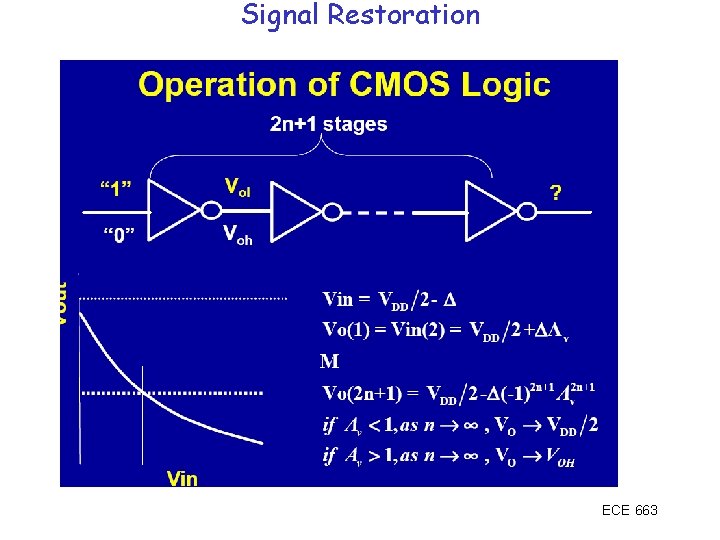
Signal Restoration ECE 663

NEW BJT vs MOSFET • RTL logic vs CMOS logic • DC Input impedance of MOSFET (at gate end) is infinite Thus, current output can drive many inputs FANOUT • CMOS static dissipation is low!! ~ IOFFVDD • Normally BJTs have higher transconductance/current (faster!) IC = (qni 2 Dn/WBND)exp(q. VBE/k. T) gm = IC/ VBE = IC/(k. T/q) ID = m. Cox. W(VG-VT) 2/L gm = ID/ VG = ID/[(VG-VT)/2] • Today’s MOSFET ID >> IC due to near ballistic operation ECE 663

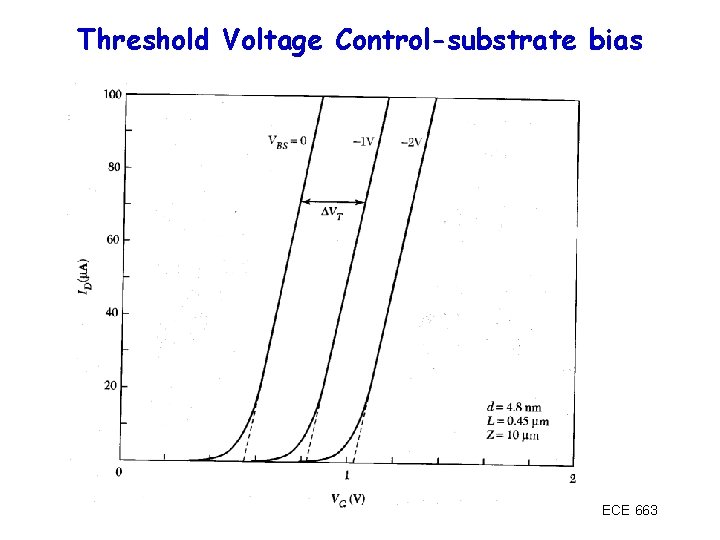
What if it isn’t ideal? • If work function differences and oxide charges are present, threshold voltage is shifted just like for MOS capacitor: • If the substrate is biased wrt the Source (VBS) the threshold voltage is also shifted ECE 663

Threshold Voltage Control • Substrate Bias: ECE 663

Threshold Voltage Control-substrate bias ECE 663

It also affects the I-V VG The threshold voltage is increased due to the depletion region that grows at the drain end because the inversion layer shrinks there and can’t screen it any more. (Wd > Wdm) Qinv = -Cox[VG-VT(y)], I = -meff. ZQinvd. V(y)/dy VT(y) = y + √ 2 esq. NAy/Cox y = 2 y. B + V(y) ECE 663

It also affects the I-V IL = ∫meff. ZCox[VG – (2 y. B+V) - √ 2 esq. NA(2 y. B+V)/Cox]d. V I = (Zmeff. Cox/L)[(VG– 2 y. B)VD –VD 2/2 -2√ 2 esq. NA{(2 y. B+VD)3/2 -(2 y. B)3/2}/3 Cox] ECE 663

We can approximately include this… Include an additional charge term from the depletion layer capacitance controlling V(y) Q = -Cox[VG-VT]+(Cox + Cd)V(y) where Cd = es/Wdm Q = -Cox[VG –VT - MV(y)], M = 1 + Cd/Cox ID = (Zmeff. Cox/L)[(VG-VT - MVD/2)VD] ECE 663

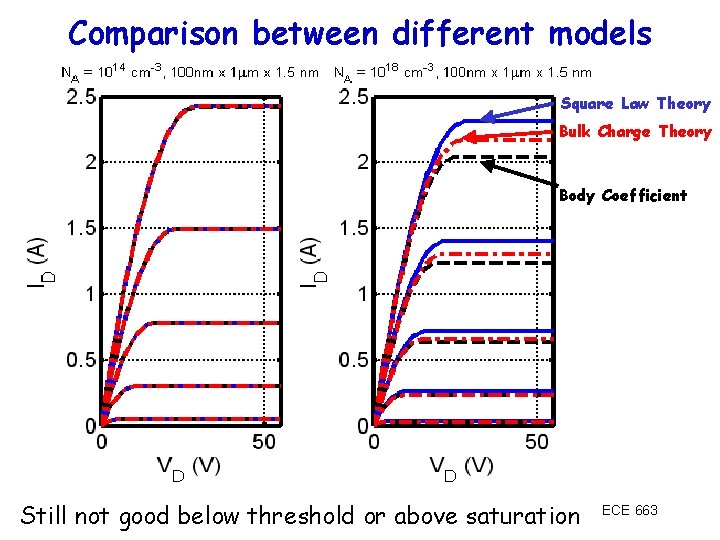
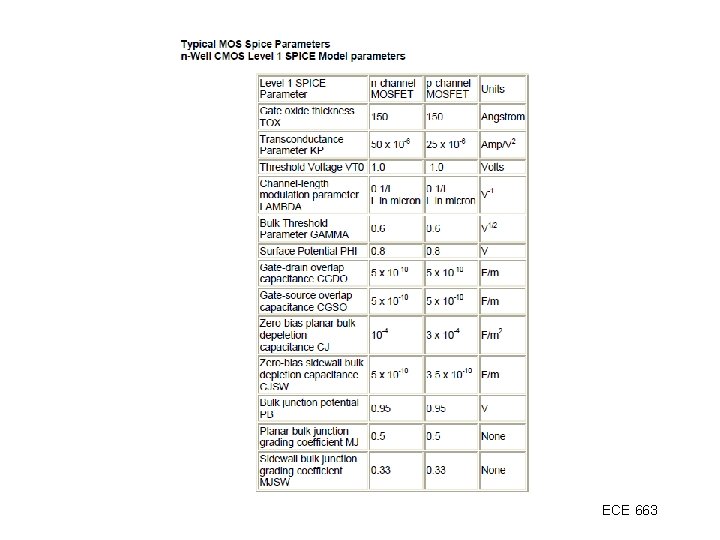
Comparison between different models Square Law Theory Bulk Charge Theory Body Coefficient Still not good below threshold or above saturation ECE 663

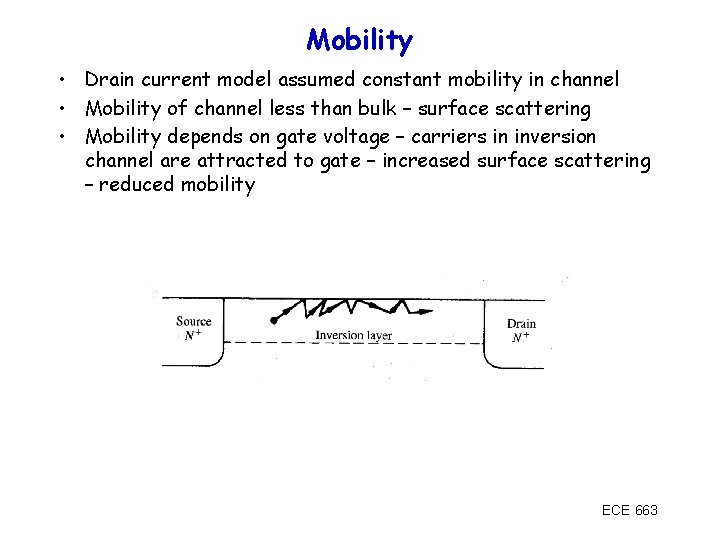
Mobility • Drain current model assumed constant mobility in channel • Mobility of channel less than bulk – surface scattering • Mobility depends on gate voltage – carriers in inversion channel are attracted to gate – increased surface scattering – reduced mobility ECE 663

Mobility dependence on gate voltage ECE 663

Sub-Threshold Behavior • For gate voltage less than the threshold – weak inversion • Diffusion is dominant current mechanism (not drift) ECE 663

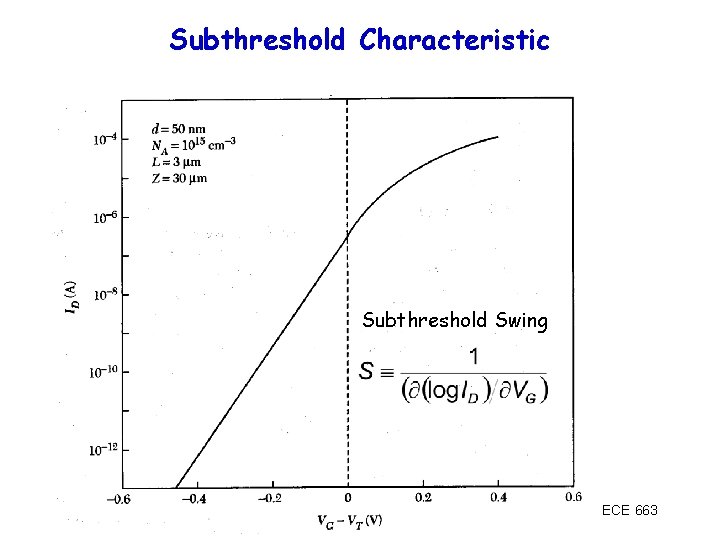
Sub-threshold We can approximate s with VG-VT below threshold since all voltage drops across depletion region • Sub-threshold current is exponential function of applied gate voltage • Sub-threshold current gets larger for smaller gates (L) ECE 663

Subthreshold Characteristic Subthreshold Swing ECE 663

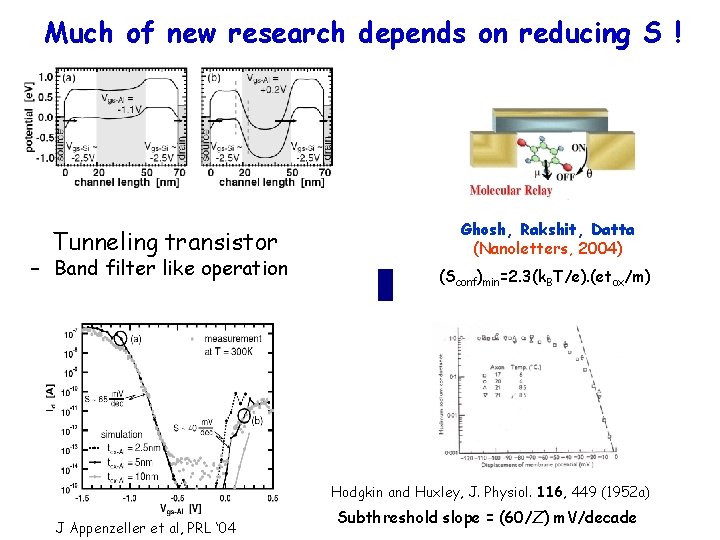
Much of new research depends on reducing S ! Tunneling transistor – Band filter like operation Ghosh, Rakshit, Datta (Nanoletters, 2004) (Sconf)min=2. 3(k. BT/e). (etox/m) Hodgkin and Huxley, J. Physiol. 116, 449 (1952 a) J Appenzeller et al, PRL ‘ 04 Subthreshold slope = (60/Z) m. V/decade

Much of new research depends on reducing S ! • Increase ‘q’ by collective motion (e. g. relay) Ghosh, Rakshit, Datta, NL ‘ 03 • Effectively reduce N through interactions Salahuddin, Datta • Negative capacitance Salahuddin, Datta • Non-thermionic switching (T-independent) Appenzeller et al, PRL • Nonequilibrium switching Li, Ghosh, Stan • Impact Ionization Plummer

More complete model – sub-threshold to saturation • Must include diffusion and drift currents • Still use gradual channel approximation • Yields sub-threshold and saturation behavior for long channel MOSFETS • Exact Charge Model – numerical integration ECE 663

Exact Charge Model (Pao-Sah) – Long Channel MOSFET http: //www. nsti. org/Nanotech 2006/WCM 2006 -BJie. pdf ECE 663

ECE 663