Morphological Image Processing Mathematical morphology is a branch

Morphological Image Processing § Mathematical morphology is a branch of image processing which has been successfully used to provide tools for representing, describing, and analyzing shapes in images. § Set Theory § Initially developed by Jean Serra in the early 1980 s § Named after the branch of biology that deals with the form and structure of animals and plants. 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 1

What is mathematical morphology? § Basic principle: the extraction of geometrical and topological information from an unknown set (an image) through transformations using another, well-defined, set, known as structuring element (SE). § In morphological image processing, the design of SEs, their shape and size, is crucial to the success of the morphological operations that use them. 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 2

Fundamental concepts and operations § Basic set operations: – Complement – Difference – Translation – Reflection 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 3
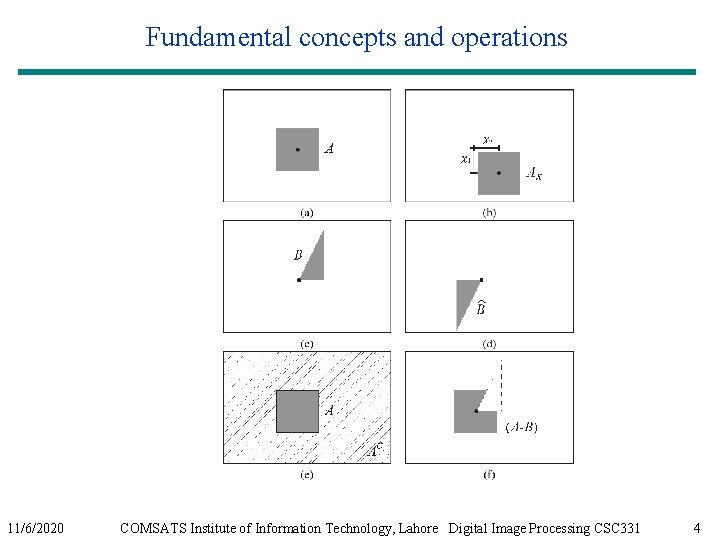
Fundamental concepts and operations 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 4

Fundamental concepts and operations § Logical equivalents of set theory operations – Intersection ~ logical AND – Similarly: • Complement ~ logical NOT • Union ~ logical OR • Difference ~ A AND (NOT B) 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 5
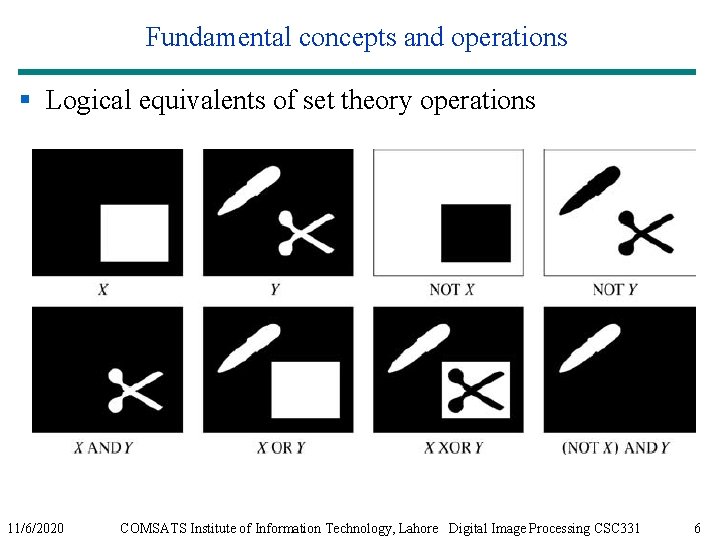
Fundamental concepts and operations § Logical equivalents of set theory operations 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 6

The structuring element § The structuring element (SE) is the basic neighborhood structure associated with morphological image operations. § It is usually represented as a small matrix, whose shape and size impact the results of applying a certain morphological operator to an image. § Although a structuring element can have any shape, its implementation requires that it be converted to a rectangular array. – For each array, the shaded squares correspond to the members of the SE whereas the empty squares are used for padding, only. 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 7
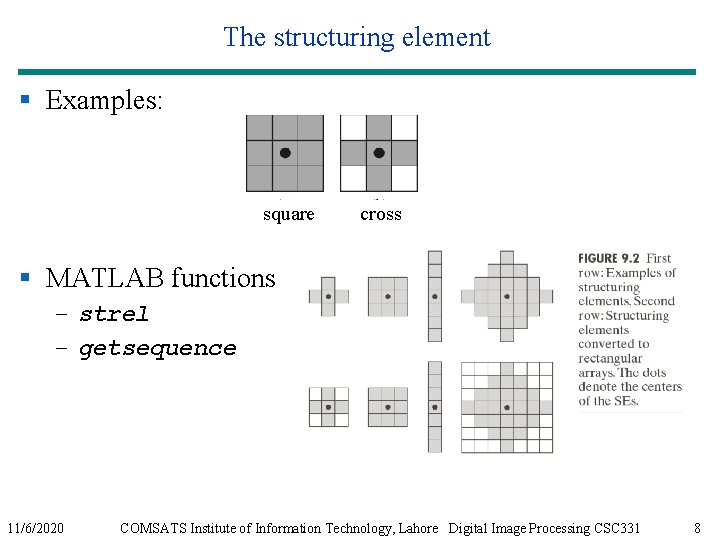
The structuring element § Examples: square cross § MATLAB functions – strel – getsequence 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 8
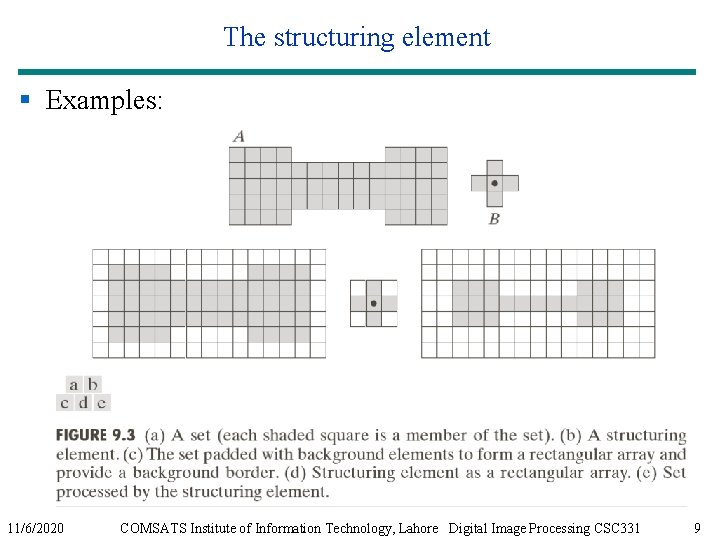
The structuring element § Examples: 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 9

Dilation and erosion § The two fundamental morphological image operations. – Dilation: a morphological operation whose effect is to “grow” or “thicken” objects in a binary image. • Simplest Application is “bridging the gaps”. • The extent and direction of this thickening is controlled by the size and shape of the structuring element. • Mathematically: 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 10
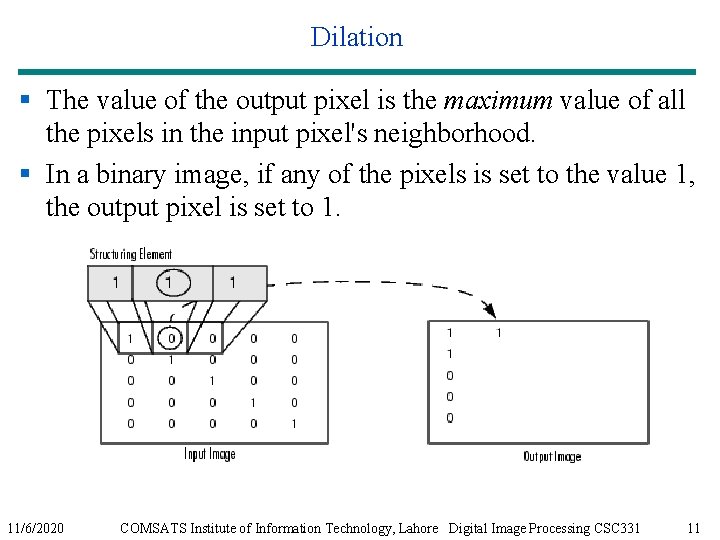
Dilation § The value of the output pixel is the maximum value of all the pixels in the input pixel's neighborhood. § In a binary image, if any of the pixels is set to the value 1, the output pixel is set to 1. 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 11

Dilation § Dilation – geometrical interpretation 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 12
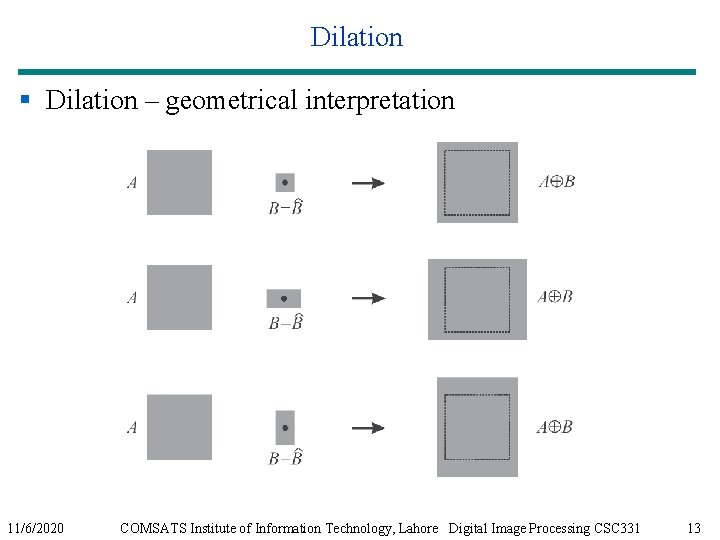
Dilation § Dilation – geometrical interpretation 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 13

Dilation § Dilation – Example 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 14

Dilation § Dilation – MATLAB example a = [0 0 0 1 1 1 0 0 0 0; 0; 0] se 1 = strel('square', 3) b = imdilate (a, se 1) se 2 = strel('rectangle', [1 3]) c = imdilate (a, se 2) 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 15

Erosion § Erosion: a morphological operation whose effect is to “shrink” or “thin” objects in a binary image. – The direction and extent of this thinning is controlled by the shape and size of the structuring element. – Mathematically: – B has to be contained in A = B not sharing any common elements with the background 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 16

Erosion § The value of the output pixel is the minimum value of all the pixels in the input pixel's neighborhood. § In a binary image, if any of the pixels is set to 0, the output pixel is set to 0. 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 17
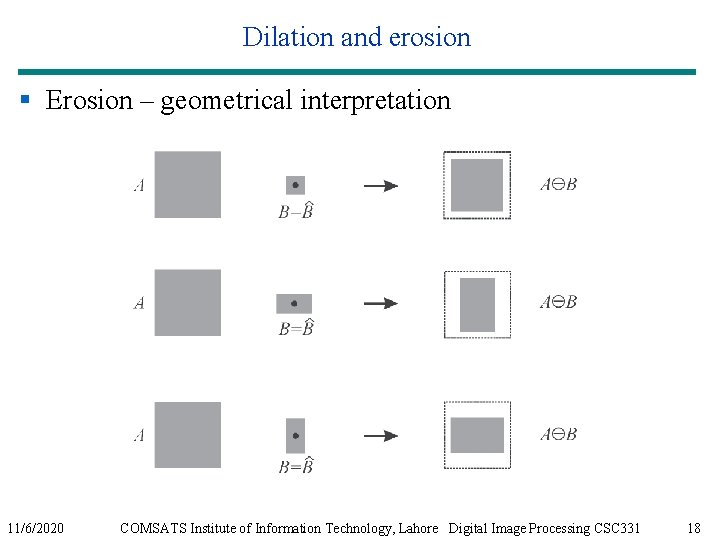
Dilation and erosion § Erosion – geometrical interpretation 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 18
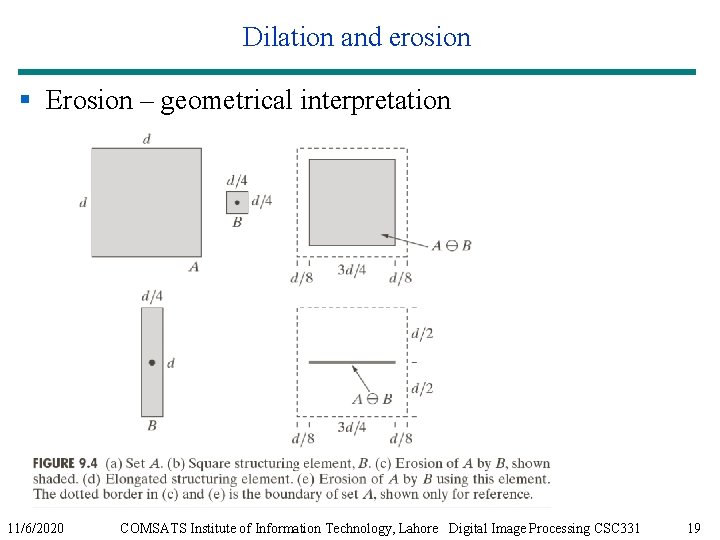
Dilation and erosion § Erosion – geometrical interpretation 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 19
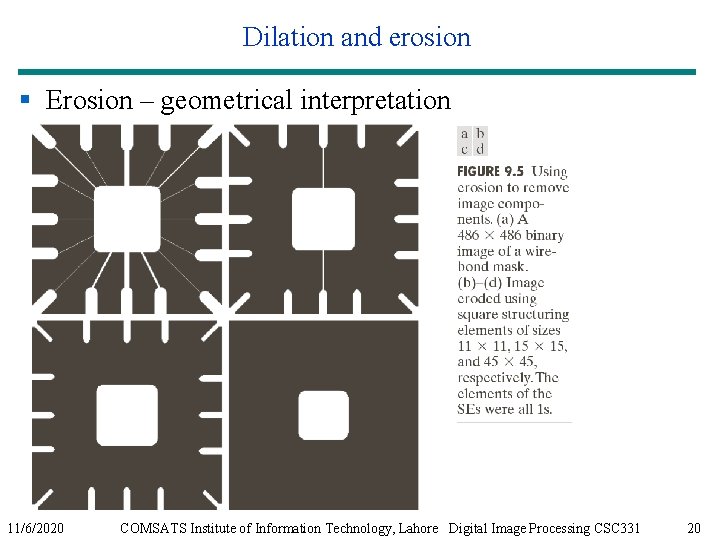
Dilation and erosion § Erosion – geometrical interpretation 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 20

Dilation and erosion § Erosion– MATLAB example a = [ 0 0 0 ; 0 1 1 1 0; 1 1 1 0 0; 0 1 1; 0 0 0] se 1 = strel('square', 3) b = imerode (a, se 1) se 2 = strel('rectangle', [1 3]) c = imerode (a, se 2) 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 21

Dilation and Erosion (Duality) § Erosion and dilation are dual operations 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 22

Compound Operations (Opening & Closing) Opening: erosion followed by dilation Mathematically: or: In MATLAB: imopen 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 23

Compound operations (Opening & Closing) § Closing: dilation followed by erosion § Mathematically: § In MATLAB: imclose 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 24

Compound Operations (Example) 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 25

Compound Operations (Example) 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 26

Compound Operations (Example) Operations supported by bwmorph 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 27

Basic Morphological Algorithms § § § § Boundary Extraction Hole Filling Extraction of Connected Components Thinning Thickening Skeletons Pruning Reconstruction 11/6/2020 COMSATS Institute of Information Technology, Lahore Digital Image Processing CSC 331 28
- Slides: 28