Morphological Image Processing c 2003 2006 by Yu

Morphological Image Processing (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing

Morphology l Morphology » The branch of biology that deals with the form and structure of organisms without consideration of function l Mathematical Morphology » Mathematical tool for processing shapes in image, including boundaries, skeletons, convex hulls, etc. » Use of set theoretical approach (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 2

Set Theory: Definitions and Notations l SET ( ) l » A collection of objects (elements) l l Subset ( ) Empty set ( ) (c) 2003 -2006 by Yu Hen Hu l Union ( ) » A B = { | A or B} l » Let A, B are two sets. If for every a A, we also have a B, then the set A is a subset of B, that is, A B » If A B and B A, then A = B. l » If A , then its complement set Ac = { | , and A} membership ( ) » If is an element (member) of a set , we write Complement set Intersection ( ) » A B = { | A and B} l Set difference (-) » BA = B Ac » Note that B-A A-B l Disjoint sets » A and B are disjoint (mutually exclusive) if A B= ECE 533 Digital Image Processing 3
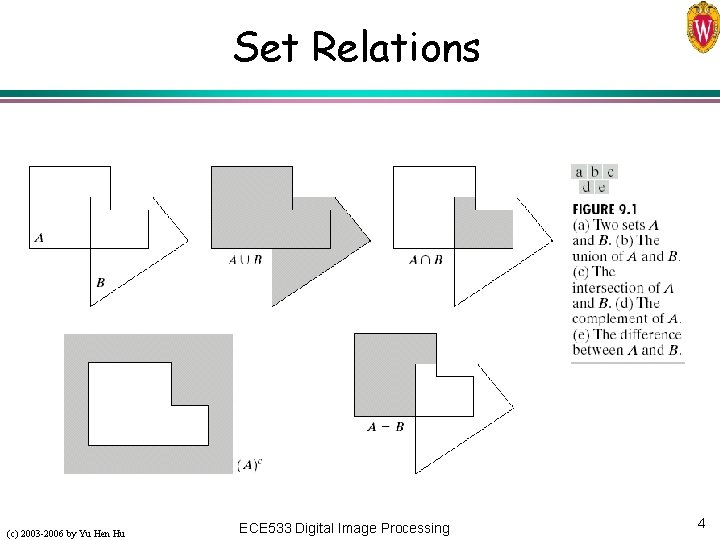
Set Relations (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 4
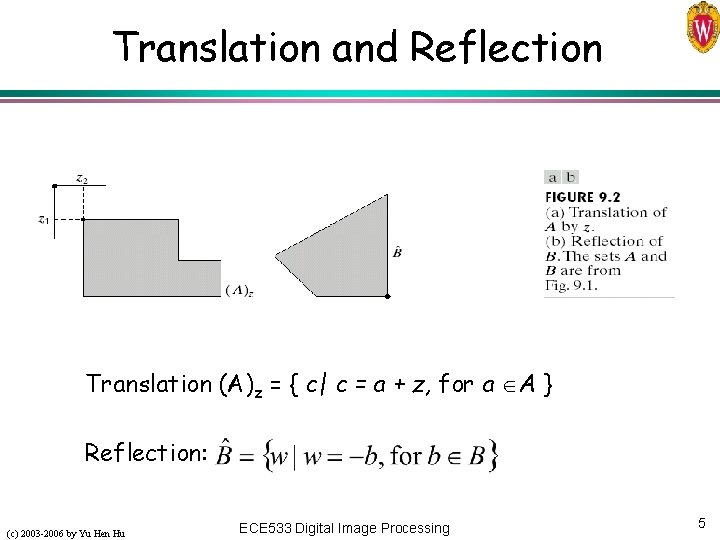
Translation and Reflection Translation (A)z = { c| c = a + z, for a A } Reflection: (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 5

Logic Operations Between Binary Images (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 6
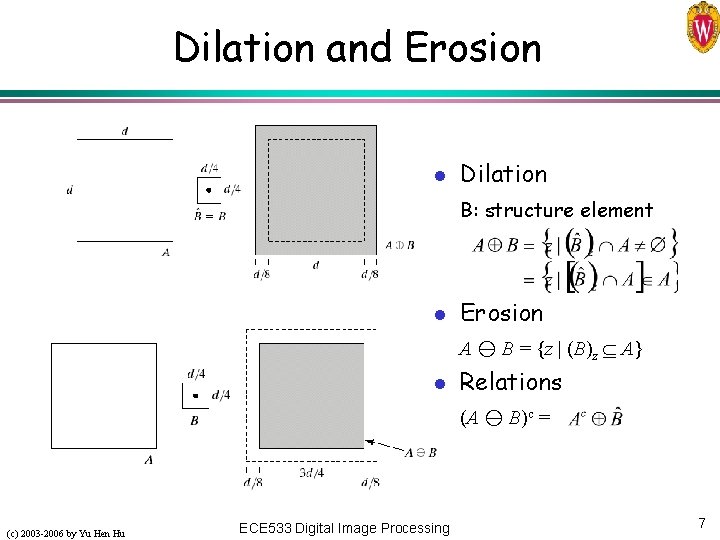
Dilation and Erosion l Dilation B: structure element l Erosion A B = {z | (B)z A} l Relations (A B)c = (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 7

Example of Dilation (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 8

Example of Erosion (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 9
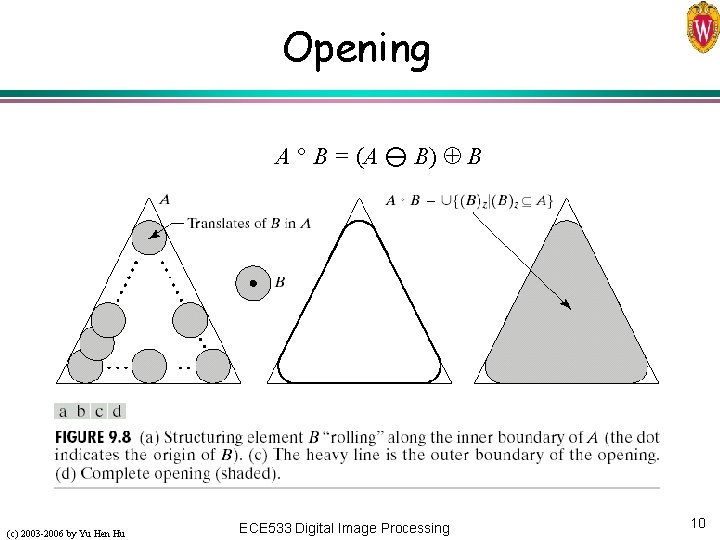
Opening A B = (A B) B (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 10
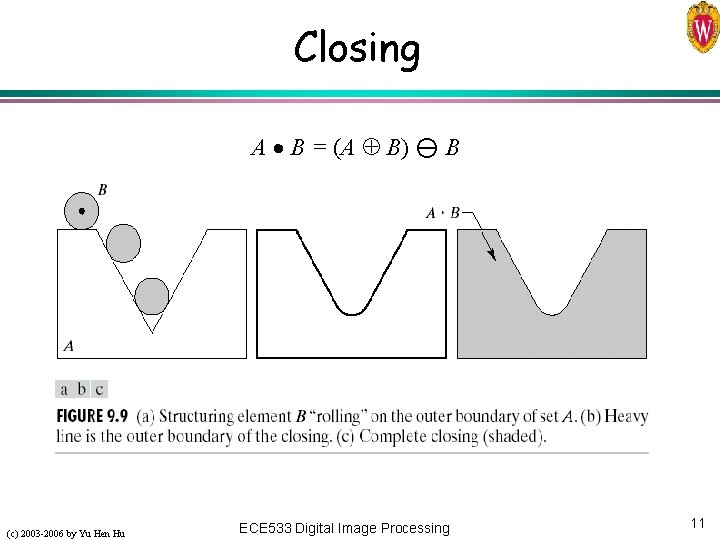
Closing A B = (A B) B (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 11
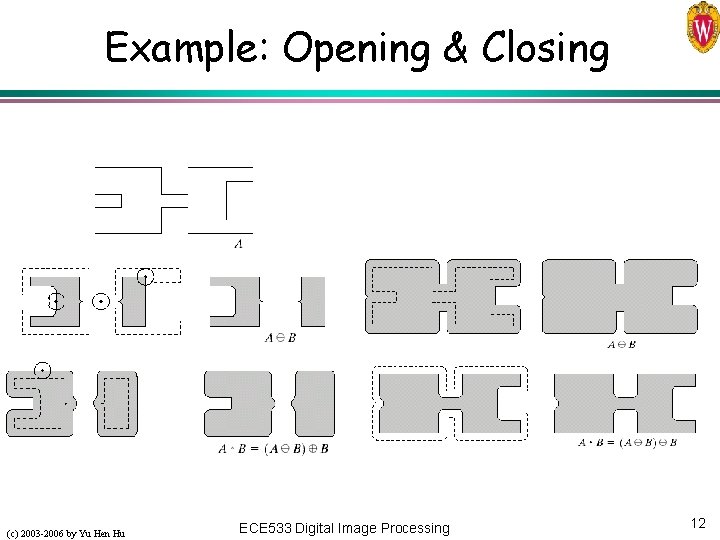
Example: Opening & Closing (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 12
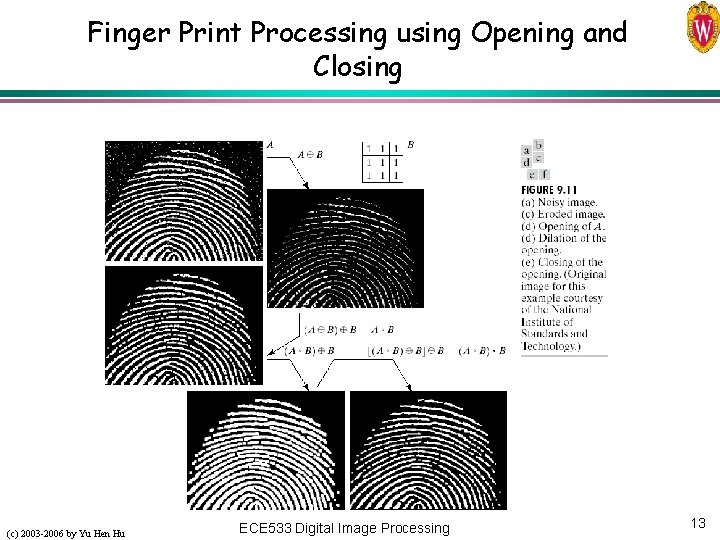
Finger Print Processing using Opening and Closing (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 13
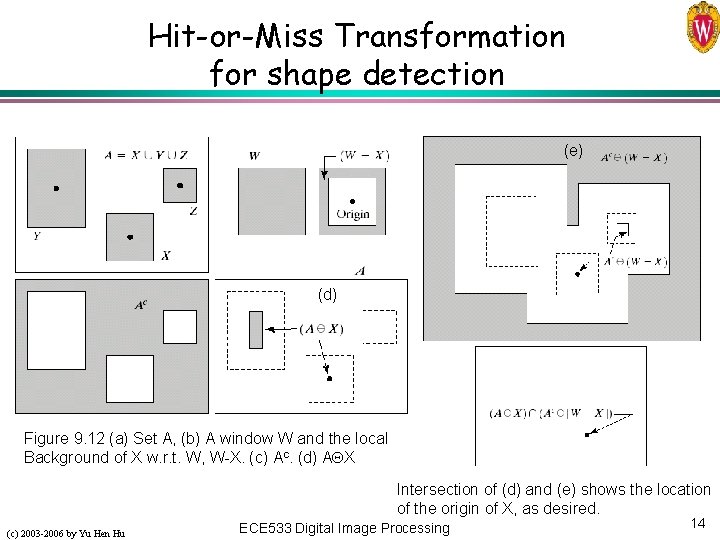
Hit-or-Miss Transformation for shape detection (e) (d) Figure 9. 12 (a) Set A, (b) A window W and the local Background of X w. r. t. W, W-X. (c) Ac. (d) A X Intersection of (d) and (e) shows the location of the origin of X, as desired. (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 14

Hit-or-Miss Transform l Denote B 1: object, B 2: local background of B 1, then, or l Reason to have a local background: » Two or more objects are distinct only if they form disjoint (disconnected) sets. This is guaranteed by requiring that each object have at least a one-pixel-thick background around it. (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 15

Hit-or-Miss Transform l l Previous example does not contain don’t care entries. In structure element » 1 – foreground » 0 – background » X – don’t care l l Hitnmiss. m » +1: foreground » -1: background » 0: don’t care Output is 1 if exact match of both foreground and background pixels. (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing Hitnmiss. m 16
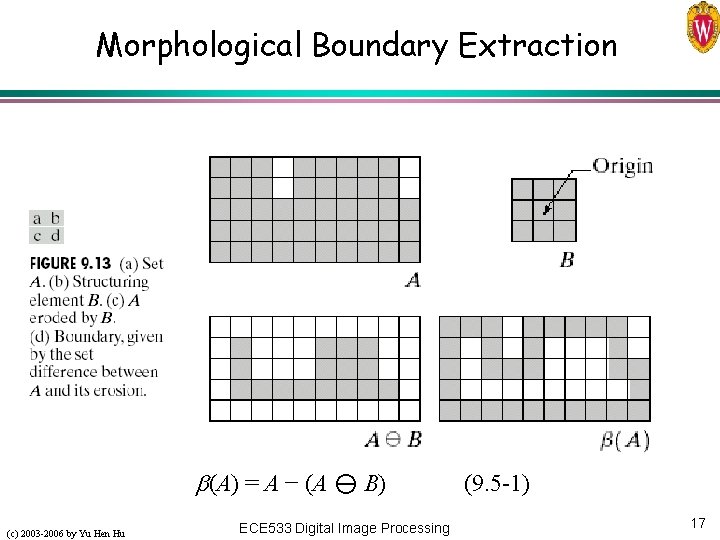
Morphological Boundary Extraction (A) = A − (A B) (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing (9. 5 -1) 17

Example of Boundary Extraction (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 18
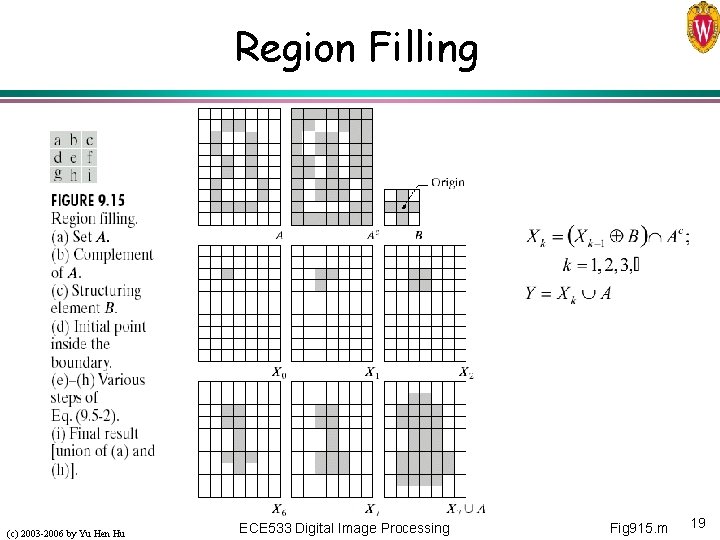
Region Filling (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing Fig 915. m 19

Region Filling Example (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 20
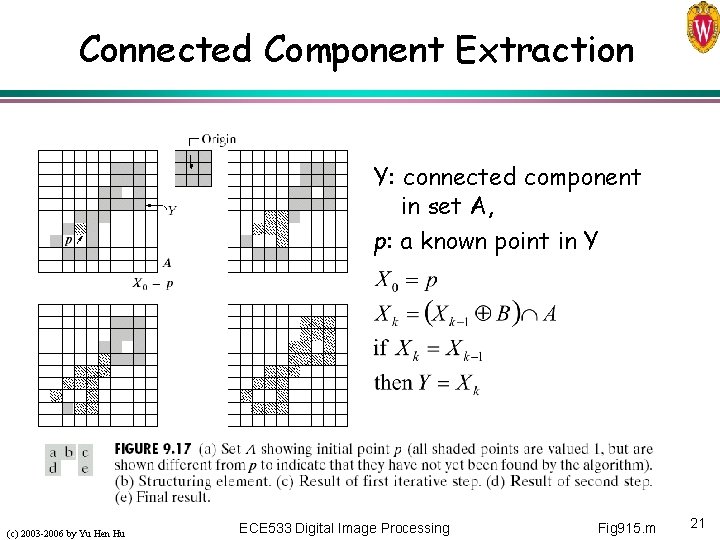
Connected Component Extraction Y: connected component in set A, p: a known point in Y (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing Fig 915. m 21

Thinning is often accomplished using a sequence of rotated structuring elements (a). Given a set A (b), results of thinning with first element is shown in (c), and the next 7 elements (d) – (i). There is no change between 7 th and 8 th elements, and no change after first 3 elements. Then it converges to a mconnectivity. (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing Fig 921. m 22
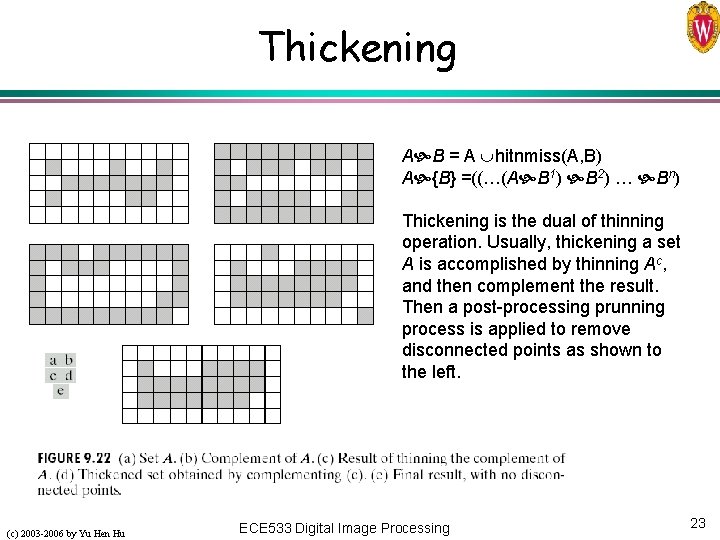
Thickening A B = A hitnmiss(A, B) A {B} =((…(A B 1) B 2) … Bn) Thickening is the dual of thinning operation. Usually, thickening a set A is accomplished by thinning Ac, and then complement the result. Then a post-processing prunning process is applied to remove disconnected points as shown to the left. (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 23
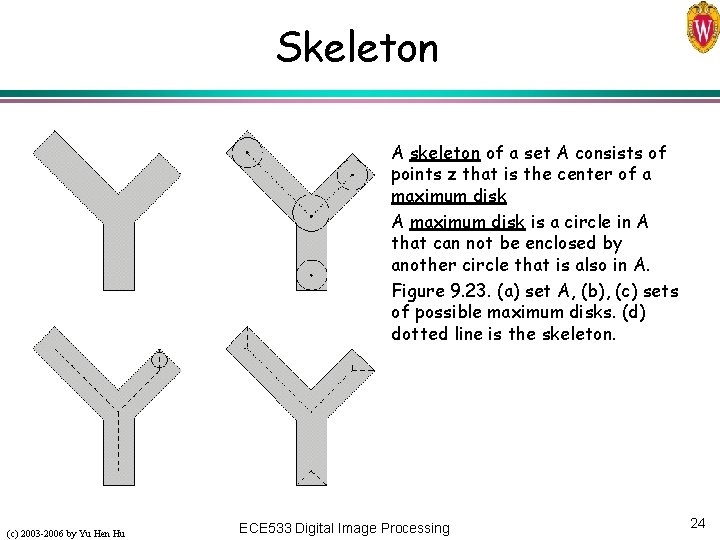
Skeleton A skeleton of a set A consists of points z that is the center of a maximum disk A maximum disk is a circle in A that can not be enclosed by another circle that is also in A. Figure 9. 23. (a) set A, (b), (c) sets of possible maximum disks. (d) dotted line is the skeleton. (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 24

Skeleton Equations l l Define k consecutive erosions of A as: A k. B = ( …(A B) B) …) B) (9. 5 -13) Sk(A) = (A k. B) − (A k. B) B (9. 5 -12) Let K = max{k | (A k. B) } (9. 5 -14) Then the skeleton can be found as: (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 25
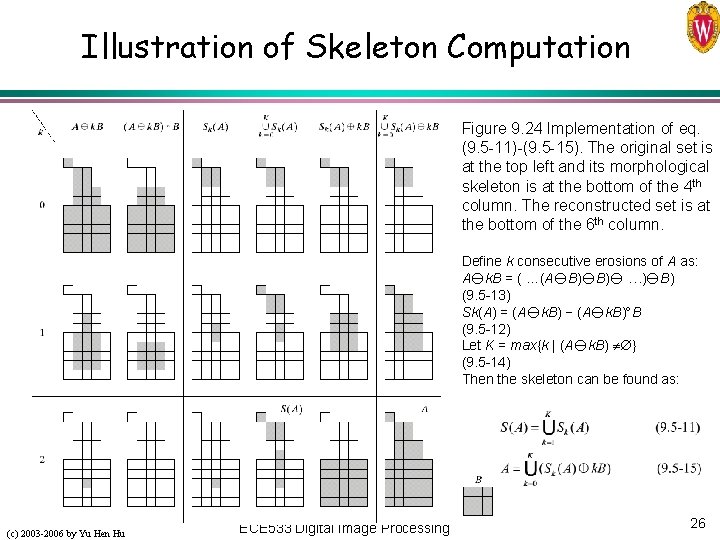
Illustration of Skeleton Computation Figure 9. 24 Implementation of eq. (9. 5 -11)-(9. 5 -15). The original set is at the top left and its morphological skeleton is at the bottom of the 4 th column. The reconstructed set is at the bottom of the 6 th column. Define k consecutive erosions of A as: A k. B = ( …(A B) B) …) B) (9. 5 -13) Sk(A) = (A k. B) − (A k. B) B (9. 5 -12) Let K = max{k | (A k. B) } (9. 5 -14) Then the skeleton can be found as: (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 26

Pruning (c) 2003 -2006 by Yu Hen Hu ECE 533 Digital Image Processing 27
- Slides: 27