More Trigonometry Section 4 2 Review Angles Standard

More Trigonometry!! Section 4 -2 Review Angles Standard Position Coterminal Angles Reference Angles Converting from Degrees – degrees, minutes, seconds (DMS)

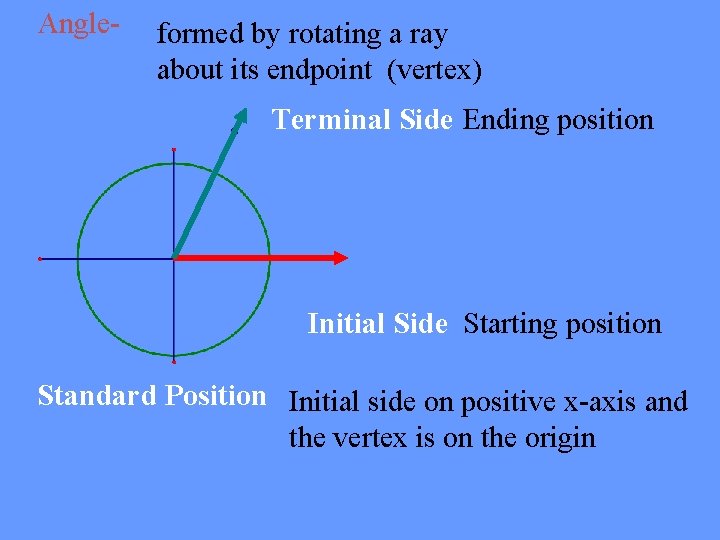
Angle- formed by rotating a ray about its endpoint (vertex) Terminal Side Ending position Initial Side Starting position Standard Position Initial side on positive x-axis and the vertex is on the origin

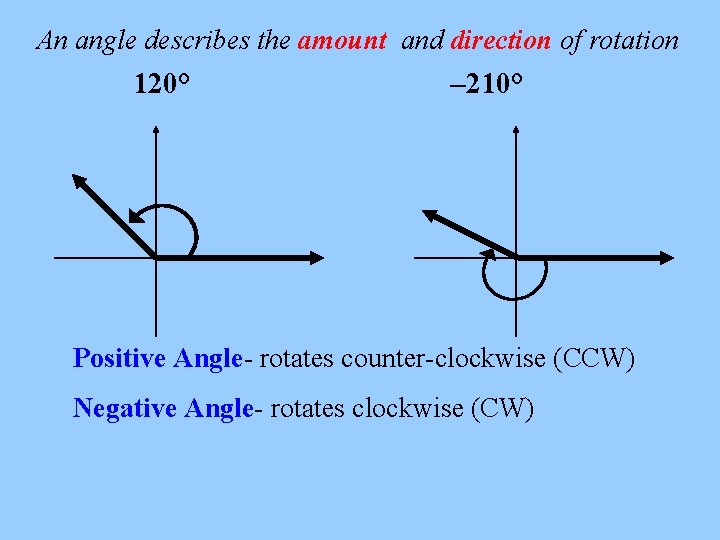
An angle describes the amount and direction of rotation 120° – 210° Positive Angle- rotates counter-clockwise (CCW) Negative Angle- rotates clockwise (CW)

Coterminal Angles: Two angles with the same initial and terminal sides Find a positive coterminal angle to 20º Find a negative coterminal angle to 20º Types of questions you will be asked: Identify a) ALL angles coterminal with 45º, then b) find one positive coterminal angle and one negative coterminal angle. a) 45º + 360 k (where k is any given integer). b) Some possible answers are 405º, 765º, - 315º, - 675º

Decimal Degrees (DD) • Decimal degrees are similar to degrees/ minutes/seconds (DMS) except that minutes and seconds are expressed as decimal values. • Decimal degrees make digital storage of coordinates easier and computations faster. 60. 34444 instead of 60° 20'40"

Converting from DMS to DD Express 36 50 10 as decimal degrees (DD) To complete the calculation, remember that … 1 degree = 60 minutes 1 minute = 60 seconds 1° = 60 1 = 60 3600 So … 1 degree = _____seconds THEREFORE …

Try this: Converting DMS to DD degrees seconds 60º 20'40" minutes 20 minutes. = 0. 33333 (20/60) 40 seconds = 0. 01111 (40/3600) Add up the degrees to get an answer: 60º + 0. 33333 + 0. 01111=60. 34444 DD

Converting from DD to DMS Express 50. 525 in degrees, minutes, seconds To reverse the process, we multiply by 60 instead. 50º +. 525(60) 50º + 31. 5 50º + 31 +. 5(60) 50 degrees, 31 minutes, 30 seconds

Homework Page 238 # 2 - 16 evens

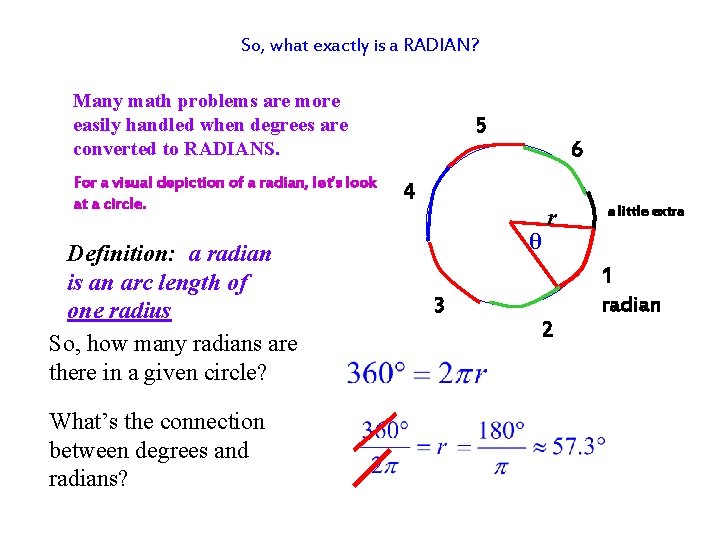
So, what exactly is a RADIAN? Many math problems are more easily handled when degrees are converted to RADIANS. For a visual depiction of a radian, let’s look at a circle. Definition: a radian is an arc length of one radius So, how many radians are there in a given circle? What’s the connection between degrees and radians? 5 6 4 θ 3 r 2 a little extra 1 radian

We can use the two ratios and degrees. to convert between radians Example: Change 330˚ to radians: In most cases, radians are left in terms of π Example: Convert radians to degree measure.

Two formulas to know: 1. Arc Length of a circle: S = rθ (θ in radians) Example: Given a central angle of 128 degrees, find the length of the intercepted arc in a circle of radius 5 centimeters. Round to nearest tenth. S = rθ 11. 2 cm 2. Area of a sector (slice of pie): A = ½ r 2θ (θ in radians) Example: Find the area of a sector of the central angle measures the radius of the circle is 16 inches. Round to nearest tenth. A = ½ r 2θ radians and

Linear & Angular Velocity Things that turn have both a linear velocity and an angular velocity.

Things that Turn - Examples tire on a car or bike buckets on a waterwheel teeth on a gear can on a kitchen cabinet lazy susan propeller on an airplane horse on a Merry-Go-Round fins on a fan or a windmill earth on its axis

Linear & Angular Velocity - Examples film on a projector or tape on a videotape turntable in a microwave oven blade on a lawnmower Earth around the sun seat on a Ferris wheel rope around a pulley a record on an old record player drum/barrel in a clothes dryer

Things that Turn - Examples lock on your locker hands on a clock roller brush on a vacuum cleaner tops & gyroscopes & dradle motor crankshaft blades in a blender roller skate wheels Carnival rides: tilt-a-whirl, scrambler, etc. weather vane washing machine agitator

Angular Velocity Definition: Angular Velocity (ω): the speed at which an angle opens. Remember: θ is in radians. Ex. 6 rev/min, 360°/day, 2π rad/hour

Angular Velocity Example: determine the angular velocity if 7. 3 revolutions are completed in 9 seconds. Round to nearest tenth. 1 revolution is 2π radians … so we’re talking about… Let’s use the formula:

Angular Velocity EXAMPLE 2: A carousel makes 2 5/8 rotations per minute. Determine the angular velocity of a rider on the carousel in radians per second.

Linear Velocity Definition: Linear Velocity: the speed with which An object revolves a fixed distance from a central point. If you already know the angular velocity, then … Ex. 55 mph, 6 ft/sec, 27 cm/min, 4. 5 m/sec

Linear Velocity In the carousel scenario, one of the animals is 20 feet from the center. What is its linear velocity?

Solution The cable moves at a fixed speed … a linear velocity. 5. 5 ft/sec