More Trigonometric Integrals Lesson 9 4 Recall Basic

More Trigonometric Integrals Lesson 9. 4

Recall Basic Identities • Pythagorean Identities • Half-Angle Formulas These will be used to integrate powers of sin and cos 2

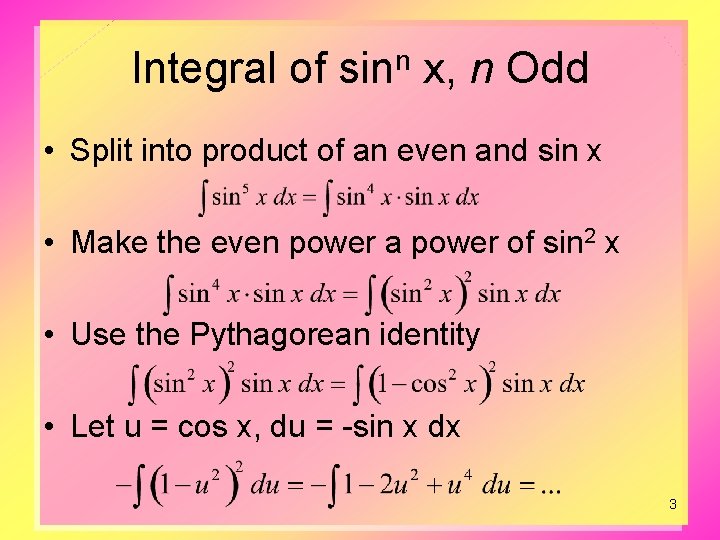
Integral of sinn x, n Odd • Split into product of an even and sin x • Make the even power a power of sin 2 x • Use the Pythagorean identity • Let u = cos x, du = -sin x dx 3

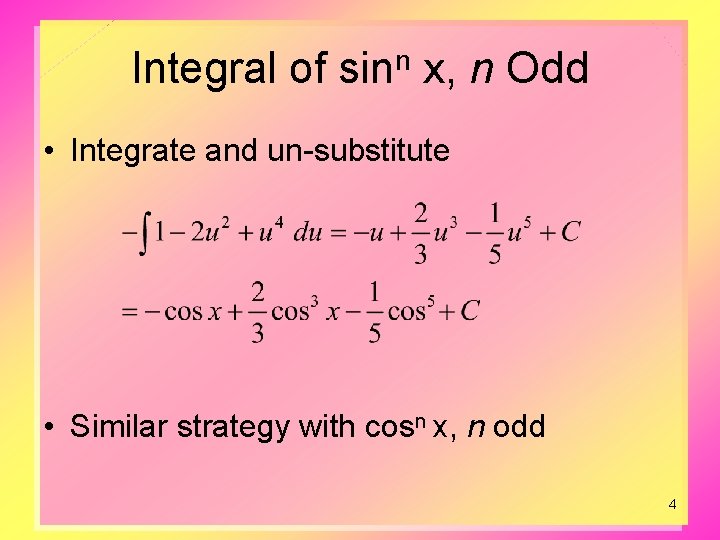
Integral of sinn x, n Odd • Integrate and un-substitute • Similar strategy with cosn x, n odd 4

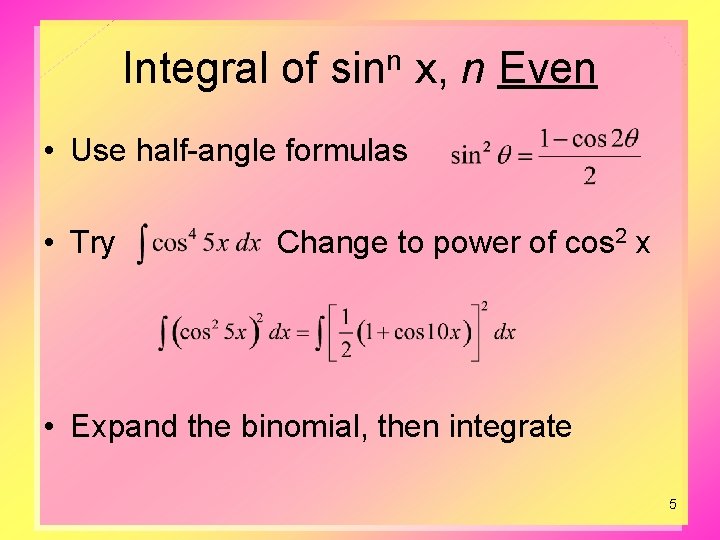
Integral of sinn x, n Even • Use half-angle formulas • Try Change to power of cos 2 x • Expand the binomial, then integrate 5

Combinations of sin, cos • General form Try with • If either n or m is odd, use techniques as before § § § Split the odd power into an even power and power of one Use Pythagorean identity Specify u and du, substitute Usually reduces to a polynomial Integrate, un-substitute 6

Combinations of sin, cos • Consider • Use Pythagorean identity • Separate and use sinn x strategy for n odd 7

Combinations of tanm, secn • When n is even Factor out sec 2 x § Rewrite remainder of integrand in terms of Pythagorean identity sec 2 x = 1 + tan 2 x § Then u = tan x, du = sec 2 x dx § • Try 8

Combinations of tanm, secn • When m is odd Note similar Factor out tan x sec x (for the du)strategies for integrals involving § Use identity sec 2 x – 1 = tan 2 combinations x for evenof cotm x and cscn x powers of tan x § Let u = sec x, du = sec x tan x § • Try the same integral with this strategy 9

Integrals of Even Powers of sec, csc • Use the identity sec 2 x – 1 = tan 2 x • Try 10

Assignment • Lesson 9. 4 • Page 376 • Exercises 1 – 33 odd 11