More Parameter Learning Multinomial and Continuous Variables Baran

More Parameter Learning, Multinomial and Continuous Variables Baran Barut CSE 970 – PATTERN RECOGNITION

OUTLINE § Multinomial Variables - Learning a Relative Frequency - Probability Intervals and Regions - Learning Parameters in a Bayesian Network - Missing Data Items - Variances in Computed Relative Frequencies § Continuous Variables - Normally Distributed Variable - Multivariate Normally Distributed Variable - Gaussian Bayesian Networks

§ Dirichlet: where Modeling our beliefs concerning relative frequencies!
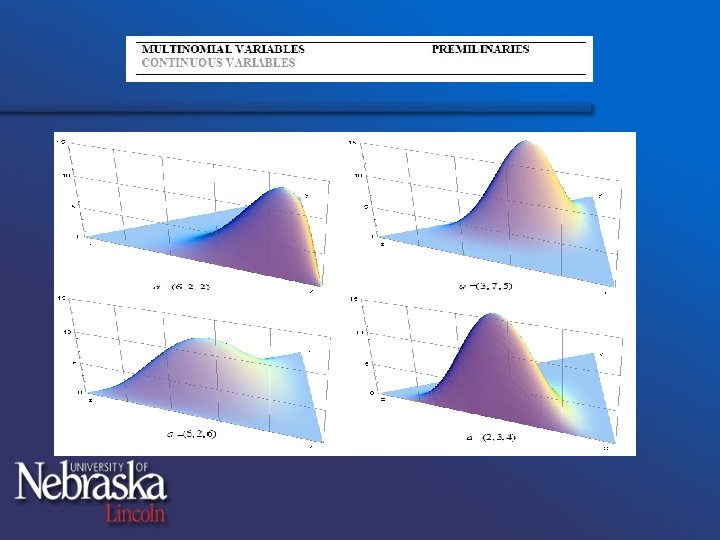

§ Introductory formulas: If we knew that the relative frequency of k’th outcome is fk :

§ The probability of data set: - D is a multinomial sample of size M governed by F - sk is the number of outcomes in d equal k

§ How to update the distribution function using a data set: § Updated probabilities of outcomes:

§ How confident are we about the estimate of the relative frequency fk?
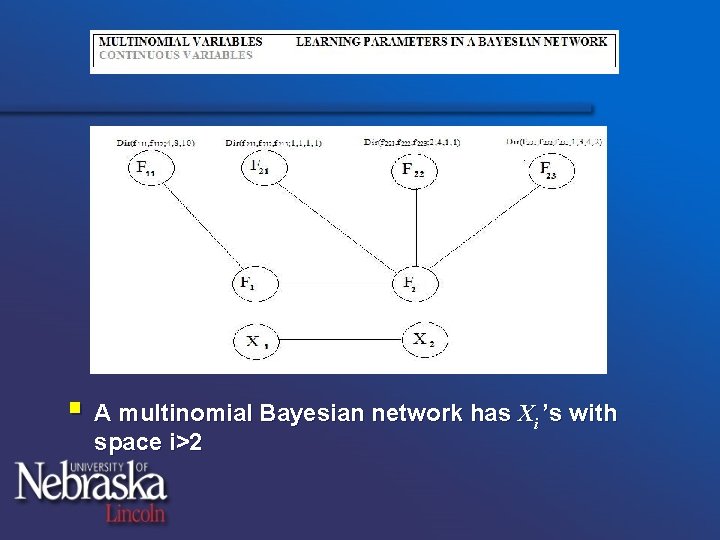
§ A multinomial Bayesian network has Xi ’s with space i>2

• Global independence of Fi’s • Local independence of Fij’s


§ Equivalent sample size, N § If G, F and N are specified, then or
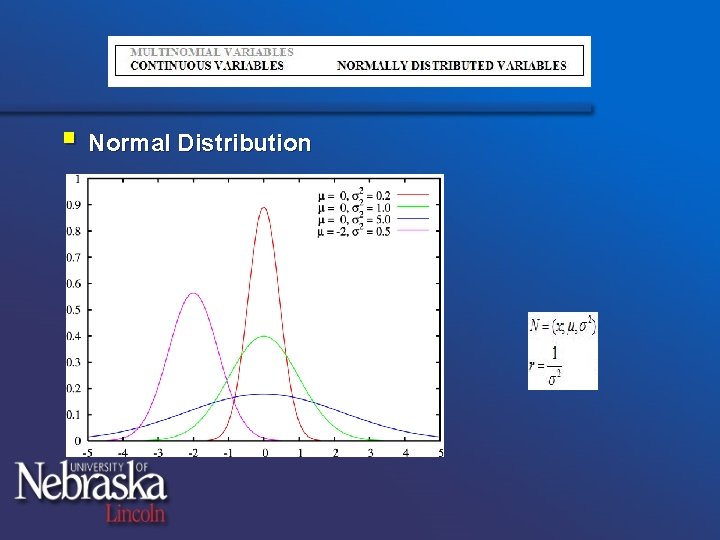
§ Normal Distribution

§ Unknown Mean and Known Variance

§ Sample of size M 1. Each outcome has real numbers as range 2. F = {A, r} and D is called a normal sample of size M with parameter {A, r}

§ posterior density of A

§assumptions about a hypothetical sample §r = 1 case § v = 0 case (no prior belief)

§Probality of the next outcome remember, initially: and

§ Gamma Distribution X 1, X 2, . . . , Xk are k-independent random variables with N(x; 0, σ2) and V= X 21+X 22+. . . +X 2 k , then: V has distribution gamma(v, k/2, 1/2 σ2)

§ Known Mean and Unknown Variance

§ Sample of size M 1. Each outcome has real numbers as range 2. F = {a, R} and D is called a normal sample of size M with parameter {a, R}

§ posterior density of r
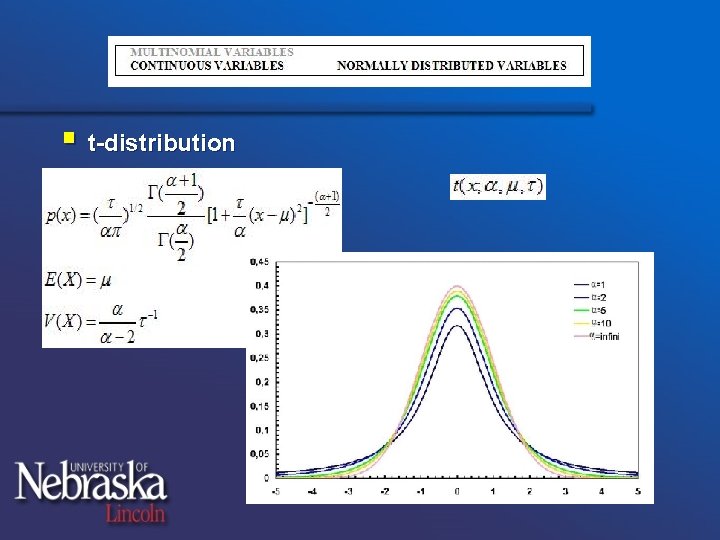
§ t-distribution

§ Unknown Mean and Unknown Variance

§ How to update? and

§meaning of the parameters v, μ μ is the mean of the hypothetical sample concerning value of A v is the size of the hypothetical sample concerning value of A

§meaning of the parameters β β is s of the hypothetical sample
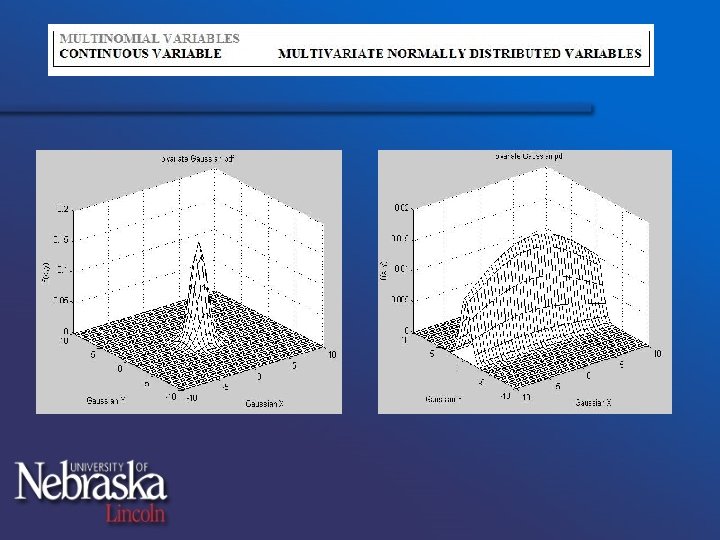

§bivariate normal distribution

§Vector Notation

§Positive definite – positive semi definite Symmetric n by n matrix A is positive definite if Symmetric n by n matrix A is positive semidefinite if

§Invertible If symmetric n by n matrix A is positive definite, then it is nonsingular. If Symmetric n by n matrix A is positive semidefinite but not positive definite, then it is singular.

§ Wishart-distribution

§ Multivariate t-distribution

§ Unknown Mean and Unknown Variance

§ How to update? and

§meaning of the parameters v, μ, β μ is the mean of the hypothetical sample concerning value of A v is the size of the hypothetical sample concerning value of A β is s of the hypothetical sample

§each node is a linear function of the values of the nodes that precede it in the ordering

§How to find the precision matrix
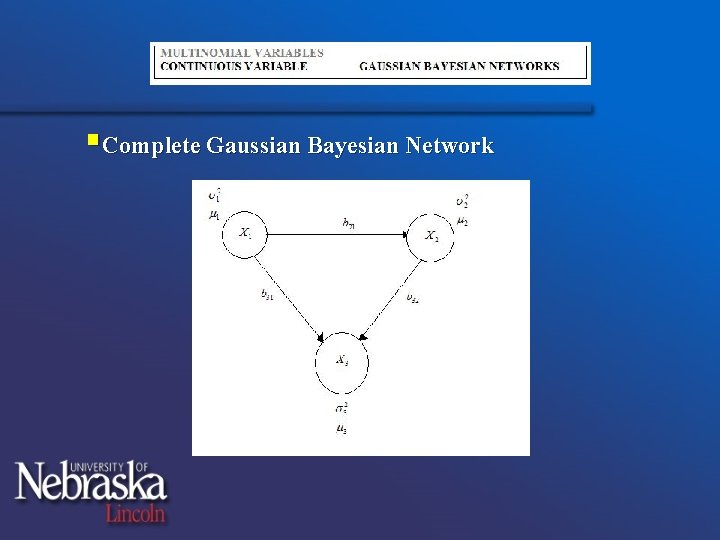
§Complete Gaussian Bayesian Network

§Covariance Matrix §What if b’s are 0?

§ How to update? and

§Approximations! Gaussian Bayesian Networks stand for N(x; μ, T-1) whereas x was given by t(x; α, μ, T) § We don’t assign distributions to Fi’s § We asses distributions for the random variables A, R
- Slides: 43