More on Linked List Algorithms Linked List and
























- Slides: 25

More on Linked List Algorithms

Linked List and Template • Remember the implementation of a double linked list we learned before. Some of methods are shown below class Node; typedef Node* Node. Ptr; class Node { public: int number; Node. Ptr next; Node. Ptr prev; }; class DLL { private: Node. Ptr top; void destroy. DLL(Node. Ptr&); public: DLL(); ~DLL(); void print. DLL(); void insert. DLL(int number); void destroy(Node. Ptr&); int search. DLL(int key); … … };

void DLL: : insert. DLL(int number) { Node. Ptr temp = top; temp = new Node; temp->next = top; temp->number = number; temp->prev = NULL; if (top != NULL) top->prev = temp; top = temp; } void DLL: : destroy. DLL(Node. Ptr& top) { Node. Ptr temp = top; while (top != NULL) { top = top->next; delete temp; temp = top; } top = NULL; } void DLL: : print. DLL() { Node. Ptr c=NULL, curr=top; while (curr != NULL) { cout << curr->number << "-->"; curr = curr->next; } cout << endl; } int DLL: : search. DLL(int key) { Node. Ptr curr = top; int count = 0; while (curr != NULL) { if (curr->number == key) count++; curr = curr -> next; } return count; } See: Example 1

• Consider the class node. It has three members: number next prev of type integer of type Node. Ptr • next and prev are just pointers to the successor and predecessor of a node respectively. • But number represents the actual content of a node. If this content has a different structure instead of being a simple integer, we need to create a different node class for creating different types of linked lists. • Fortunately with the help of template tools we learned in C++ we can make the content of a node to be of any data type • Next slide shows the doubly linked list structure with template

template <class T> class Node { public: T element; Node<T> *next; Node<T> *prev; }; See: Example 2 template <class T> class DLL { private: Node<T> *top; public: DLL(); ~DLL(); void destroy. DLL( Node<T> *&); void print. DLL(); void insert. DLL(T obj); bool search. DLL(T key); …. …. };

template <class T> void DLL<T>: : insert. DLL(T obj) { Node<T> *temp = top; temp = new Node<T>; temp->next = top; temp->element = obj; temp->prev = NULL; if (top != NULL) top->prev = temp; top = temp; } template <class T> bool DLL<T>: : search. DLL(T key) { Node<T> *curr = top; while (curr != NULL) { if (curr->element == key) return true; curr = curr -> next; } return false; } template <class T> void DLL<T>: : print. DLL() { Node<T> *curr=NULL; cout << endl; curr = top; while (curr != NULL) { cout << curr->element << "-->"; curr = curr->next; } cout << endl; } template <class T> void DLL<T>: : destroy. DLL(Node<T> *&top) { Node<T> *temp = top; while (top != NULL) { top = top->next; delete temp; temp = top; } top = NULL; }

Skip Lists • The serious drawback with the linked list is that to search an element we need to do sequential scanning of the linked list • One way to solve this problem is to order the list to speed up searching, but sequential search is still required. • The Skip List is an interesting variant of ordered linked list which makes such a non-sequential search possible • In the skip list method • Every node is linked (1 2 3, … ) • Every second node is linked (1 3 5 7, …) • Every fourth node is linked (1 5 9 …) • Every eighth node is linked (1 9 17 25, …) • Every sixteenth node is linked (1 17 33, …) • ….

• Therefore, a node may have different levels of pointers. • The following shows an example of a skip list. This type of skip list is called evenly spaced skip list

• Suppose we are looking for number 16 in the list • Level 4 in the root node is tried first and we follow the link realizing that 22 > 16. • Then level 3 in the root node is tried and we follow the link to 10 and then from 10 to 22 realizing that 22>16 • Next we set the pointer to the last valid node (in this case node 10) we visited but we try next level. (level 2 in this case) • From 10 we get to 17 and 17> 16 • So we stay at node 10 again and we try the first level (level 1) • We follow the link to 12 and then 17 and we realize that 17>16 • Since we cannot go any lower, we conclude that 16 is not in the list

• Searching will improve with skip list method relative to the regular linked list • But what about insert and delete? • If we insert a node or delete a node from the list, the whole structure changes. • The skip list we discussed was a type of evenly spaced nodes of different levels. Skip lists can be made of unevenly spaced nodes of different levels as shown in the next slide

• Making the skip list unevenly spaced with multiple levels, insert becomes simple and restructuring is not required • Deleting still needs a bit of work. When we delete a node x, we need to make sure that at all levels predecessors of node x are properly connected to the successors of node x • For example if we delete node 17, we need to make sure that node 8 is connected to node 28, node 10 is connected to node 22 and node 12 is connected to node 19

Self-Organizing Lists • Other methods to improve the efficiency of the search in the linked list is to dynamically organize the linked list in certain order • This organization depends on the configuration of the data, thus the stream of the data requires reorganizing the nodes already on the list • Several ways to reorganize the nodes are: • Move to the front method • Transpose method • Count method and • Ordering method

• Move to the front method: • After the desired element is located, put it at the beginning of the list • Transpose method: • After the desired element is located, swap it with its predecessor unless it is at the head of the list • Count Method: • Order the list by the number of times elements are being accessed • Ordering Method: • Order the list based on ascending or descending order

Example of Move-to-front Method • Suppose a set data A, B, C, D, and E are sent to the system. Using Move-to-front technique we insert an element if it is not in the list or move it to the front if it does already exist in the list: • Suppose some data arrive in this order: ACBCDADACACCEE

Example of Transpose Method • Suppose a set data A, B, C, D, and E are sent to the system. Using Transpose technique we insert an element if it is not in the list or swap it with its predecessor if it is already in the list • Suppose some data arrive in this order: ACBCDADACACCEE

Example of Count Method • Suppose a set data A, B, C, D, and E are sent to the system. Using Count technique we sort the elements based on the number of times that have been accessed • Suppose some data arrive in this order: ACBCDADACACCEE

Example of Ordering Method • Suppose a set data A, B, C, D, and E are sent to the system. Using Ordering technique we sort the elements in ascending order (in this example) • Suppose some data arrive in this order: ACBCDADACACCEE

• With the first three methods, we try to locate the elements most likely to be looked for near the beginning of the list • Every method except the ordering approach may require the search for an element to go to the end of the list • It is important to see how the data in your environment arrive the system. Then based on the behavior of the data, you can choose the best method of searching to implement for your linked list

Sparse Table • In many applications, the choice of table seems to be the most natural one but space consideration may also be an important factor to be considered • Suppose we want to store grades of all students in a university for a certain semester • Suppose there are 8000 students and 300 classes (courses) • One way to do this is to create two dimensional table making the Student-Ids as the columns and Class-Ids (course Number) to be the rows of the array. • Then we record the student’s grades in array cells

Students • For example, this table shows that the student with Student-Id 5206 has received d ( grade B) in the course with course-Id 30

• Assuming that every student on average can take five courses per semester. In this case, we would have 300 - 5 = 295 empty cells per column • Since there are 8000 columns, 8000*295 cells would be unused which is waste of a lot of space • Another solution is to create two 2 -dimensional arrays: • One is array of Classes. Takes where the columns represent the student-Ids and rows would be the maximum number of courses that can be possibly taken by the students • Second is array of Student. In. Classes where the columns are the Course-Ids and rows refer to the maximum number of students per class

Classes. Taken • The Classes. Taken array shows that the student with Student-Id 5207 has taken 3 courses with course Ids 290, 115, and 116 and has received grades e, a, and d respectively. Students. In. Classes • The Students. In. Classes array shows that course 115 have been taken by three students with students Ids 3078, 404, and 5207. These students have received grades a, e, and f in this course respectively.

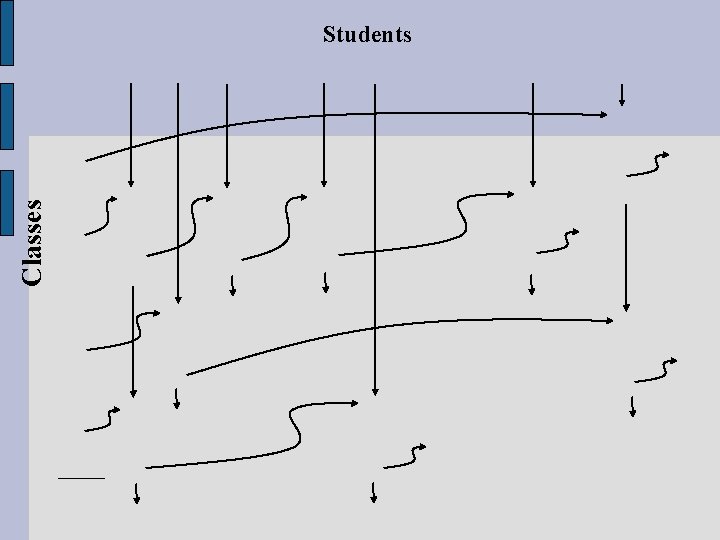
• Although the numbers of free cells have been reduced a lot, we still have a lot of free spaces. • Further, the major limitation of the Classes. Taken is that no student can take more than 8 courses per term. Similarly, in Students. In. Classes array, we must limit the enrollment of each course to 250 students per class • If space is our main concern, the best solution is to reduce the wasted space as much as possible without having too much effect in the efficiency of search. • The next slide shows this sparse table using the two-dimensional linked list techniques

Classes Students

• As you see in the slide, Two two-Dimensional arrays of linked list can be used • Each cell of the array class is a pointer to a linked list of students taking a class and each cell of the array students indicates a linked list of classes taken by a student • The linked lists contain nodes of five members: student-Id, Course-Id, the grade, a pointer to next student and a pointer to next class • Note that in this method we dynamically obtain space (creating a node) in memory only if we require that node to store the related information