More Graph Algorithms Minimum Spanning Trees Shortest Path

More Graph Algorithms Minimum Spanning Trees, Shortest Path Algorithms

Spanning Tree • Definition – A spanning tree of a graph G is a tree (acyclic) that connects all the vertices of G once • i. e. the tree “spans” every vertex in G – A Minimum Spanning Tree (MST) is a spanning tree on a weighted graph that has the minimum total weight Where might this be useful? Minimum material to connect nodes and also approximation for some hard problems.

Sample MST • Which links to make this a MST? Optimal substructure: A subtree of the MST must in turn be a MST of the nodes that it spans. This idea is common in recursion and dynamic programming.

MST Claim • Claim: Say that M is a MST – If we remove any edge (u, v) from M then this results in two trees, T 1 and T 2. – T 1 is a MST of its subgraph while T 2 is a MST of its subgraph. – Then the MST of the entire graph is T 1 + T 2 + the smallest edge between T 1 and T 2 – If some other edge was used, we wouldn’t have the minimum spanning tree overall

Greedy Algorithm • We can use a greedy algorithm to find the MST – A greedy algorithm is one that makes what looks like the best decision at a point in time and never backtracks to undo that decision – Two common algorithms • Kruskal • Prim

Kruskal’s MST Algorithm • Idea: Greedily construct the MST – Go through the list of edges and make a forest that is a MST – At each vertex, sort the edges – Edges with smallest weights examined and possibly added to MST before edges with higher weights – Edges added must be “safe edges” that do not ruin the tree property.

Kruskal’s Algorithm Kruskal(G, w) ; Graph G, with weights w A ¬ {} ; Our MST starts empty for each vertex v ÎV [G ] do Make -Set(v) ; Make each vertex a set Sort edges of E by increasing weight for each edge ( u, v ) Î E in order ; Find-Set returns a representative (first vertex) in the set do if Find -Set(u) ¹ Find-Set(v) then A ¬ A È {( u, v )} Union(u, v) ; Combines two trees return A

Kruskal’s Example • A={ }, Make each element its own set. {a} {b} {c} {d} {e} {f} {g} {h} • Sort edges. • Look at smallest edge first: {c} and {f} not in same set, add it to A, union together. • Now get {a} {b} {c f} {d} {e} {g} {h}

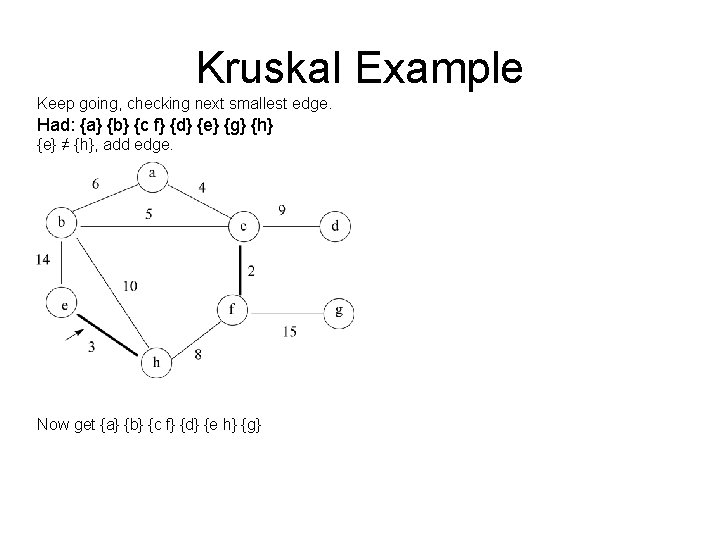
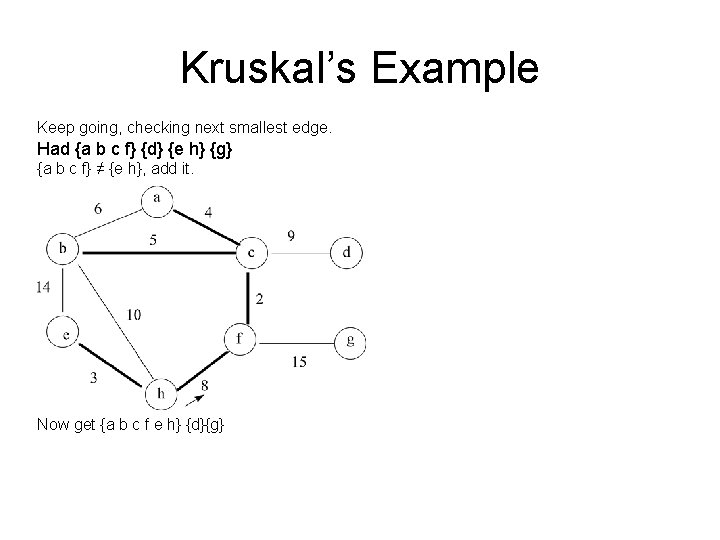
Kruskal Example Keep going, checking next smallest edge. Had: {a} {b} {c f} {d} {e} {g} {h} {e} ≠ {h}, add edge. Now get {a} {b} {c f} {d} {e h} {g}

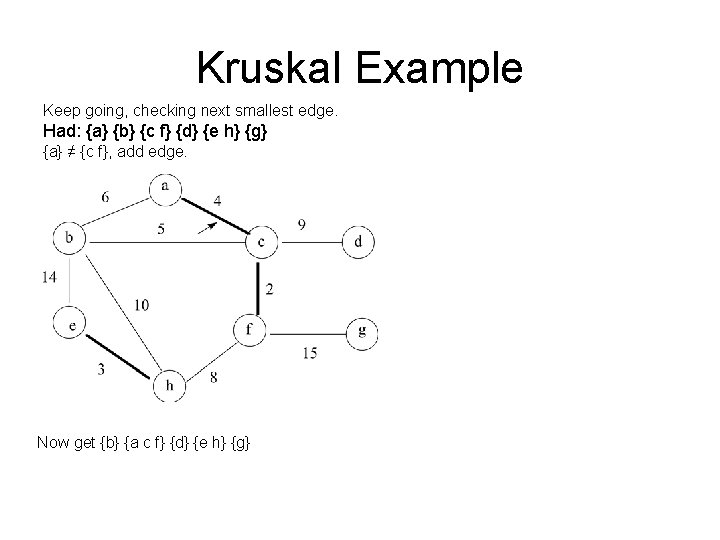
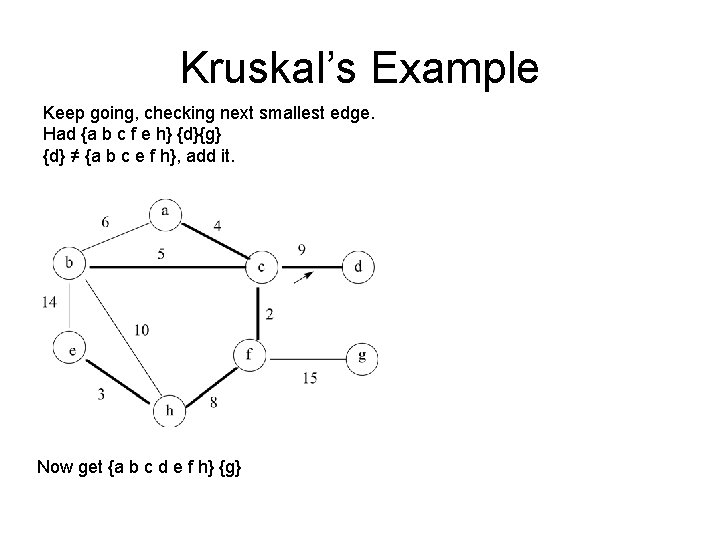
Kruskal Example Keep going, checking next smallest edge. Had: {a} {b} {c f} {d} {e h} {g} {a} ≠ {c f}, add edge. Now get {b} {a c f} {d} {e h} {g}

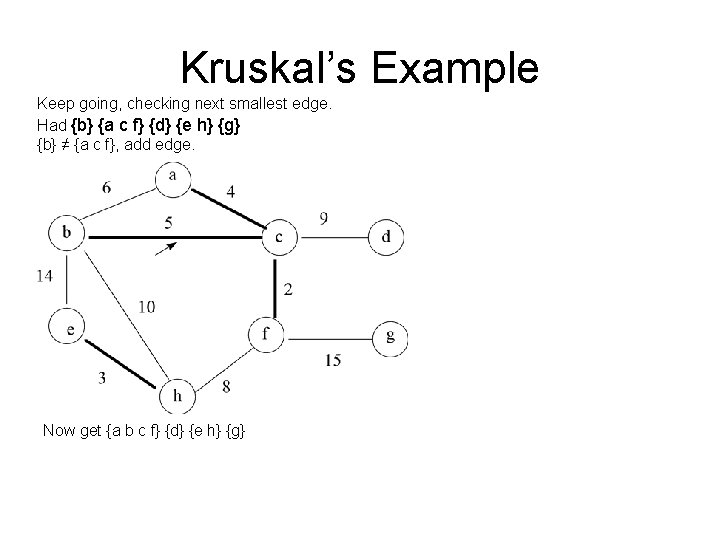
Kruskal’s Example Keep going, checking next smallest edge. Had {b} {a c f} {d} {e h} {g} {b} ≠ {a c f}, add edge. Now get {a b c f} {d} {e h} {g}

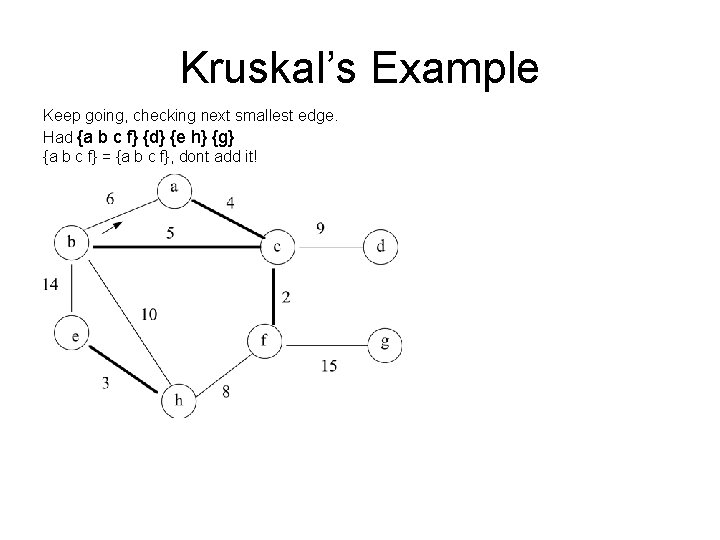
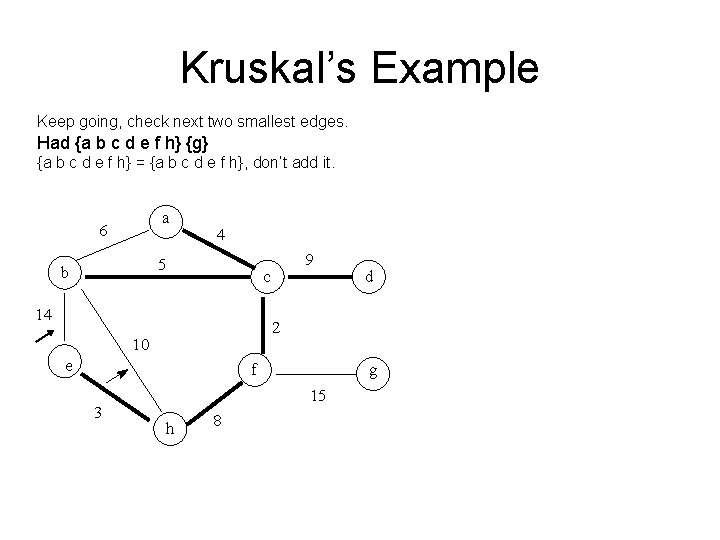
Kruskal’s Example Keep going, checking next smallest edge. Had {a b c f} {d} {e h} {g} {a b c f} = {a b c f}, dont add it!

Kruskal’s Example Keep going, checking next smallest edge. Had {a b c f} {d} {e h} {g} {a b c f} ≠ {e h}, add it. Now get {a b c f e h} {d}{g}

Kruskal’s Example Keep going, checking next smallest edge. Had {a b c f e h} {d}{g} {d} ≠ {a b c e f h}, add it. Now get {a b c d e f h} {g}

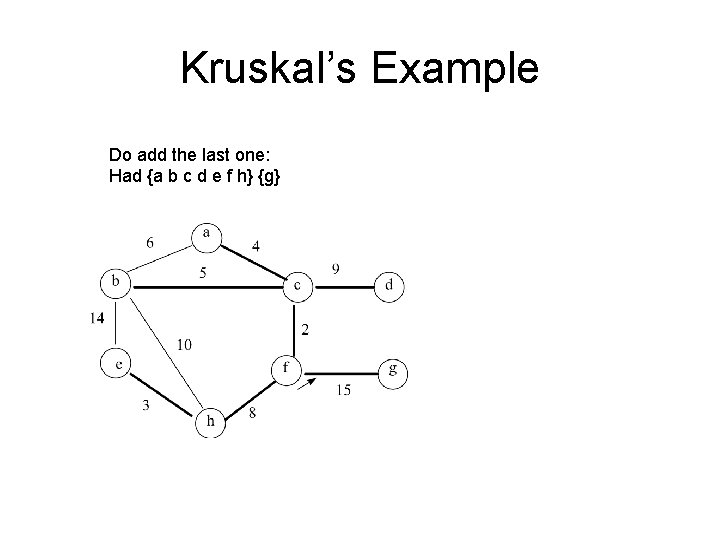
Kruskal’s Example Keep going, check next two smallest edges. Had {a b c d e f h} {g} {a b c d e f h} = {a b c d e f h}, don’t add it. a 6 4 5 b 9 c 14 2 10 e f 3 d g 15 h 8

Kruskal’s Example Do add the last one: Had {a b c d e f h} {g}

Runtime of Kruskal’s Algo • Runtime depends upon time to union sets, find set, make set • There are many ways to implement sets • One way: number each vertex and use an array – Member array identifies the set for each vertex member[ ] : member[i] is a number j such that the ith vertex is a member of the jth set; Assume array starts at index 1 – Example member[ ] = {1, 4, 1, 2, 2} indicates the sets S 1={1, 3}, S 2={4, 5} and S 4={2}; i. e. position in the array gives the set number. Idea similar to counting sort, up to number of edge members.

Set Operations • Given the Member array • Make-Set(v) member[v] = v 1 2 3 member = [1, 2, 3] ; {1} {2} {3} Make-Set runs in constant running time for a single set. Need O(v) for all vertices. • Find-Set(v) Return member[v] find-set(2) = 2 Find-Set runs in constant time. • Union(s 1, s 2) for i=1 to n if member[i] = s 1 then member[i]=s 2 Union(2, 3) member = [1, 3, 3] ; {1} {2 3} Scan through the member array and update old members to be the new set. Running time O(n), length of member array.

Overall Runtime O(V) O(Elg. E) – using heapsort O(E) O(1) O(V) Total runtime: O(V)+O(Elg. E)+O(E*(1+V)) = O(E*V) Later we may discuss a disjoint set algorithm with path compression and union by rank that will result in O(E*lg. V) time

Prim’s MST Algorithm • Also greedy, like Kruskal’s • Will find a MST but may differ from Prim’s if multiple MST’s are possible MST-Prim(G, w, r) ; Graph G, weights w, root r Q ¬ V[G] for each vertex u Î Q do key[u] ¬ ¥ ; infinite “distance” key[r] ¬ 0 ; key determines what to extract from the Min Queue P[r] ¬ NIL while Q is not empty do u ¬ Extract-Min(Q) ; remove closest node ; Update children of u so they have a parent and a min key val ; the key is the weight between node and parent for each v ÎAdj[u] do if v ÎQ & w(u, v)<key[v] then P[v] ¬ u key[v] ¬ w(u, v)

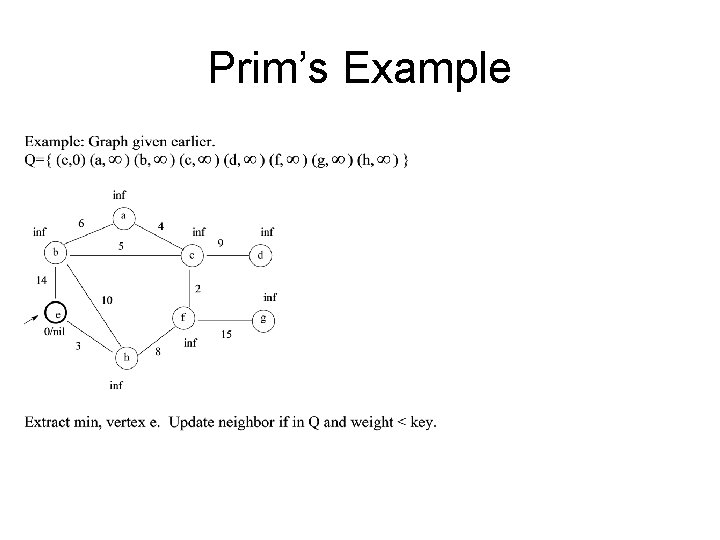
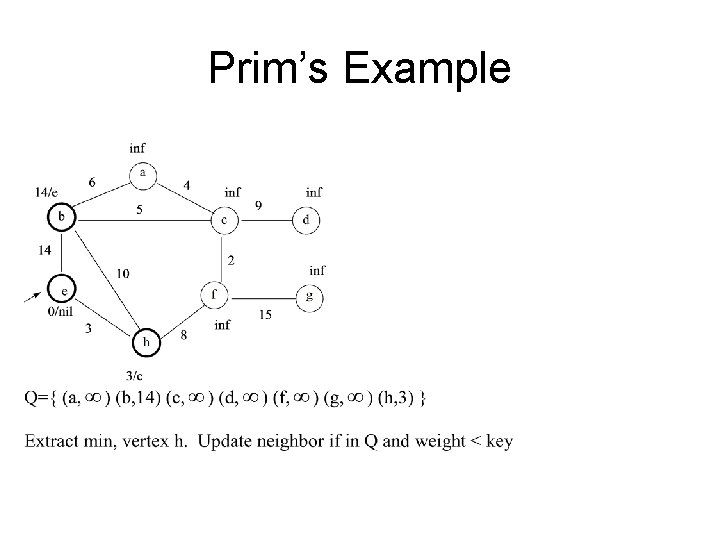
Prim’s Example

Prim’s Example

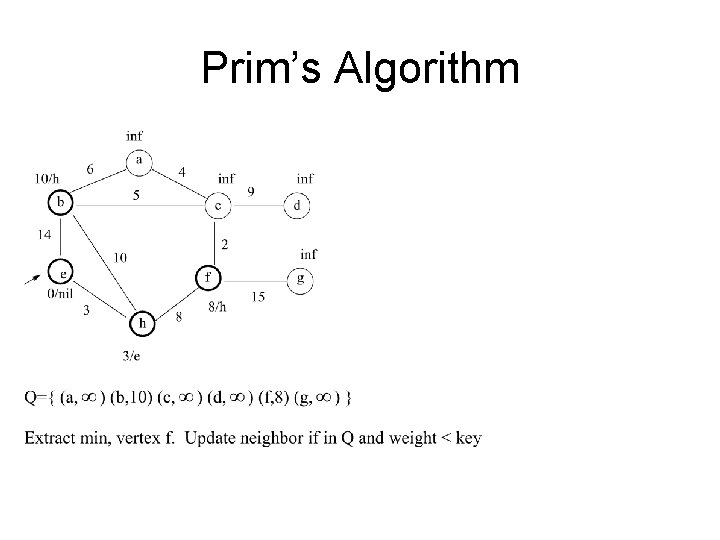
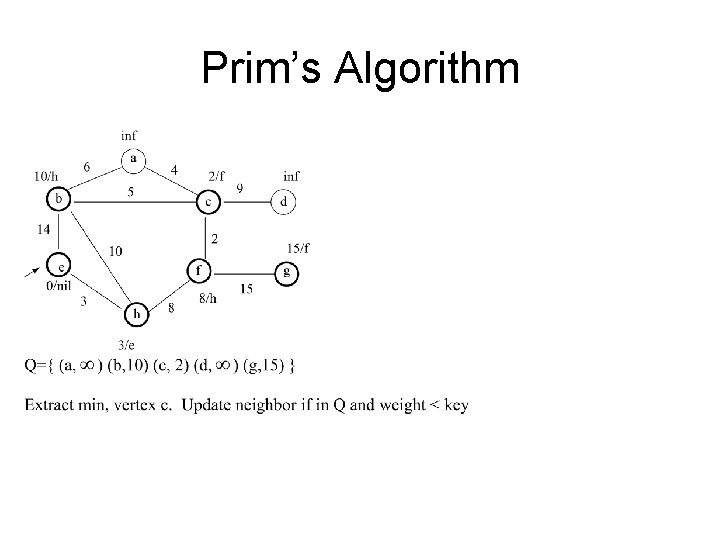
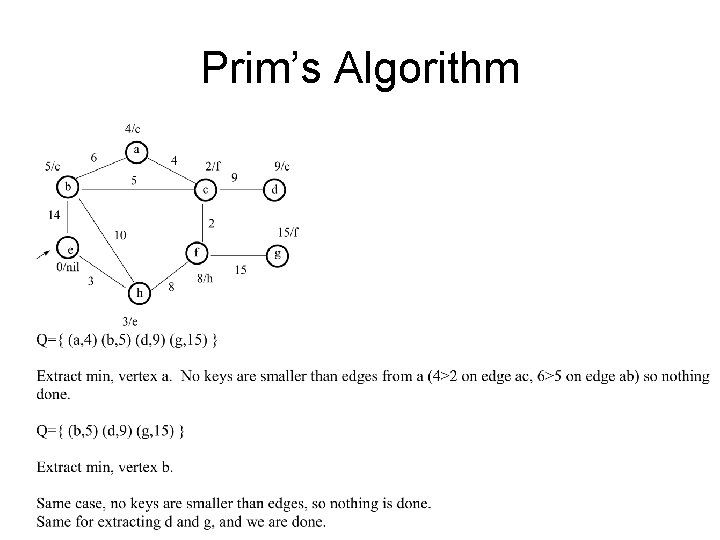
Prim’s Algorithm

Prim’s Algorithm

Prim’s Algorithm

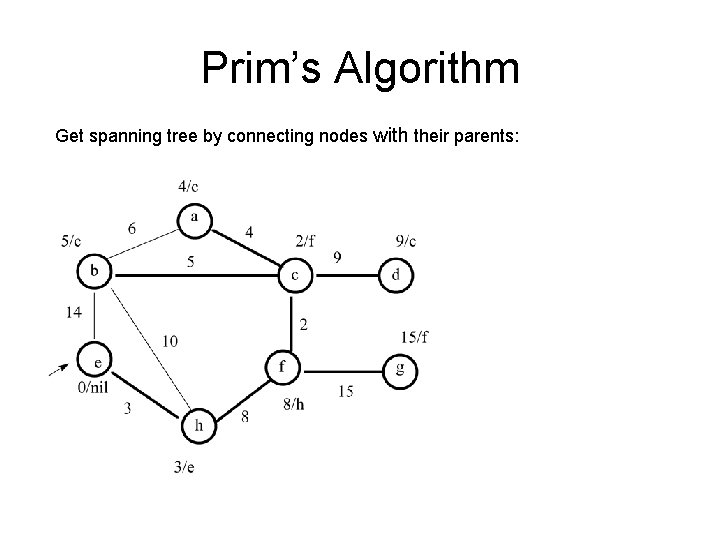
Prim’s Algorithm Get spanning tree by connecting nodes with their parents:

Runtime for Prim’s Algorithm MST-Prim(G, w, r) ; Graph G, weights w, root r Q ¬ V[G] for each vertex u ÎQ do key[u] ¬ ¥ ; infinite “distance” key[r] ¬ 0 P[r] ¬ NIL while Q is not empty do u ¬ Extract-Min(Q) ; remove closest node ; Update children of u so they have a parent and a min key val ; the key is the weight bet ween node and parent for each v Î Adj[u] do if v ÎQ & w(u, v)<key[v] then P[v] ¬ u key[v] ¬ w(u, v) O(V) if using a heap O(lg. V) if using a heap O(E) over entire while(Q not empty) O(lg. V) to update if using a heap! The inner loop takes O(E lg V) for the heap update inside the O(E) loop. This is over all executions, so it is not multiplied by O(V) for the while loop (this is included in the O(E) runtime through all edges. The Extract-Min requires O(V lg V) time. O(lg V) for the Extract-Min and O(V) for the while loop. Total runtime is then O(V lg V) + O(E lg V) which is O(E lg V) in a connected graph (a connected graph will always have at least V-1 edges).

Shortest Path Algorithms

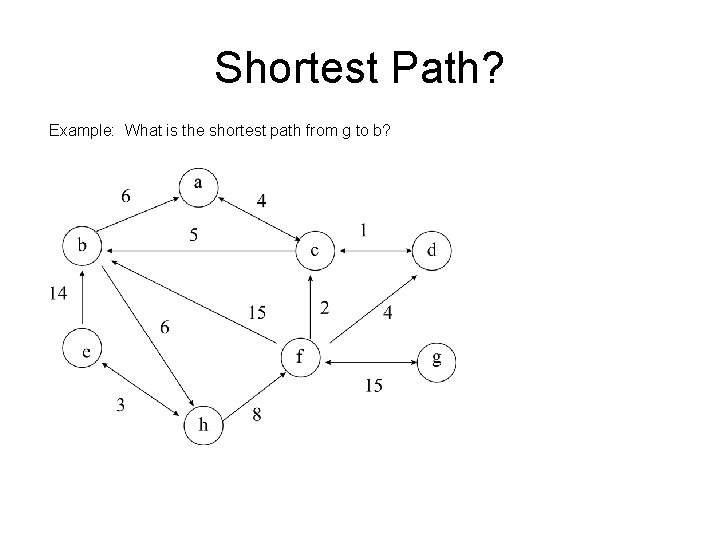
Shortest Path? Example: What is the shortest path from g to b?

Definitions • Formal definition of problem – Input: Weighted directed graph G=(V, E) plus w: E R, the weight function that maps from edges to weight values (real numbers). – Output: The shortest path between any source S and all other vertices. – The weight of a path is the sum of the weights of the edges on the path. • w(u, v) is the weight of arc that connects vertex u and v; it is not necessarily the min. • w(p) is the weight of some path p, where p is a list of vertices indicating the path from a source to destination. • (u, v) is the weight of the shortest path that connects vertex u and v.

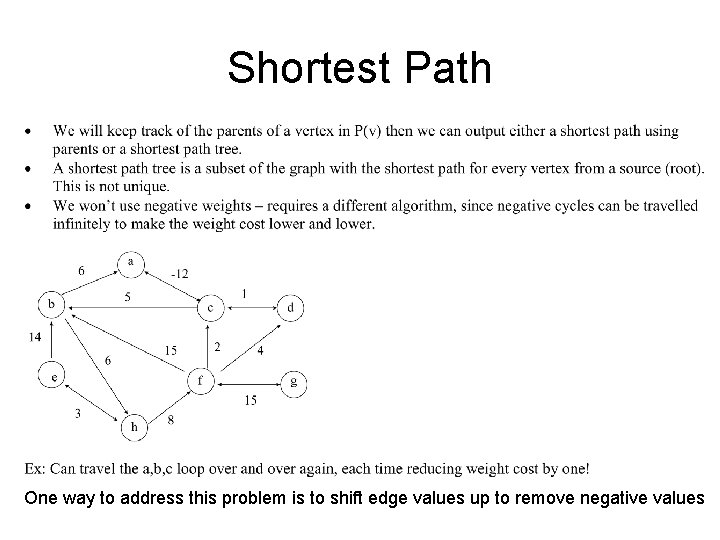
Shortest Path One way to address this problem is to shift edge values up to remove negative values

Properties of Shortest Paths

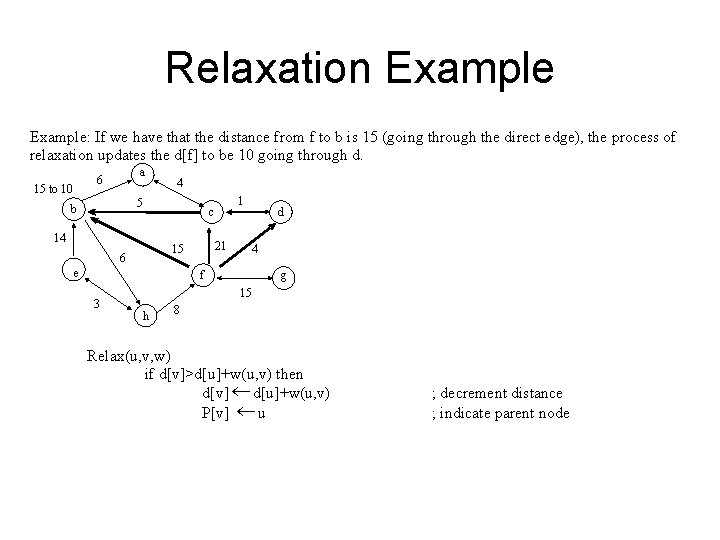
Relaxation Example: If we have that the distance from f to b is 15 (going through the direct edge), the process of relaxation updates the d[f] to be 10 going through d. a 6 15 to 10 4 5 b 14 21 15 6 1 c e d 4 f 3 g 15 h 8 Relax(u, v, w) if d[v]>d[u]+w(u, v) then d[v] ¬ d[u]+w(u, v) P[v] ¬ u ; decrement distance ; indicate parent node

Dijkstra’s Algorithm

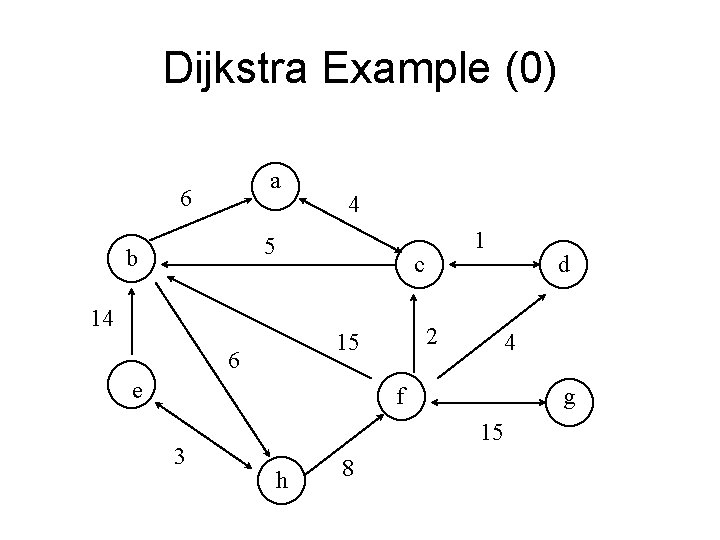
Dijkstra Example (0) a 6 4 5 b 1 c 14 2 15 6 e d 4 f 3 g 15 h 8

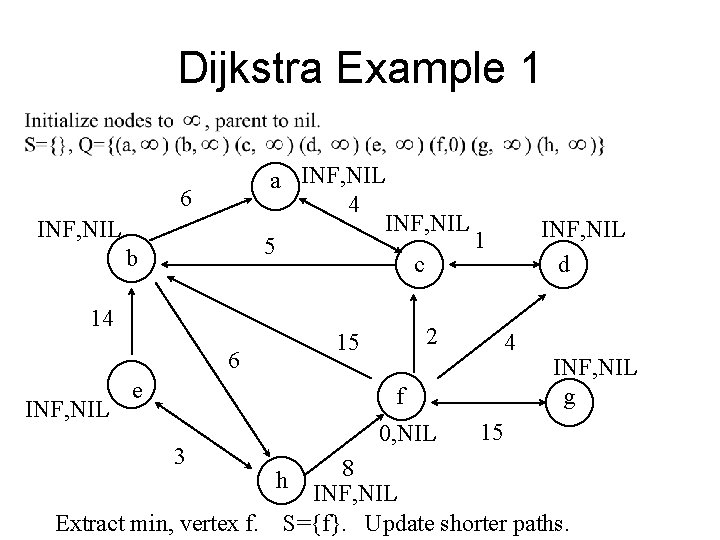
Dijkstra Example 1 a INF, NIL 4 INF, NIL 1 5 c 6 INF, NIL b 14 15 6 INF, NIL 2 e INF, NIL d 4 f 3 Extract min, vertex f. 0, NIL INF, NIL g 15 8 INF, NIL S={f}. Update shorter paths. h

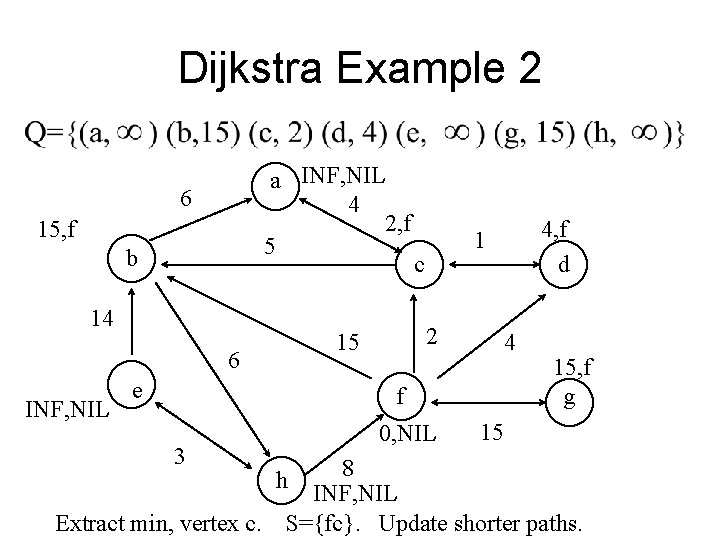
Dijkstra Example 2 a INF, NIL 4 2, f 5 6 15, f b 14 INF, NIL e c 2 15 6 4, f d 1 4 f 3 Extract min, vertex c. 0, NIL 15, f g 15 8 INF, NIL S={fc}. Update shorter paths. h

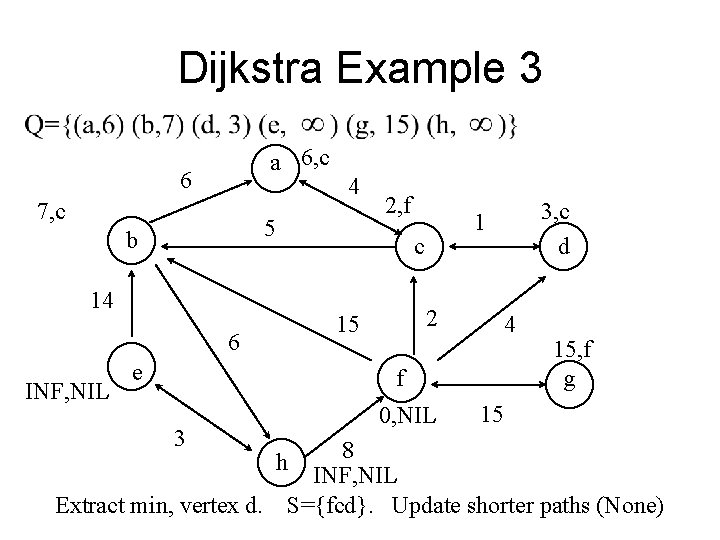
Dijkstra Example 3 a 6, c 6 7, c 5 b 2, f 2 15 6 e 3, c d 1 c 14 INF, NIL 4 4 f 3 Extract min, vertex d. 0, NIL 15, f g 15 8 INF, NIL S={fcd}. Update shorter paths (None) h

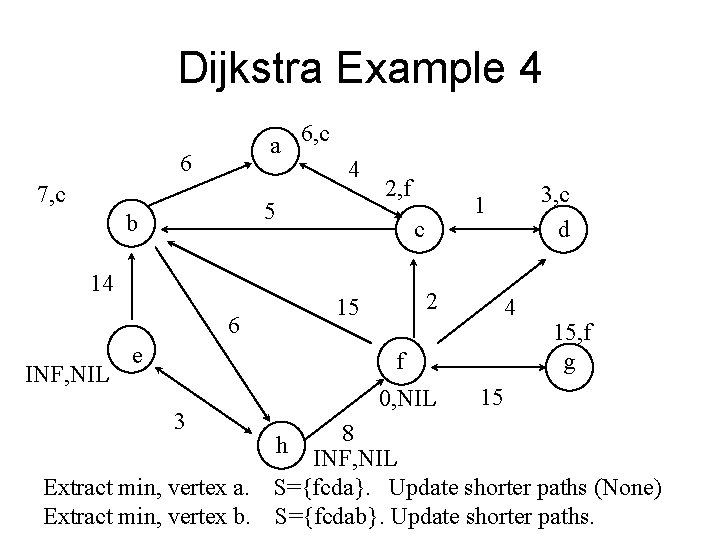
Dijkstra Example 4 a 6, c 6 7, c 5 b 2, f 2 15 6 e 3, c d 1 c 14 INF, NIL 4 4 f 3 0, NIL 15, f g 15 8 INF, NIL Extract min, vertex a. S={fcda}. Update shorter paths (None) Extract min, vertex b. S={fcdab}. Update shorter paths. h

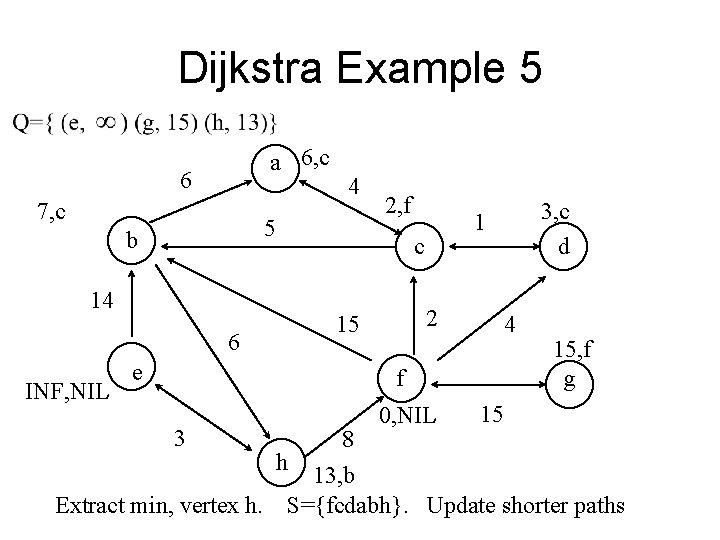
Dijkstra Example 5 a 6, c 6 7, c 5 b 2, f 2 15 6 e 3, c d 1 c 14 INF, NIL 4 4 f 3 Extract min, vertex h. h 8 0, NIL 15, f g 15 13, b S={fcdabh}. Update shorter paths

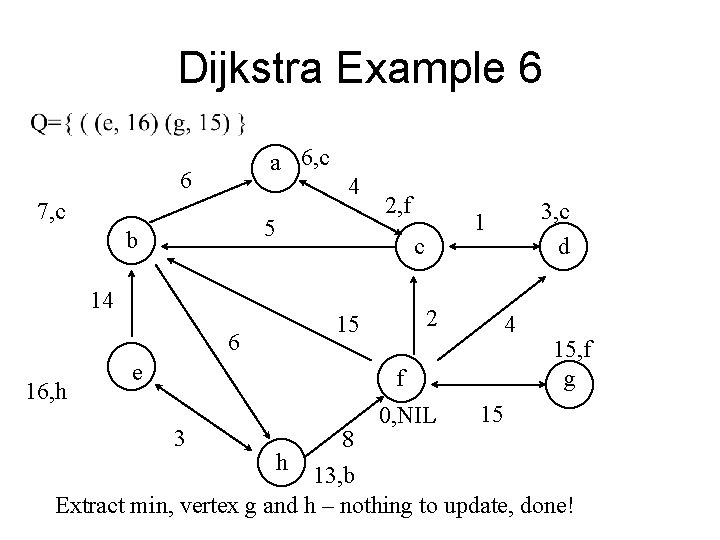
Dijkstra Example 6 a 6, c 6 7, c 5 b 2, f 2 15 6 e 3, c d 1 c 14 16, h 4 4 f 3 h 8 0, NIL 15, f g 15 13, b Extract min, vertex g and h – nothing to update, done!

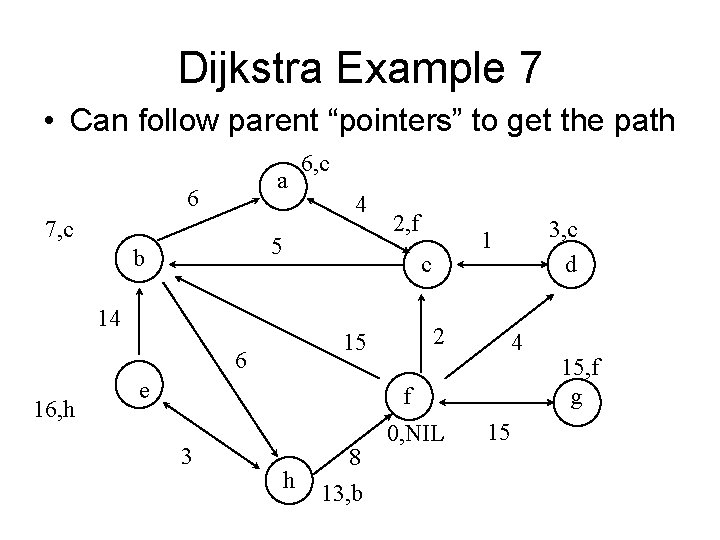
Dijkstra Example 7 • Can follow parent “pointers” to get the path a 6 7, c 4 5 b 2, f 2 15 6 e 3, c d 1 c 14 16, h 6, c 4 f 3 h 8 13, b 0, NIL 15 15, f g

Dijkstra vs. Prim’s MST • Very similar to Prim’s MST algorithm, but the two compute different things. Not the shortest path in MST, but picks shortest edge overall to connect all edges – (what case would the MST pick a different edge than Dijkstra? )

Dijkstra’s Runtime • Using a linear array for the queue, with the index as the vertex number, contents of array as its distance value O(V) to scan through array O(V) O(E) over entire while loop O(1) - direct access via array index Total runtime = O(V) + O(V 2) + O(E) = O(V 2)

Dijkstra’s Runtime • Using a min heap for the queue O(V) O(lg. V) O(E) over entire while loop O(lg. V) - must update heap key Total runtime = O(V) + O(Vlg. V) + O(Elg. V) = O(Elg. V) in a connected graph What if the graph is fully connected? O(V 2 lg. V) Actually slower than the simple array-based queue for dense graphs!

All Pairs Shortest Path • Finding the shortest path between all pairs of vertices • One solution is to run Dijkstra’s Algorithm for every vertex. This will require time O(V)(Time-Dijkstra). – If using a linear array for Q, this is time O(V 3). – There are other ways to solve this problem using dynamic programming which are studied in CSCE A 351