More Algorithms 20080924 Lecture 6 b CMSC 104

More Algorithms 2008/09/24: Lecture 6 b CMSC 104, Section 0101 John Y. Park 1

More Algorithms Topics l l l Algorithms: Elements in Depth In-Class Project: Euclid’s Algorithm In-Class Project: Student Voluteerizer Reading l None 2

Pseudocode: Control Structures Any problem can be solved using only three logical control structures: l l l Sequence Selection Repetition 3

Sequence l l A series of steps or statements that are executed in the order they are written. Example: Display “Enter two numbers: “ Read <number 1> Read <number 2> <sum> = <number 1> + <number 2> Display “sum = “, <sum> 4

Sequence l Some languages… l l Have line numbers Allow a set of sequenced steps to be grouped as a “statement block” l l Explicitly bracketed (e. g. , with “begin…end” or {…} Allow “goto”s l Evil-evil!!!!! 5

Sequence l Goto e. g. : <a> = 0 goto Label 3: Label 1: DISPLAY “Hello” DISPLAY “bye” Label 2: <a> = <a> + 1 DISPLAY <a> goto Label 1: DISPLAY “Never get here…” Label 3: DISPLAY “Starting up” goto Label 2: 6

Sequence l You should try to avoid the “goto” like the plague! In this class, you will never need to use a “goto” DON’T USE GOTOs!!! l Why did I even mention it? l l l It is a vehicle for explaining what other control structures are doing, in a more logical manner 7

Selection l Defines one or more courses of action depending on the evaluation of a condition. l Synonyms: conditional, branching, decision l Examples: If (condition is true) do this End_if If (condition is true) do this Else do that End_if 8

Selection l More complex examples: § DISPLAY “Enter number to invert” READ <my_num> If (<my_num> < 0) DISPLAY “Don’t like negative numbers” if (<my_num> < -999) DISPLAY “… but I guess you really do!” End_if Else_if (<my_num> == 0) <result> = 0 Else <result> = 1 / <my_num> End_if 9

Repetition l Allows one or more statements to be repeated as long as a given condition is true. l Synonyms: looping, iteration l Example: While (condition is true) do this End_while 10

Repetition l More complex example (with mistakes) § DISPLAY “Enter number to compute factorial for” READ <my_num> While (<my_num> > 0) <factorial> = <factorial> * <my_num> = <my_num> - 1 End_while DISPLAY “The factorial of”, <my_num>, “ is “, <factorial> 11

Repetition l More complex example (with mistakes) § DISPLAY “Enter number to compute factorial for” READ <my_num> <factorial> = 0 While (<my_num> > 0) <factorial> = <factorial> * <my_num> = <my_num> - 1 End_while DISPLAY “The factorial of”, <my_num>, “ is “, <factorial> 12

Repetition l More complex example (with mistakes) § DISPLAY “Enter number to compute factorial for” READ <my_num> <factorial> = 0 <saved_my_num> = <my_num> While (<my_num> > 0) <factorial> = <factorial> * <my_num> = <my_num> - 1 End_while <my_num> = <saved_my_num> DISPLAY “The factorial of”, <my_num>, “ is “, <factorial> 13

Pseudocode Style l l l Any user prompts should appear exactly as you wish the programmer to code them. The destination of any output data should be stated, such as in “Display”, which implies the screen. Make the data items clear (e. g. , surround them by < and > ) and give them descriptive names. Use formulas wherever possible for clarity and brevity. Use keywords (such as Read and While) and use them consistently. Accent them in some manner. 14
![Pseudocode (con’t) [Review] l l Use indentation for clarity of logic. Avoid using code. Pseudocode (con’t) [Review] l l Use indentation for clarity of logic. Avoid using code.](http://slidetodoc.com/presentation_image_h2/11e6692b663c87365c4667fc3a10153c/image-15.jpg)
Pseudocode (con’t) [Review] l l Use indentation for clarity of logic. Avoid using code. Pseudocode should not be programming language-specific. Always keep in mind that you may not be the person translating your pseudocode into programming language code. It must, therefore, be unambiguous. You may make up your own pseudocode guidelines, but you MUST be consistent. 15

Euclid’s Algorithm Problem: Find the largest positive integer that divides evenly into two given positive integers (i. e. , the greatest common divisor). Algorithm: 1. 2. 3. Assign M and N the values of the larger and smaller of the two positive integers, respectively. Divide M by N and call the remainder R. If R is not 0, then assign M the value of N, assign N the value of R, and return to Step 2. Otherwise, the greatest common divisor is the value currently assigned to N. 16
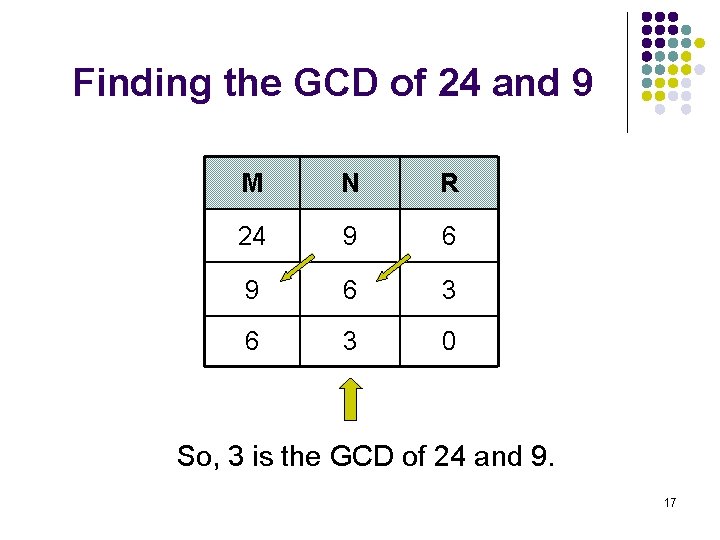
Finding the GCD of 24 and 9 M N R 24 9 6 3 6 3 0 So, 3 is the GCD of 24 and 9. 17

Euclid’s Algorithm Tips about problem # 1 : l The user should specify the two numbers to factor. She may enter them in any order (i. e. , don't assume first is greater). l You will need a new arithmetic operation for computing remainders: the '%' operator. E. g. : l "24 % 7" equals "3" l “-5 % 2” equals “-1”, and "18 % -8" equals "+2" l "7 % 0" equals "the end of the world as we know it. " The user may input one or both values as negative numbers. You must either: l l explicitly test for and reject negative numbers l make sure your algorithm computes the correct answer with them 18

Student Voluteerizer Problem: Write a generic algorithm for helping call on student “volunteers” in a “fair” manner <obviously underspecified…> 19
- Slides: 19