Montgomery multiplication Algorithm Under supervision of Dr S

Montgomery multiplication Algorithm Under supervision of : Dr. S. Bayat-sarmadi Mohammad Farmani 2 nd. Semister, 1392 -93 Sharif University of Technology 1

Main Topic Ø Montgomery modular multiplication algorithm Main Article: “Montgomery Multiplication in GF(2 k)” Written by: Cetin K. KOC and Tolga Acar, 1998 Copyright © 2014 Hardware Security and Trust Sharif University of Technology 2

Montgomery multiplication algorithm Outline n Introduction n Montgomery modular multiplication of integers n Montgomery modular multiplication in GF(2 k) n Conclusion Copyright © 2014 Hardware Security and Trust Sharif University of Technology 3

Montgomery multiplication algorithm Introduction • The importance and applications of the arithmetic operations in the Galois field GF(2 k) in : • • Coding theory Computer algebra Cryptography …. • Importance of the exponentiation • Using a series of multiplication for The exponentiation Copyright © 2014 Hardware Security and Trust Sharif University of Technology 4

Montgomery multiplication algorithm Introduction • Cryptographic applications require fast arithmetic operations • Proposed an effective modular multiplication of integers by P. L. Montgomery 1985 • Conversion to the Montgomery domain : an intger M : modulus r : Radix Copyright © 2014 Hardware Security and Trust Sharif University of Technology 5

Montgomery multiplication algorithm Introduction • Example: M = 11 , r = 24 = 16 • There is a one-to-one correspondence between integers and Montgomery residues for 0 < a < M-1 Copyright © 2014 Hardware Security and Trust Sharif University of Technology 6

Montgomery multiplication algorithm Outline n Introduction n Montgomery modular multiplication of integers n Montgomery modular multiplication in GF(2 k) n Conclusion Copyright © 2014 Hardware Security and Trust Sharif University of Technology 7

Montgomery multiplication algorithm Montgomery multiplication of Integers • Define: • r-1 is the inverse of r mod M: • r-1 r = 1 (mod M) Copyright © 2014 Hardware Security and Trust Sharif University of Technology 8

Montgomery multiplication algorithm Montgomery multiplication of Integers • Example : Copyright © 2014 Hardware Security and Trust Sharif University of Technology 9

Montgomery multiplication algorithm Montgomery multiplication of Integers • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 10

Montgomery multiplication algorithm Montgomery multiplication of Integers • Example : • X = 7 = 0111 • Y = 5 = 0101 • M = 11 = 1011 • • • Z initially 0 Z = (0 + 5 + 11) / 2 = 8 Z = (8 + 5 + 11) / 2 = 12 Z = (12 + 5 + 11) / 2 = 14 Z = (14 + 0) / 2 = 7 (final result) Copyright © 2014 Hardware Security and Trust Z = 0 for i = 0 to n-1 Z = Z + xi • Y if Z is odd then Z = Z + M Z = Z/2 if Z ≥ M then Z = Z – M Sharif University of Technology 11

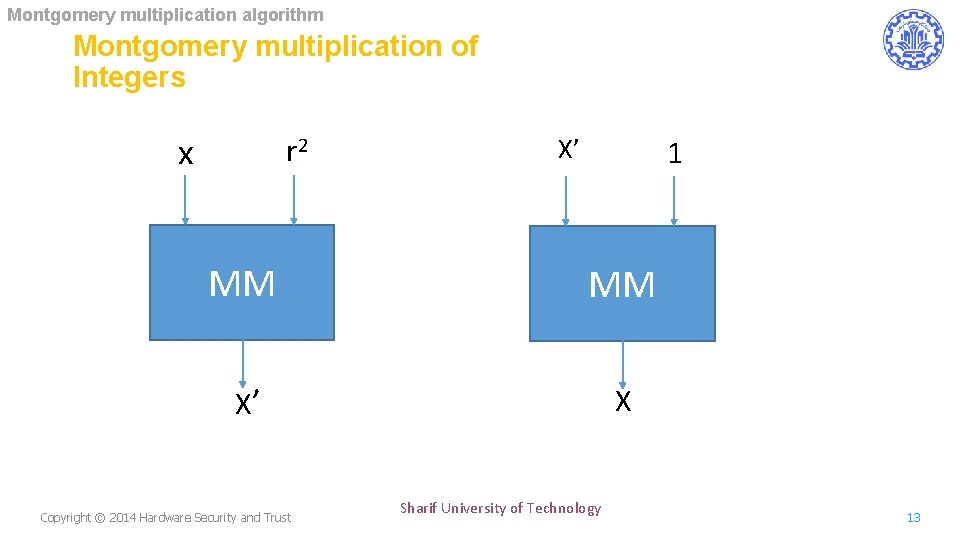
Montgomery multiplication algorithm Montgomery multiplication of Integers • Conversion using MM Conversion of integers to/from Montgomery residues with one MM operation Copyright © 2014 Hardware Security and Trust Sharif University of Technology 12

Montgomery multiplication algorithm Montgomery multiplication of Integers x r 2 X’ 1 MM MM X’ X Copyright © 2014 Hardware Security and Trust Sharif University of Technology 13

Montgomery multiplication algorithm Outline n Introduction n Montgomery modular multiplication of integers n Montgomery modular multiplication in GF(2 k) n Conclusion Copyright © 2014 Hardware Security and Trust Sharif University of Technology 14

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 15

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 16

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 17

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 18

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 19

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 20

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 21

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 22

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 23

Montgomery multiplication algorithm Montgomery multiplication in GF(2 k) • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 24

Montgomery multiplication algorithm Outline n Introduction n Montgomery modular multiplication of integers n Montgomery modular multiplication in GF(2 k) n Conclusion Copyright © 2014 Hardware Security and Trust Sharif University of Technology 25

Montgomery multiplication algorithm Conclusion • Copyright © 2014 Hardware Security and Trust Sharif University of Technology 26

End of presentation, Any question?