Monte Carlo Monte Carlo studies are one of

Monte Carlo

Monte Carlo studies are one of the earliest computer techniques, dating back to the 1940’s, they allow us to analyse a range of questions which are not directly tractable to an analytical solution. Sometimes these problems may be simply so complex that we can not work out the large sample (asymptotic)answer. In other cases we may be interested in the answer for a small sample size or a limited number of states which are not easily calculated. This technique has an enormous range of applications, pure statistics, project appraisal, macroeconomic models, derivative pricing – almost anywhere there are either stochastic

The essence of the technique is to assume a known world (DGP), to assume something about the statistical distribution of certai events. Then to numerically draw manyrealisationsfrom this distribution. Calculate the outcome andanalyse the resulting distribution of solutions.

A simple example from Metropolis and. Ulam Suppose we wish to evaluate the relative volume of a region in 20 dimensional space where the region is defined by 20 non linear inequalities as follows, Where we define the xs to lie in a unit cube.

In effect we are asking what is the proportion of points in this space which lie inside these inequalities. For some simple functionsit may be possible using integration to solve this analytically but generally this will not be possible. We could think of dividing up the unit interval into say 10 sections for each x and then checking each point this would lead to checking 100, 000, 000 different points.

The monte carlo approach would take the above set of equations as the DGP, assume the xs are generated by an independent uniform distribution over the unit interval. It would then generate say 5000 random draws from this distribution. It would then calculate what proportion of these draws are in th area defined above. This would then be an approximation to the size of the area.

A Statistical Example If we have a symmetric distribution such as the normal or `t’, w know that the mean and the median should be identical in term of their asymptotic properties. But what about in a small sample? Intuitively if the sample is very small we might expect the mean to do badly because any outlier will be given too much weight. In a bigger sample the mean may be a better. But where is the divide, and is this true.

A Monte Carlo Draw a set of n observations from a `t’ distribution with d degrees of freedom. Calculate the mean and the median. Repeat this R times. Tabulate the relative error ratio of the median to the mean

d=3 d=6 d=10 n=10 0. 29 0. 91 1. 03 n=25 0. 89 0. 93 1. 08 n=100 1. 19 1. 34 So the median does best for n<=25 and d<=6

Project Appraisal We can evaluate the likely profitabilityof a project using these techniques in the light of many uncertainties using this technique. Build a model of the cash flow of the project which calculates the net present value as an output.

Draw random realisations of the uncertain factors which might affect the project. Repeat many simulations. Calculate the distribution of the net present value. This gives the probabilityof making a profit and a standard error around this. So we can asses how uncertain we are about this mean forecast. We can also asses the probability of making a loss of a particular size.

Generating random numbers In fact all computer generated random numbers come from a fixed deterministicsequence which is highly non-linear so that the numbers appear random. They are therefore called pseudorandom numbers. Most computers start with a uniform random number over the interval 0 -1, and then transform this to derive particular distributions. Because the numbers are generated from a formulae the set of numbers depends on an initial value which starts of the whole sequence. This is called the seed.

GAUSS will normally take the system time as the seed value, this is pretty much a random event. Sometimes it is useful to produce identical sequences of random numbers then we can set the seed to an actual value. This is done with this command rndseed= 1000; or any other fixed number Generating Random Numbers in GAUSS

Having either defined a seed or used the default of the system clock to seed the process we can then generate a series of uniform random numbers by, y=rndu(r, c); where r is the number of rows And c the number of columns So y=rndu(5, 1); would create a column of 5 uniform random numbers

similarly normal (0, 1) random numbers are generated by, y=rndn(r, c); we can then transform these as we want, so if we want a set of 50 normal numbers with mean 10 and variance 25 (standard error 5), x=10+y*5; y=rndn(50, 1); Other distributions can be created by transforming these random numbers (see. Hendry article).

Increasing efficiency There a range of tricks which allow us to increase the efficiency of amonte carlo. Antithetic. Variates If we are interested in estimating the mean of a process then this trick can increase the efficiency of the monte carlo enormously. The idea is that we perform the simulations in pairs, the second one of the pair uses the same absolute values for the random shocks but with the opposite sign. This guarantees that we are always using an exactly symmetric distribution.

Control Variates This is a technique which is problem specific but it really amounts to using our knowledge of the structureof the problem to increase the efficiency of the replications. This will generally involve adding restrictions on the way the model works to ensure that it exactly follows our prior beliefs in some way. See the Boyle et al paper.

So to generate antithetic values for z. y=rndn(50, 1); x=10+y*5; i=1; do while i<=2; if i=1; z=x; elseif i>1; z=-x; endif; i=i+1; endo; Note this does not help if we are interested in assessing the variance of an outcome.

Moment Matching This is a generalisation of antithetics. The idea is that we transform the random numbers in each replication to exactly match some of the moments of the underlying distribution. So to exactly match the zero mean assumption. y=rndn(50, 1); a=meanc(y); b=stdc(y); z=(y-a)*(1/b); x=10+z*5; There also a range of morespecialised techniques surveyed in Boyle.

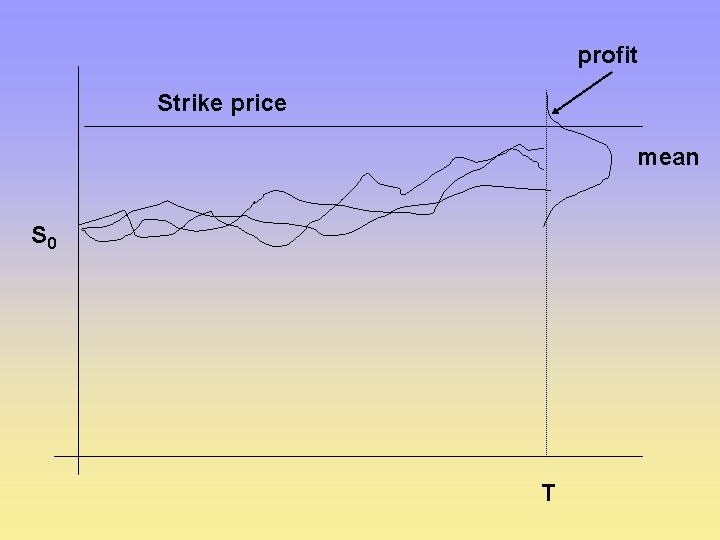
Option Pricing through Monte Carlo. In the case of a standard European call option we can use Black-Scholes, but we can illustrate themonte carlo approach to get the same answer. If S 0 is the current stock price, r is the risklessrate of return, I is the conditional variance of the stock, T is the maturity date and z are independent standard normal random numbers. Then for a particular realisation of z the price at T is,

So the price of the option with strike K will be given by This can be approximated in amonte carlo by

profit Strike price mean S 0 T

and if we assumed some other process to generate TS, or a variable strike price or a different distribution of shocks etc. we can still perform the simulation.

** MONTE 3. JOB ** A MONTE CARLO SIMULATION ** for derivative pricing withantithetics period =50; reps=500; tau=5/12; reps 2=reps*2; i=1; m=0; cls; print "replications = " reps; print "Number of periods per year ahead = " period; print "proportion of a year for durationtau)= ( " tau; nobs=trunc(period*tau);

@calcualte period standard error tocompund up to 0. 15@ c = { 0 }; c[1]=( (0. 15^2)/period)^0. 5; print "Standard error of returns"; print c[1]; x=zeros(1, reps 2); y=zeros(1, reps 2); z=zeros(1, reps 2); w=zeros(1, reps 2); p=zeros(nobs, 1); rndseed 23456567; p[1, 1]=62; strike=60; @calculates period rate from ananual rate of 10% @ r=(1+0. 10)^(1/period)-1;

do while i<=reps; e = rndn(nobs, 1); @ GENERATE NORMAL ERRORS @ j=1; do while j<=2; This simulates the path of if j <= 1; the asset price k=1; do while k<nobs; k=k+1; p[k, 1]=exp( ln(p[k-1, 1]) + r +e[k]*c[1] ); endo; else; k=1; do while k<nobs; k=k+1; p[k, 1]=exp(ln(p[k-1, 1]) + r - e[k]*c[1] ); endo; endif ;

if p[nobs, 1]>strike; callprof=p[nobs, 1]-strike; putprof=0; else; callprof=0; putprof=strike-p[nobs, 1]; endif; m=m+1; x[1, m]=callprof; y[1, m]=putprof; z[1, m]=p[nobs, 1]; j=j+1; endo; i=i+1; endo; This decides if the put or call is in profit and collects up the profit values

m=meanc(z'); se=stdc(z'); m=meanc(x'); se=stdc(x'); cp=m[1, 1]*(1/(1+r))^nobs; print "call price = " cp; n=meanc(y'); se=stdc(y'); pp=n[1, 1]*(1/(1+r))^nobs; print "put price = " pp; end; Takes the mean of all the call profits, discounts it back to today, thats the call price Takes the mean of all the put profits, discounts it back to today and that’s the put price