Monte Carlo Monte Carlo Goal Evaluate an integral

第九章 Monte Carlo积分

第九章 Monte Carlo积分 Goal: Evaluate an integral: Why use random methods? Computation by “deterministic quadrature” can become expensive and inaccurate. v grid points add up quickly in high dimensions v bad choices of grid may misrepresent g(x)

第九章 Monte Carlo积分 q Monte Carlo method can be used to compute integral of any dimension d (d-fold integrals) q. Error comparison of d-fold integrals approximating the integral of a function f using quadratic polynomials Simpson’s rule, … Monte Carlo method purely statistical, not rely on the dimension ! Monte Carlo method WINS, when d >> 3

第九章 Monte Carlo积分 v. Hit-or-Miss Method v. Sample Mean Method v. Variance Reduction Technique v. Variance Reduction using Rejection Technique v. Importance Sampling Method

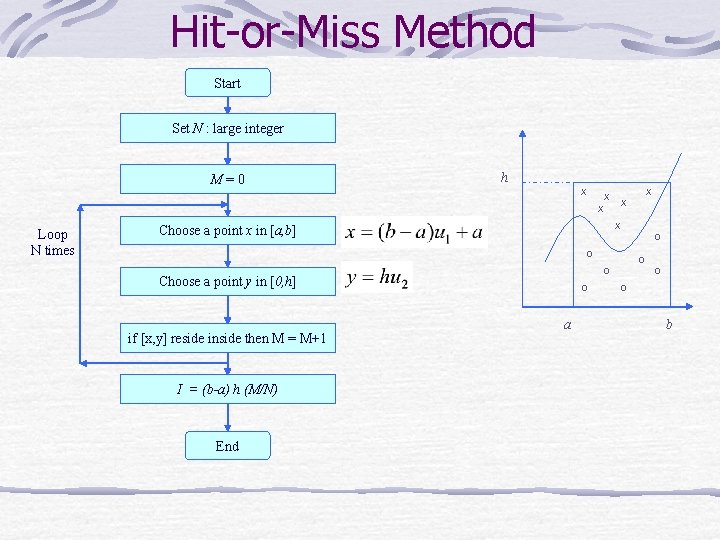
Hit-or-Miss Method • Evaluation of a definite integral h X X X O • Probability that a random point reside inside the area O O O a N : Total number of points M : points that reside inside the region b

Hit-or-Miss Method Sample uniformly from the rectangular region [a, b]x[0, h] The probability that we are below the curve is So, if we can estimate p, we can estimate I: where is our estimate of p

Hit-or-Miss Method We can easily estimate p: v throw N “uniform darts” at the rectangle v let M be the number of times you end up under the curve y=g(x) v let

Hit-or-Miss Method Start Set N : large integer M=0 h X X X Loop N times X Choose a point x in [a, b] O O Choose a point y in [0, h] if [x, y] reside inside then M = M+1 I = (b-a) h (M/N) End O O O a O O b

Hit-or-Miss Method Error Analysis of the Hit-or-Miss Method It is important to know how accurate the result of simulations are note that M is binomial(M, p)

第九章 Monte Carlo积分 v. Hit-or-Miss Method v. Sample Mean Method v. Variance Reduction Technique v. Variance Reduction using Rejection Technique v. Importance Sampling Method

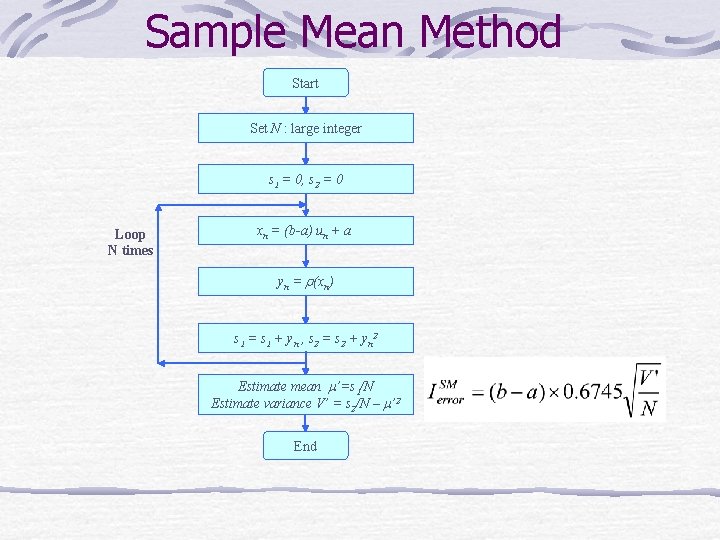
Sample Mean Method Start Set N : large integer s 1 = 0, s 2 = 0 Loop N times xn = (b-a) un + a yn = r(xn) s 1 = s 1 + y n , s 2 = s 2 + y n 2 Estimate mean m’=s 1/N Estimate variance V’ = s 2/N – m’ 2 End

Sample Mean Method Write this as: where X~unif(a, b)

Sample Mean Method where X~unif(a, b) So, we will estimate I by estimating E[g(X)] with where X 1, X 2, …, Xn is a random sample from the uniform(a, b) distribution.

Sample Mean Method Example: (we know that the answer is e 3 -1 19. 08554) v write this as where X~unif(0, 3)

Sample Mean Method v write this as where X~unif(0, 3) estimate this with where X 1, X 2, …, Xn are n independent unif(0, 3)’s.

Sample Mean Method Simulation Results: true = 19. 08554, n=100, 000 Simulation 1 19. 10724 2 19. 08260 3 18. 97227 4 19. 06814 5 19. 13261

Sample Mean Method Don’t ever give an estimate without a confidence interval! This estimator is “unbiased”:

Sample Mean Method

Sample Mean Method v an approximation

Sample Mean Method v X 1, X 2, …, Xn iid -> g(X 1), g(X 2), …, g(Xn) iid v Let Yi=g(Xi) for i=1, 2, …, n Then and we can once again invoke the CLT.

Sample Mean Method For n “large enough” (n>30), So, a confidence interval for I is roughly given by but since we don’t know , we’ll have to be content with the further approximation:

Sample Mean Method By the way… No one ever said that you have to use the uniform distribution Example: where X~exp(rate=2).

Sample Mean Method Comparison of Hit-and-Miss and Sample Mean Monte Carlo v Let be the hit-and-miss estimator of I v Let be the sample mean estimator of I Then

Sample Mean Method Comparison of Hit-and-Miss and Sample Mean Monte Carlo Sample mean Monte Carlo is generally preferred over Hitand-Miss Monte Carlo because: v the estimator from SMMC has lower variance v SMMC does not require a non-negative integrand (or adjustments) v H&M MC requires that you be able to put g(x) in a “box”, so you need to figure out the max value of g(x) over [a, b] and you need to be integrating over a finite integral.

2. 1 Variance Reduction Technique - Introduction

第九章 Monte Carlo积分 v. Hit-or-Miss Method v. Sample Mean Method v. Variance Reduction Technique v. Variance Reduction using Rejection Technique v. Importance Sampling Method

Variance Reduction Technique Introduction Monte Carlo Method and Sampling Distribution Monte Carlo Method : Take values from random sample From central limit theorem, 3 s rule Most probable error Important characteristics

Variance Reduction Technique Introduction Reducing error *100 samples reduces the error order of 10 Reducing variance Variance Reduction Technique The value of variance is closely related to how samples are taken Unbiased sampling Biased sampling More points are taken in important parts of the population

Variance Reduction Technique Motivation If we are using sample-mean Monte Carlo Method Variance depends very much on the behavior of r(x) varies little variance is small r(x) = const variance=0 Evaluation of a integral Near minimum points contribute less to the summation Near maximum points contribute more to the summation More points are sampled near the peak ”importance sampling strategy”

第九章 Monte Carlo积分 v 1. 2 Hit-or-Miss Method v 1. 3 Sample Mean Method v 2. 1 Variance Reduction Technique v 2. 3 Variance Reduction using Rejection Technique v 2. 4 Importance Sampling Method

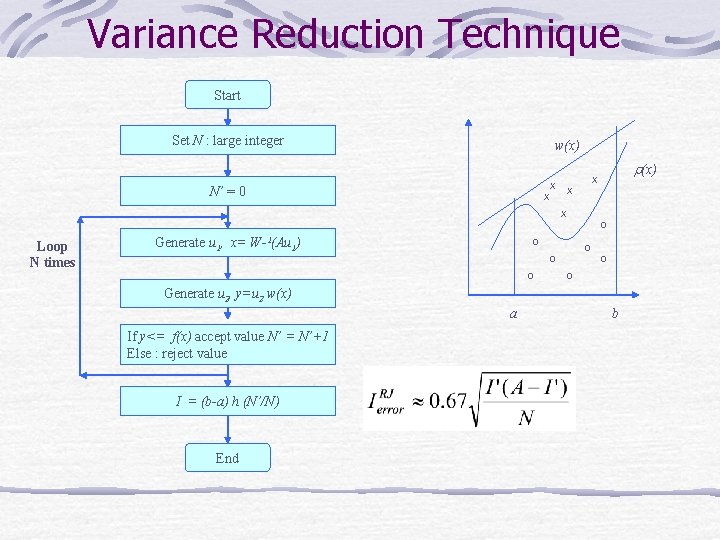
Variance Reduction Technique Variance Reduction for Hit-or-Miss method • In the domain [a, b] choose a comparison function w(x) X X r(x) X X X O O O a O O Points are generated on the area under w(x) function Random variable that follows distribution w(x) b

Variance Reduction Technique Points lying above r(x) is rejected w(x) X X r(x) X X X O O O q P(q) 1 r 0 1 -r a O O b

Variance Reduction Technique Error Analysis Hit or Miss method Error reduction

Variance Reduction Technique Start Set N : large integer w(x) X N’ = 0 r(x) X X O Loop N times Generate u 1, x= W-1(Au 1) O O O Generate u 2, y=u 2 w(x) a If y<= f(x) accept value N’ = N’+1 Else : reject value I = (b-a) h (N’/N) End b

第九章 Monte Carlo积分 v 1. 2 Hit-or-Miss Method v 1. 3 Sample Mean Method v 2. 1 Variance Reduction Technique v 2. 3 Variance Reduction using Rejection Technique v 2. 4 Importance Sampling Method

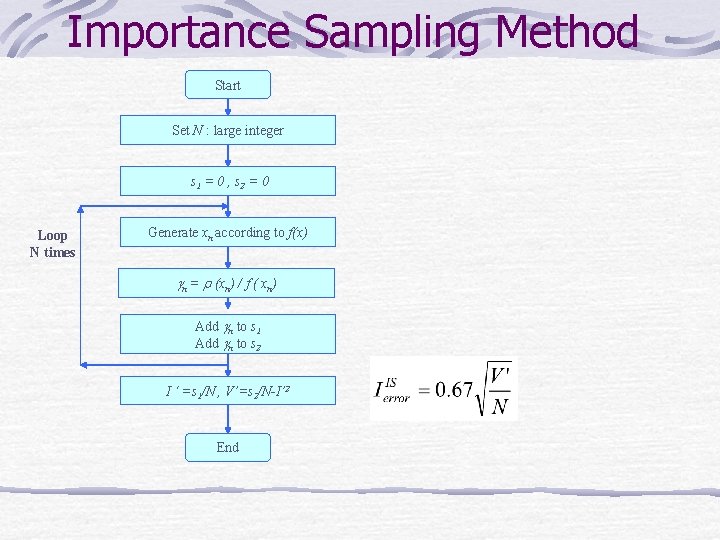
Importance Sampling Method Basic idea Put more points near maximum Put less points near minimum F(x) : transformation function (or weight function_

Importance Sampling Method if we choose f(x) = cr(x) , then variance will be small The magnitude of error depends on the choice of f(x)

Importance Sampling Method Estimate of error

Importance Sampling Method Start Set N : large integer s 1 = 0 , s 2 = 0 Loop N times Generate xn according to f(x) gn = r (xn) / f ( xn) Add gn to s 1 Add gn to s 2 I ‘ =s 1/N , V’=s 2/N-I’ 2 End