Monte Carlo Modeling of Photon Transport in Biological

Monte Carlo Modeling of Photon Transport in Biological Tissues Matija Milanic

Monte Carlo ?

Definition of Monte Carlo simulation “Monte Carlo simulation uses random sampling and statistical modeling to estimate mathematical functions and mimic the operations of complex systems. ” Robert L. Harrison, “Introduction To Monte Carlo Simulation, ” AIP Conf Proc. Jan 5, 2010; 1204: 17– 21.

Basic principle of Monte Carlo MC simulations follow this pattern: • model a system as a (series of) probability density functions (PDFs); • repeatedly sample from the PDFs; • tally/compute the statistics of interest.

History of MC • Simulation was first developed and used systematically during the Manhattan Project (WWII). • John von Neumann and Stanislaw Ulam suggested it to investigate properties of neutron travel through radiation shielding. • Being secret, the work of von Neumann and Ulam required a code name: Monte Carlo. • Parallel computing was done by rows and columns of mathematicians.

Human MC computer

MC today Today's applications of Monte Carlo methods include: • cancer therapy, • traffic flow, • Dow-Jones forecasting, • oil well exploration, • stellar evolution, • reactor design, • quantum chromo-dynamics … • modeling of materials and chemicals, • grain growth modeling in metallic alloys, • behavior of nanostructures and polymers, • protein structure predictions. … Photon transport in biological tissues.

Radiative Transfer Equation Divergence Extinction Scattering • RTE is difficult to solve. • Solution = diffusion approximation (DA) • DA – mua << mus Source

RTE vs. MC • RTE results = Monte Carlo results • RTE = analytical method • MC = numerical method ? ?

Definition of problem • Tissue geometry composed of laterally infinite layers. • Each layer: µa, µs, g, n, d. • Infinitely narrow photon beam – an impulse. • Physical quantities: • • Specific absorption A(r, z), Fluence F(r, z), Diffuse reflectance Rd(r, α), Transmittance Td(r, α). µa 1, µs 1, g 1, n 1 µa 2, µs 2, g 2, n 2 µa. N, µs. N, g. N, n. N

Definition of problem • Coordinate systems: • global Cartesian (x, y, z) – tracking photons, • global cylindrical (r, φ, z) – recording physical quantities, • local spherical (u, φ, ϑ) – scattering angles. • Grid representation for physical quantities.

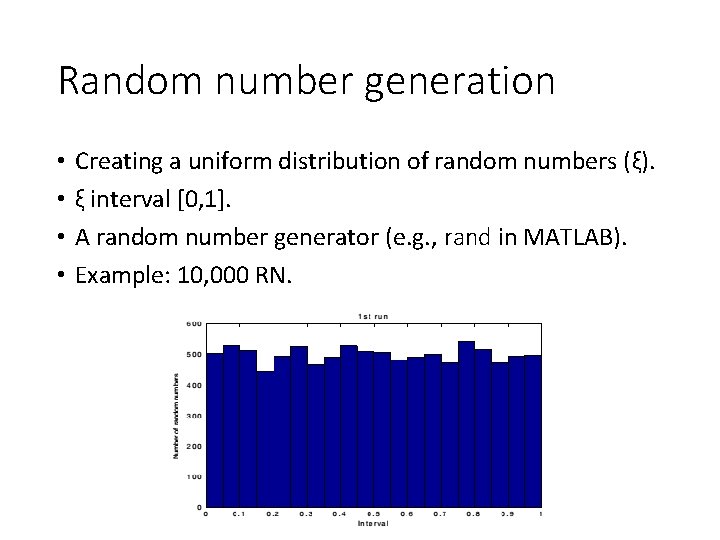
Random number generation • • Creating a uniform distribution of random numbers (ξ). ξ interval [0, 1]. A random number generator (e. g. , rand in MATLAB). Example: 10, 000 RN.

Sampling of a random variable • Probability density function p(χ): “is a function that describes the relative likelihood for this random variable to take on a given value” • Χ sampling equation: -log(ξ) • Inverse transformation: exp(-χ)

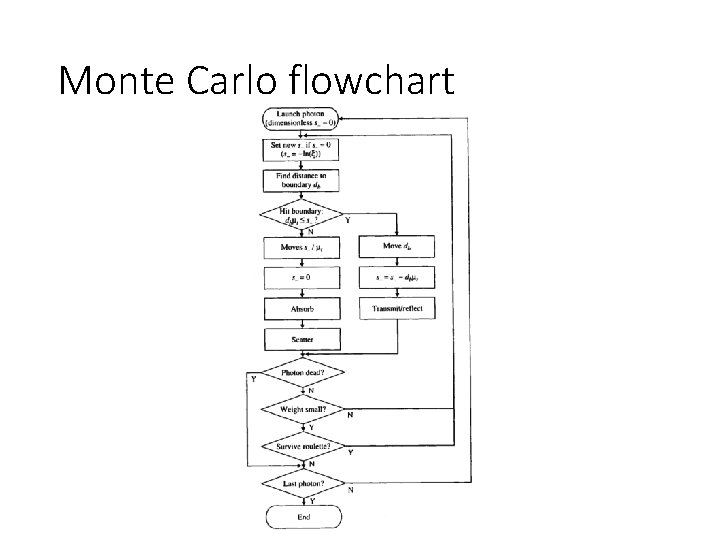
Monte Carlo flowchart

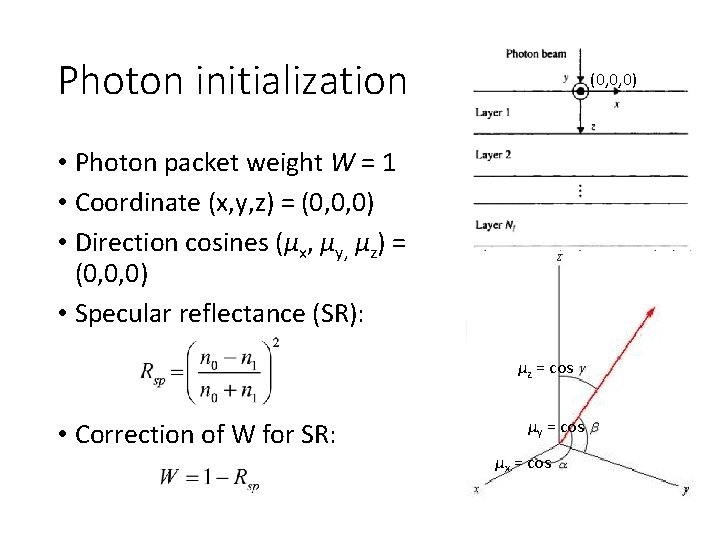
Photon initialization (0, 0, 0) • Photon packet weight W = 1 • Coordinate (x, y, z) = (0, 0, 0) • Direction cosines (μx, μy, μz) = (0, 0, 0) • Specular reflectance (SR): μz = cos • Correction of W for SR: μy = cos μx = cos

Step size of photon • Extinction coefficient: • Integral of d. P = interaction occurs outside [0, si) • Probability that interaction occurs within [0, si) • Step size

Distance to boundary • Find distance to boundary db • Hit boundary? W db si

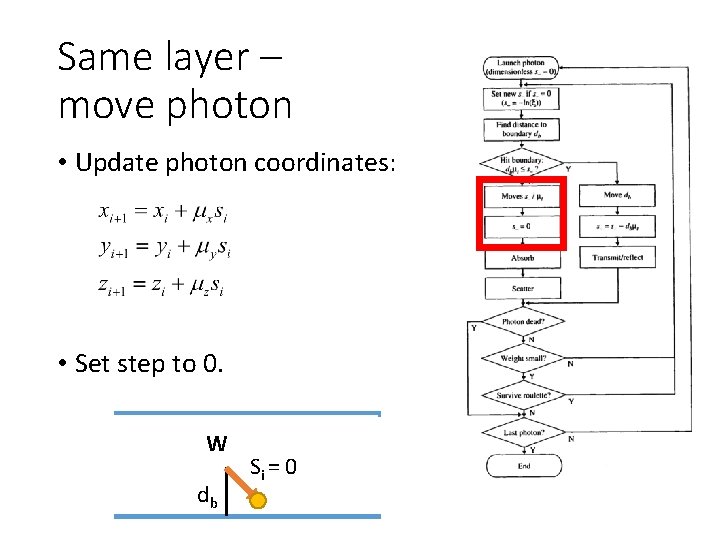
Same layer – move photon • Update photon coordinates: • Set step to 0. W db s. Sii = 0

Same layer absorbtion • Fraction energy absorbed: • Fraction recorded: • Weight updated: Wii+1

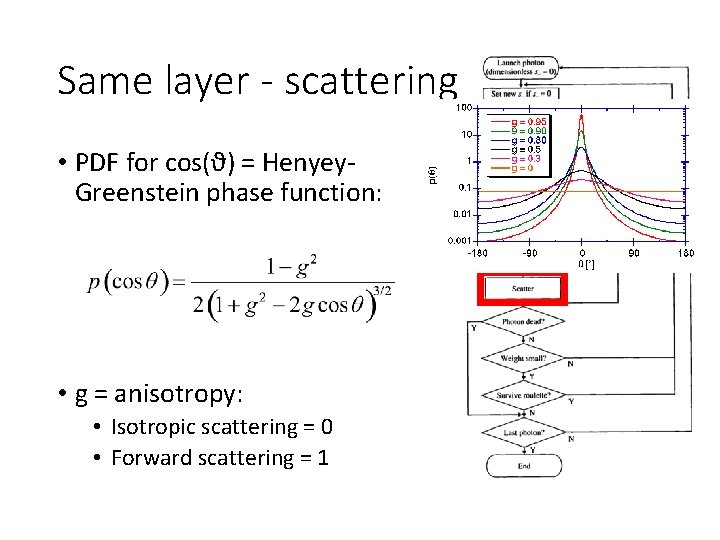
Same layer - scattering • PDF for cos(ϑ) = Henyey. Greenstein phase function: • g = anisotropy: • Isotropic scattering = 0 • Forward scattering = 1

Same layer - scattering • Cosine of polar angle - inverse P-1 of HG PDF: • Azimuthal angle – uniform distribution [0, 2π):

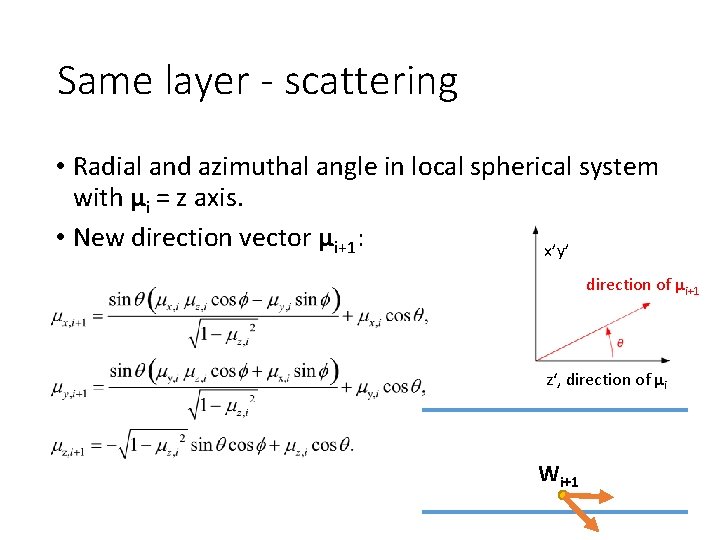
Same layer - scattering • Radial and azimuthal angle in local spherical system with μi = z axis. • New direction vector μi+1: x’y’ direction of μi+1 z‘, direction of μi Wi+1

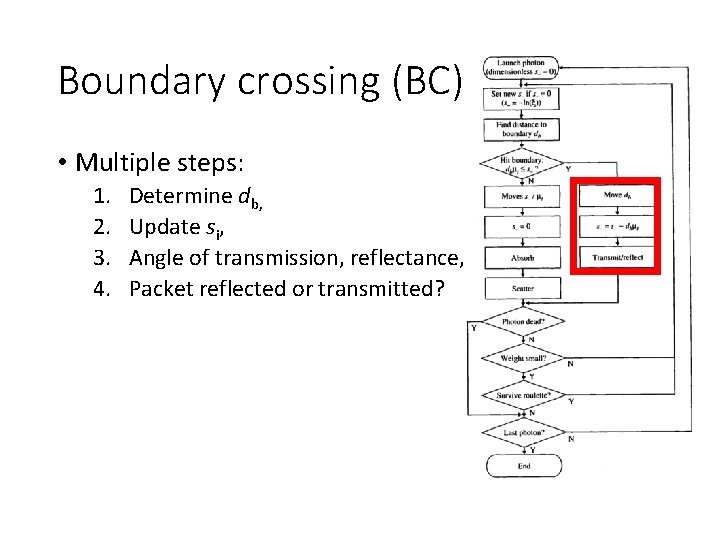
Boundary crossing (BC) • Multiple steps: 1. 2. 3. 4. Determine db, Update si, Angle of transmission, reflectance, Packet reflected or transmitted?

BC step 1 – determination of db z 0 W z 1 db si

BC step 2 – Update si • If db μt < si update si and move photon packet to boundary: z 0 W z 1 dbΔs si. W si

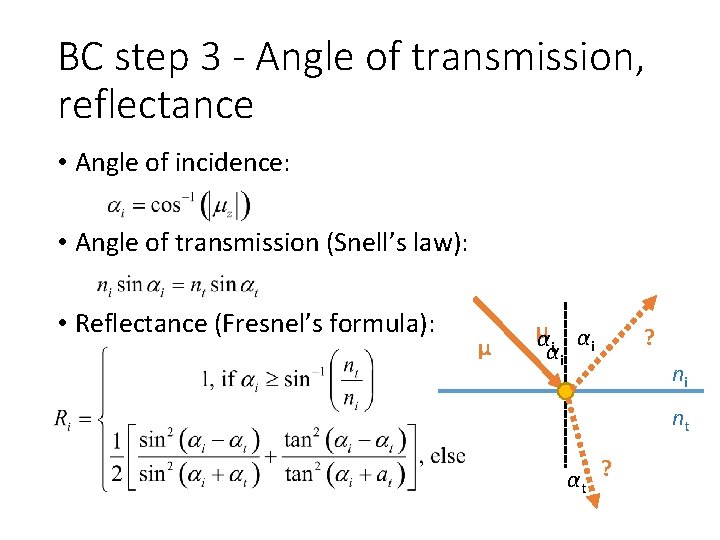
BC step 3 - Angle of transmission, reflectance • Angle of incidence: • Angle of transmission (Snell’s law): • Reflectance (Fresnel’s formula): μ μ αi αi αi ? ni nt αt ?

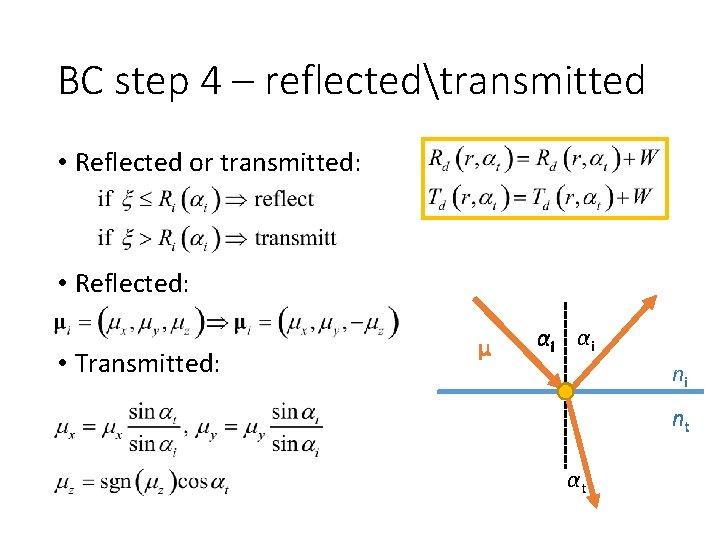
BC step 4 – reflectedtransmitted • Reflected or transmitted: • Reflected: • Transmitted: μ α i αi ni nt αt

Termination of packet • Reemission → photon dead • Small weight → Russian roulette:

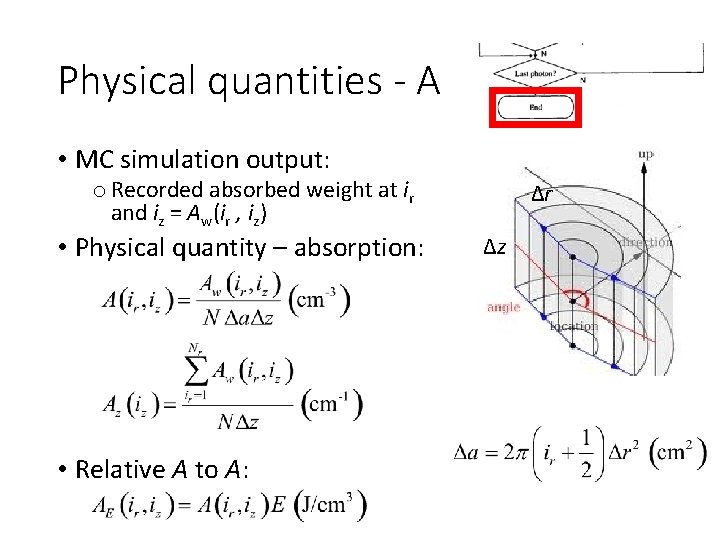
Physical quantities - A • MC simulation output: o Recorded absorbed weight at ir and iz = Aw(ir , iz) • Physical quantity – absorption: • Relative A to A: Δr Δz

Physical quantities - F • Energy fluence = energy flux integrated over time: Δr Δz

Physical quantities – Rd • MC simulation output: o Recorded remitted weight at ir and iα = Rd, w(ir , iα) • Physical quantity – diffuse reflectance:

Physical quantities – Td • MC simulation output: o Recorded remitted weight at ir and iα = Td, w(ir , iα) • Physical quantity – diffuse reflectance:

MCML – MC in multi-layered tissues • Wang L, Jacques SL, Zheng L. «MCML--Monte Carlo modeling of light transport in multi-layered tissues. » , Comput Methods Programs Biomed. 1995 Jul; 47(2): 131 -46. • Links: • http: //oilab. seas. wustl. edu/mc. html • http: //omlc. ogi. edu/software/mc/

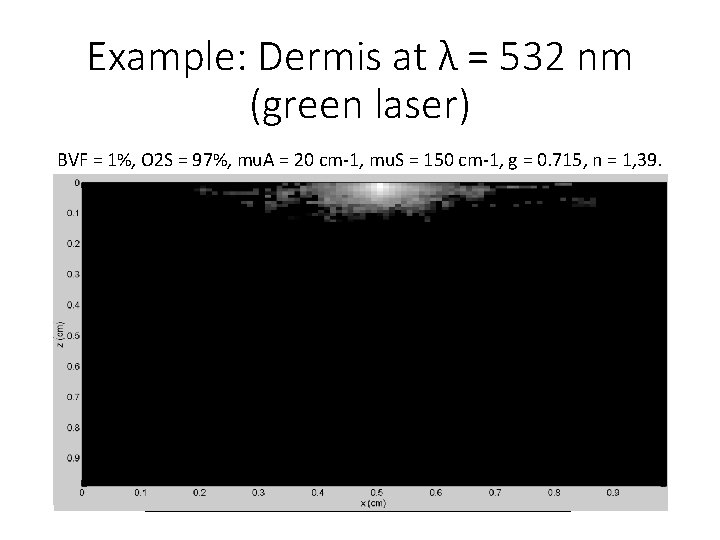
Example: Dermis at λ = 532 nm (green laser) BVF = 1%, O 2 S = 97%, mu. A = 20 cm-1, mu. S = 150 cm-1, g = 0. 715, n = 1, 39.

Example: Dermis at λ = 1064 nm (Nd: YAG laser) BVF = 1%, O 2 S = 97%, mu. A = 1 cm-1, mu. S = 60 cm-1, g = 0. 715, n = 1, 37.

Variants of MC • Geometry: • Layered planar (e. g. , MCML) • 3 D voxelized • 3 D mesh • Time: • Static (e. g. , MCML) • Dynamic • Speed: • Single CPU • Parallelized GPU • Physical phenomena: • Polarization • Fluoresecce …

Geometry - 3 D voxelized • Advantages: • Simulation of arbitrary geometry (e. g. , MRI) • Each voxel unique tissue properties • Weaknesses: • Computationally demanding • Inaccurate representation of smooth surfaces Majaron B et al, ” 3 D Monte Carlo model of optical transport in laser-irradiated cutaneous vascular malformations”, Proc. SPIE 7376

Geometry - 3 D mesh • Advantages: • Accurate representation of smooth surfaces • More optimal regarding computation • Weaknesses: • Complicated to generate appropriate mesh http: //mcx. sourceforge. net/cgi-bin/index. cgi? MMC

Time - Dynamic • MC can provide time evolution of photon transport • Temporally resolved imaging (e. g. , fluorescence imaging) http: //mcx. sourceforge. net/cgi-bin/index. cgi? MMC

Speed - Parallelization • CPU: • Using multiple cores on CPU • Speedup = 1 CPU time × number of cores • GPU: • CUDA algorithms (NVIDIA) • MCML for cuda (reported 600 x speedup) • 3 D MC for cuda (reported 75 x speedup) https: //code. google. com/p/gpumcml/ http: //mcx. sourceforge. net/cgi-bin/index. cgi

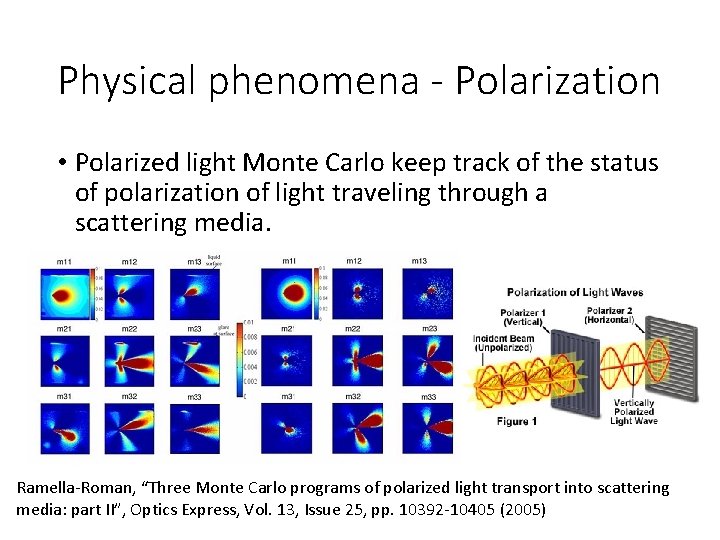
Physical phenomena - Polarization • Polarized light Monte Carlo keep track of the status of polarization of light traveling through a scattering media. Ramella-Roman, “Three Monte Carlo programs of polarized light transport into scattering media: part II”, Optics Express, Vol. 13, Issue 25, pp. 10392 -10405 (2005)

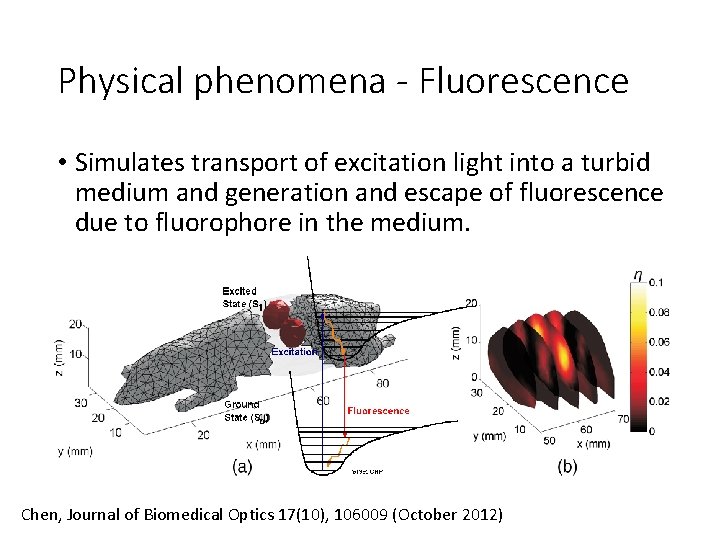
Physical phenomena - Fluorescence • Simulates transport of excitation light into a turbid medium and generation and escape of fluorescence due to fluorophore in the medium. Chen, Journal of Biomedical Optics 17(10), 106009 (October 2012)

Virtual Tissue Simulator http: //lammp. bli. uci. edu/software. php