Monte Carlo Methods CEE 6410 Water Resources Systems

Monte Carlo Methods CEE 6410 – Water Resources Systems Analysis Nov. 12, 2015

Learning Objectives 1. Monte Carlo simulate uncertain model parameters 2. Apply Monte Carlo simulations to • • Reservoir optimization problem (HW #7) Household water use in Amman, Jordan

1. Monte Carlo Simulation Statistical technique that quantifies the interactive effects of uncertainty, variation, and randomness of factors on a final product. e. g. , What net benefits does a reservoir generate with uncertain initial storage, inflows, and in-stream flow requirements?

Monte Carlo and Vegas!!!

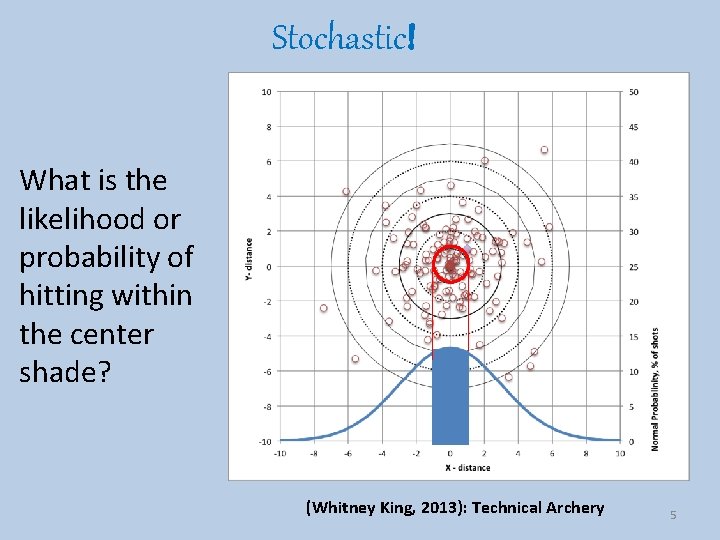
Stochastic! What is the likelihood or probability of hitting within the center shade? (Whitney King, 2013): Technical Archery 5

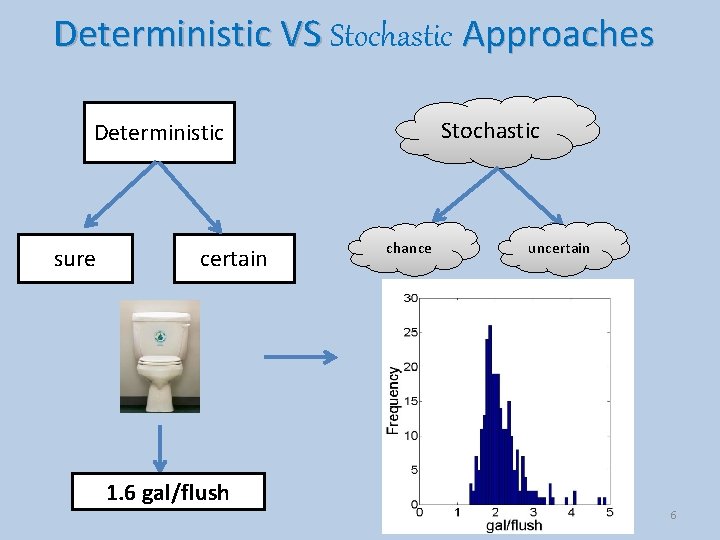
Deterministic VS Stochastic Approaches Stochastic Deterministic sure certain chance uncertain 1. 6 gal/flush 6

Probability Distributions By Raphael Briand

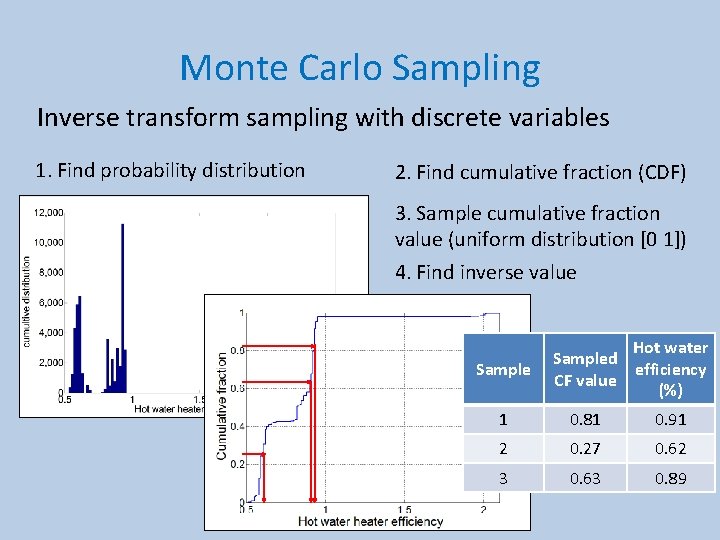
Monte Carlo Sampling Inverse transform sampling with discrete variables 1. Find probability distribution 2. Find cumulative fraction (CDF) 3. Sample cumulative fraction value (uniform distribution [0 1]) 4. Find inverse value Sample Hot water Sampled efficiency CF value (%) 1 0. 81 0. 91 2 0. 27 0. 62 3 0. 63 0. 89

Stochastic Simulation Steps • Step 1: Define the model • Step 2: Identify the uncertain parameters and dependencies • Step 3: Specify a probability distribution for each uncertain parameter • Step 4: Sample values for each uncertain parameter and propagate uncertainties and dependencies (simulate) • Step 5: Repeat Step #4 a large number of times!

2. Apply Monte Carlo Methods in Water Resources Optimization Problems

Example 1. How do uncertain initial reservoir storage and inflows affect total net benefits (HW #7)? Table 1. Flow likelihood in Month 1 Assume: Use 250 samples Prob. (%) CF (%) 1 0. 1 3 0. 4 5 0. 4 0. 8 8 0. 2 1. 0 Table 2. Transition probabilities Flow in Time t+1 Flow in Time t • Initial storage varies uniformly between 0. 5 and 10 units • Inflow in month 1 varies according to observations (Table 1) • Inflows in subsequent months exhibit lag-1 correlation (Table 2) • Flow at A must be at least 1 unit or 20% of largest simulated flow Flow 1 3 5 8 1 0. 2 0. 5 0. 2 0. 1 3 0. 2 0. 3 0. 2 5 0. 1 0. 4 0. 1 8 0. 2 0. 3 0. 4 0. 1

Example 2. Modeling Water Use by Households in Jordan • Insufficient/unreliable public supplies • Complex (tiered) rate structures • Municipal water often considered unsafe to drink • Expensive alternative sources • Limited water conservation data IRAN PAL. EGYPT SAUDI ARABIA Red Sea • Significant differences among users Right: Tanker truck refills storage tank Far Right: Rooftop water tanks 12

Modeling Approach 1. Identify options 2. Characterize options 3. Describe interdependencies Top: Treatment barrels for grey-water reuse (CSBE) 4. Identify availability events 5. 6. Above: Low-flow faucet, bidet, and toilet Optimize Repeat for a wide range of data values Right: Drinking water shop sells 20 -liter jugs 13

What decision variables are needed to model household options? 14

Non-linear program with recourse • Objective: Minimize expected annual costs [Eq 1] • 1 st stage actions: Infrastructure investments (Lhi) • Stochastic events: Public water availability (e) • 2 nd stage actions: Public and alternative supply uses; behavior modifications (Shje) • Subject to: – Meet water requirements in each event Upper limits on actions – Mass balance – Storage capacity – Block pricing on network use 1 st Event 2 nd Stage = Decision = State where stochastic information acquired 15

Characterize action costs and effectiveness Above: Drip irrigation store 16

Run optimization many times (with different parameter values) to represent residential users in Amman, Jordan

Calibrate to the distribution of piped water use • 500 Monte. Carlo simulated households • Adjust occupancy parameter (vacant residences) 18

Distributions of water savings for conservation actions in Amman (error bars represent 10 th and 90 th percentiles) 19

Major Findings 1. Modeling integrates source, availability, quality, storage, costs, conservation, and user behaviors. 2. Empirically estimate water use in Amman, Jordan. 3. Simultaneous output of: § Conservation technology adoption § Water use response § Household willingness-to-pay 4. Target conservation to select customers. Above: Store selling rooftop water tanks . Rosenberg et al, (2007) “Modeling Integrated Water-User Decisions in Intermittent Supply Systems. " Water Resources Research. 43. W 07425. 20

Monte Carlo Wrap Up • Powerful tool to incorporate real world uncertainties • Also provides probabilistic outputs • Offers water system management and policy insights not available from deterministic analysis