Monte Carlo method generate M random permutations of







![Lower bounds for sorting by comparisons yes/no questions: is A[i]>A[j] ? data are not Lower bounds for sorting by comparisons yes/no questions: is A[i]>A[j] ? data are not](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-9.jpg)
![Lower bounds for sorting by comparisons yes/no questions: is A[i]>A[j] ? A[1. . n] Lower bounds for sorting by comparisons yes/no questions: is A[i]>A[j] ? A[1. . n]](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-10.jpg)

![Lower bounds for search in sorted array INPUT: array A[1. . n], element x Lower bounds for search in sorted array INPUT: array A[1. . n], element x](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-12.jpg)
![Lower bounds for search in sorted array INPUT: array A[1. . n], element x Lower bounds for search in sorted array INPUT: array A[1. . n], element x](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-13.jpg)
![Lower bounds for minimum INPUT: array A[1. . n] OUTPUT: the smallest element of Lower bounds for minimum INPUT: array A[1. . n] OUTPUT: the smallest element of](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-14.jpg)
![Lower bounds for minimum INPUT: array A[1. . n] OUTPUT: the smallest element of Lower bounds for minimum INPUT: array A[1. . n] OUTPUT: the smallest element of](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-15.jpg)
![Counting sort array A[1. . n] containing numbers from {1, …, k} 1 st Counting sort array A[1. . n] containing numbers from {1, …, k} 1 st](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-16.jpg)
![Counting sort array A[1. . n] containing numbers from {1, …, k} for i Counting sort array A[1. . n] containing numbers from {1, …, k} for i](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-17.jpg)
![for i 1 to k do C[i] 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-18.jpg)
![for i 1 to k do C[i] 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-19.jpg)
![for i 1 to k do C[i] 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-20.jpg)
![for i 1 to k do C[i] 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-21.jpg)
![for i 1 to k do C[i] 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-22.jpg)
![Counting sort for i 1 to k do C[i] 0 for j 1 to Counting sort for i 1 to k do C[i] 0 for j 1 to](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-23.jpg)
![Counting sort for i 1 to k do C[i] 0 for j 1 to Counting sort for i 1 to k do C[i] 0 for j 1 to](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-24.jpg)
![Counting sort for i 1 to k do C[i] 0 for j 1 to Counting sort for i 1 to k do C[i] 0 for j 1 to](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-25.jpg)
![Radix sort array A[1. . n] containing numbers from {0, …, k 2 - Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-26.jpg)
![Radix sort array A[1. . n] containing numbers from {0, …, k 2 - Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-27.jpg)
![Radix sort array A[1. . n] containing numbers from {0, …, k 2 - Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-28.jpg)
![Radix sort array A[1. . n] containing numbers from {0, …, k 2 - Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-29.jpg)
![Radix sort array A[1. . n] containing numbers from {0, …, k 2 - Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-30.jpg)
![Radix sort array A[1. . n] containing numbers from {0, …, kd - 1} Radix sort array A[1. . n] containing numbers from {0, …, kd - 1}](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-31.jpg)
![Radix sort array A[1. . n] containing numbers from {0, …, kd - 1} Radix sort array A[1. . n] containing numbers from {0, …, kd - 1}](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-32.jpg)
![Radix sort array A[1. . n] containing numbers from {0, …, kd - 1} Radix sort array A[1. . n] containing numbers from {0, …, kd - 1}](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-33.jpg)





![Bucket sort for i 1 to n do insert A[i] into list B[ A[i]*n Bucket sort for i 1 to n do insert A[i] into list B[ A[i]*n](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-39.jpg)
![Bucket sort for i 1 to n do insert A[i] into list B[ A[i]*n Bucket sort for i 1 to n do insert A[i] into list B[ A[i]*n](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-40.jpg)
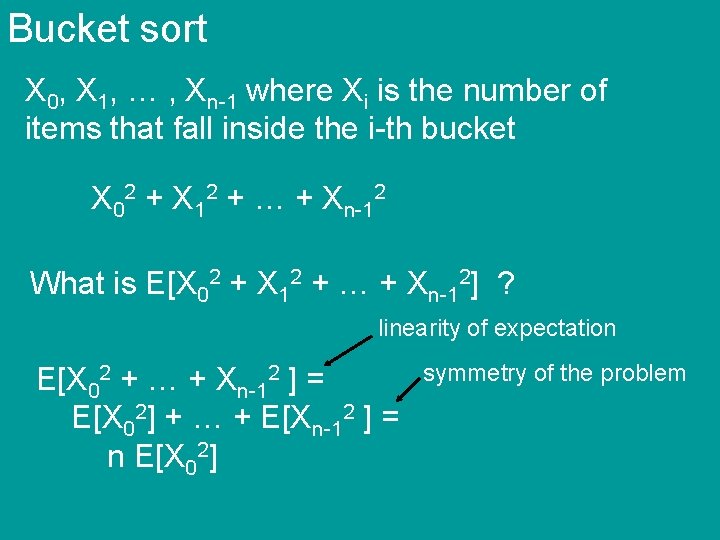
![Bucket sort E[X 02] What is E[X 0] ? p=1/n value of X 0 Bucket sort E[X 02] What is E[X 0] ? p=1/n value of X 0](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-42.jpg)
![Bucket sort E[X 02] p=1/n E[X 0] = 1 0 1 (1 -p)n n Bucket sort E[X 02] p=1/n E[X 0] = 1 0 1 (1 -p)n n](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-43.jpg)
![Bucket sort p=1/n E[X 02] E[X 0] = 1 n E[X 0] = k Bucket sort p=1/n E[X 02] E[X 0] = 1 n E[X 0] = k](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-44.jpg)
![Bucket sort p=1/n E[X 02] E[X 0] = 1 n E[X 0] = n* Bucket sort p=1/n E[X 02] E[X 0] = 1 n E[X 0] = n*](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-45.jpg)
![Bucket sort E[X 02] 0 1 (1 -p)n n (1 -p) n-1 k binomial(n, Bucket sort E[X 02] 0 1 (1 -p)n n (1 -p) n-1 k binomial(n,](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-46.jpg)
![Bucket sort p=1/n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0 Bucket sort p=1/n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-47.jpg)
![Bucket sort p=1/n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0 Bucket sort p=1/n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-48.jpg)
![Bucket sort p=1/n E[X 02]= k(k-1) * binomial(n, k) pk (1 -p)n-k k=2 +n*p Bucket sort p=1/n E[X 02]= k(k-1) * binomial(n, k) pk (1 -p)n-k k=2 +n*p](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-49.jpg)
- Slides: 49

“Monte Carlo method” generate M random permutations of {1, …, 20} let H be the number of those in which exactly one person gets his/her card back output H/M

Lower bounds number from {1, 2, 3, …, 9} 3 yes/no questions Can you always figure out the number?

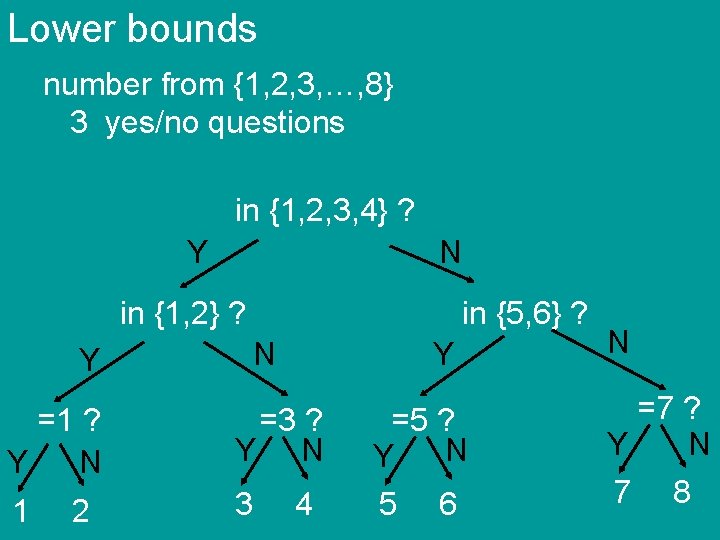
Lower bounds number from {1, 2, 3, …, 8} 3 yes/no questions Can you always figure out the number?

Lower bounds number from {1, 2, 3, …, 8} 3 yes/no questions in {1, 2, 3, 4} ? Y N in {1, 2} ? in {5, 6} ? N Y Y =1 ? Y N =3 ? Y N 1 3 2 4 =5 ? N Y 5 6 N =7 ? Y N 7 8

Lower bounds number from {1, 2, 3, …, n} k yes/no questions

Lower bounds number from {1, 2, 3, …, n} k yes/no questions k = log 2 n

Lower bounds number from {1, 2, 3, …, n} k yes/no questions k = log 2 n INFORMATION THEORETIC LOWER BOUND: k log 2 n

Lower bounds n animals = {dog, cat, fish, eagle, snake, …} yes/no questions INFORMATION THEORETIC LOWER BOUND: k log 2 n
![Lower bounds for sorting by comparisons yesno questions is AiAj data are not Lower bounds for sorting by comparisons yes/no questions: is A[i]>A[j] ? data are not](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-9.jpg)
Lower bounds for sorting by comparisons yes/no questions: is A[i]>A[j] ? data are not used to “control” computation in any other way A[1. . n] 1 2 1 3 2 1 1. 3 3 1 3 2 3 1 2 1
![Lower bounds for sorting by comparisons yesno questions is AiAj A1 n Lower bounds for sorting by comparisons yes/no questions: is A[i]>A[j] ? A[1. . n]](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-10.jpg)
Lower bounds for sorting by comparisons yes/no questions: is A[i]>A[j] ? A[1. . n] log a*b = log a + log b k log 2 n! log 2 n + log 2 (n-1) + … log 2 1 (n/2) log 2 (n/2) = (n log n)

Lower bounds for sorting Theorem: Any comparison based sorting algorithm requires (n ln n) comparisons in the worst-case.
![Lower bounds for search in sorted array INPUT array A1 n element x Lower bounds for search in sorted array INPUT: array A[1. . n], element x](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-12.jpg)
Lower bounds for search in sorted array INPUT: array A[1. . n], element x OUTPUT: a position of x in A if x is in A otherwise
![Lower bounds for search in sorted array INPUT array A1 n element x Lower bounds for search in sorted array INPUT: array A[1. . n], element x](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-13.jpg)
Lower bounds for search in sorted array INPUT: array A[1. . n], element x OUTPUT: a position of x in A if x is in A otherwise Theorem: Any comparison based algorithm for searching an element in a sorted array requires (ln n) comparisons in the worst-case.
![Lower bounds for minimum INPUT array A1 n OUTPUT the smallest element of Lower bounds for minimum INPUT: array A[1. . n] OUTPUT: the smallest element of](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-14.jpg)
Lower bounds for minimum INPUT: array A[1. . n] OUTPUT: the smallest element of A
![Lower bounds for minimum INPUT array A1 n OUTPUT the smallest element of Lower bounds for minimum INPUT: array A[1. . n] OUTPUT: the smallest element of](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-15.jpg)
Lower bounds for minimum INPUT: array A[1. . n] OUTPUT: the smallest element of A INFORMATION THEORETIC LOWER BOUND: at least (ln n) comparisons ADVERSARY LOWER BOUND: at least (n) comparisons
![Counting sort array A1 n containing numbers from 1 k 1 st Counting sort array A[1. . n] containing numbers from {1, …, k} 1 st](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-16.jpg)
Counting sort array A[1. . n] containing numbers from {1, …, k} 1 st pass: count how many times i {1, …, k} occurs 2 nd pass: put the elements in B
![Counting sort array A1 n containing numbers from 1 k for i Counting sort array A[1. . n] containing numbers from {1, …, k} for i](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-17.jpg)
Counting sort array A[1. . n] containing numbers from {1, …, k} for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=0 for I 1 to k+1 do D[i+1] D[i]+C[i] for j 1 to n do D[A[j]]++ B[ D[A[j]] ] A[j]
![for i 1 to k do Ci 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-18.jpg)
for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=1 for I 1 to k-1 do D[i+1] D[i]+C[i] Counting sort for j 1 to n do B[ D[A[j]] ] A[j] D[A[j]]++ 1232242112332124 C D 4 1 7 5 3 12 2 15
![for i 1 to k do Ci 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-19.jpg)
for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=1 for I 1 to k-1 do D[i+1] D[i]+C[i] Counting sort for j 1 to n do B[ D[A[j]] ] A[j] D[A[j]]++ 1232242112332124 C D 4 2 1 7 5 3 12 2 15
![for i 1 to k do Ci 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-20.jpg)
for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=1 for I 1 to k-1 do D[i+1] D[i]+C[i] Counting sort for j 1 to n do B[ D[A[j]] ] A[j] D[A[j]]++ 1232242112332124 C D 4 2 1 7 6 3 12 2 2 15
![for i 1 to k do Ci 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-21.jpg)
for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=1 for I 1 to k-1 do D[i+1] D[i]+C[i] Counting sort for j 1 to n do B[ D[A[j]] ] A[j] D[A[j]]++ 1232242112332124 C D 4 2 1 7 6 3 13 2 2 15 3
![for i 1 to k do Ci 0 for j 1 to n do for i 1 to k do C[i] 0 for j 1 to n do](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-22.jpg)
for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=1 for I 1 to k-1 do D[i+1] D[i]+C[i] Counting sort for j 1 to n do B[ D[A[j]] ] A[j] D[A[j]]++ 1232242112332124 C D 4 2 1 7 7 3 13 2 2 2 15 3
![Counting sort for i 1 to k do Ci 0 for j 1 to Counting sort for i 1 to k do C[i] 0 for j 1 to](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-23.jpg)
Counting sort for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=1 for I 1 to k-1 do D[i+1] D[i]+C[i] for j 1 to n do B[ D[A[j]] ] A[j] D[A[j]]++ 1232242112332124 C D 4 5 7 12 3 15 2 17 1 1 2 2 2 2 3 3 3 4 4
![Counting sort for i 1 to k do Ci 0 for j 1 to Counting sort for i 1 to k do C[i] 0 for j 1 to](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-24.jpg)
Counting sort for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=1 for I 1 to k-1 do D[i+1] D[i]+C[i] for j 1 to n do B[ D[A[j]] ] A[j] D[A[j]]++ stable sort = after sorting the items with the same key don’t switch order running time = O(n+k)
![Counting sort for i 1 to k do Ci 0 for j 1 to Counting sort for i 1 to k do C[i] 0 for j 1 to](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-25.jpg)
Counting sort for i 1 to k do C[i] 0 for j 1 to n do C[A[j]]++ D[1]=1 for I 1 to k-1 do D[i+1] D[i]+C[i] for j 1 to n do B[ D[A[j]] ] A[j] D[A[j]]++ stable sort = after sorting the items with the same key don’t switch order running time = O(n+k) What if e. g. , k = n 2 ?
![Radix sort array A1 n containing numbers from 0 k 2 Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-26.jpg)
Radix sort array A[1. . n] containing numbers from {0, …, k 2 - 1} 1) sort using counting sort with key = x mod k 2) sort using counting sort with key = x/k Running time = ?
![Radix sort array A1 n containing numbers from 0 k 2 Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-27.jpg)
Radix sort array A[1. . n] containing numbers from {0, …, k 2 - 1} 1) sort using counting sort with key = x mod k 2) sort using counting sort with key = x/k Running time = O(n + k)
![Radix sort array A1 n containing numbers from 0 k 2 Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-28.jpg)
Radix sort array A[1. . n] containing numbers from {0, …, k 2 - 1} example k=10 28 21 42 43 23 32 70 18 29 20 70 20 21 42 32 43 23 28 18 29
![Radix sort array A1 n containing numbers from 0 k 2 Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-29.jpg)
Radix sort array A[1. . n] containing numbers from {0, …, k 2 - 1} example k=10 28 21 42 43 23 32 70 18 29 20 70 20 21 42 32 43 23 28 18 29
![Radix sort array A1 n containing numbers from 0 k 2 Radix sort array A[1. . n] containing numbers from {0, …, k 2 -](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-30.jpg)
Radix sort array A[1. . n] containing numbers from {0, …, k 2 - 1} example k=10 28 21 42 43 23 32 70 18 29 20 70 20 21 42 32 43 23 28 18 29 18 20 21 23 28 29 32 42 43 70
![Radix sort array A1 n containing numbers from 0 kd 1 Radix sort array A[1. . n] containing numbers from {0, …, kd - 1}](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-31.jpg)
Radix sort array A[1. . n] containing numbers from {0, …, kd - 1} 1) sort using counting sort with key = x mod k 2) sort using counting sort with key = x/k mod k 3) sort using counting sort with key = x/k 2 mod k … d) sort using counting sort with key = x/kd-1 mod k
![Radix sort array A1 n containing numbers from 0 kd 1 Radix sort array A[1. . n] containing numbers from {0, …, kd - 1}](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-32.jpg)
Radix sort array A[1. . n] containing numbers from {0, …, kd - 1} Correctness: after s-th step the numbers are sorted according to x mod ks Proof: By induction. Base case s=1 is trivial. 1) sort using counting sort with key = x mod k
![Radix sort array A1 n containing numbers from 0 kd 1 Radix sort array A[1. . n] containing numbers from {0, …, kd - 1}](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-33.jpg)
Radix sort array A[1. . n] containing numbers from {0, …, kd - 1} Correctness: after s-th step the numbers are sorted according to x mod ks Proof: Now assume IH and execute s+1 st step. Let x, y be such that x mod ks+1 < y mod ks+1. Then either x/ks mod k < y/ks mod k or x/ks mod k = y/ks mod k and x mod ks < y mod ks

Bucket sort linear time sorting algorithm on average Assume some distribution on input. INPUT: n independently random numbers from the uniform distribution on the interval [0, 1].

Bucket sort INPUT: n independently random numbers from the uniform distribution on the interval [0, 1]. for i 1 to n do insert A[i] into list B[ A[i]*n ] for i 0 to n-1 do sort list B[i] output lists B[0], …, B[n-1]

Bucket sort INPUT: n independently random numbers from the uniform distribution on the interval [0, 1]. 0. 13, 0. 23, 0. 56, 0. 74, 0. 18, 0. 34, 0. 12, 0. 82, 0. 14, 0. 19 for i 1 to n do insert A[i] into list B[ A[i]*n ] for i 0 to n-1 do sort list B[i] output lists B[0], …, B[n-1]

Bucket sort INPUT: n independently random numbers from the uniform distribution on the interval [0, 1]. 0. 13, 0. 23, 0. 56, 0. 74, 0. 18, 0. 34, 0. 12, 0. 52, 0. 14, 0. 19 1 2 5 7 1 3 1 5 1 B[1]: 0. 13, 0. 18, 0. 12, 0. 14, 0. 19 B[2]: 0. 23 for i 1 to n do B[3]: 0. 34 insert A[i] into list B[ B[5]: 0. 56, 0. 52 B[7]: 0. 74 for i 0 to n-1 do 1 A[i]*n ] sort list B[i] output lists B[0], …, B[n-1]

Bucket sort INPUT: n independently random numbers from the uniform distribution on the interval [0, 1]. 0. 13, 0. 23, 0. 56, 0. 74, 0. 18, 0. 34, 0. 12, 0. 52, 0. 14, 0. 19 1 2 5 7 1 3 1 5 1 B[1]: 0. 12, 0. 13, 0. 14, 0. 18, 0. 19 B[2]: 0. 23 for i 1 to n do B[3]: 0. 34 insert A[i] into list B[ B[5]: 0. 52, 0. 56 B[7]: 0. 74 for i 0 to n-1 do 1 A[i]*n ] sort list B[i] output lists B[0], …, B[n-1]
![Bucket sort for i 1 to n do insert Ai into list B Ain Bucket sort for i 1 to n do insert A[i] into list B[ A[i]*n](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-39.jpg)
Bucket sort for i 1 to n do insert A[i] into list B[ A[i]*n ] for i 0 to n-1 do sort list B[i] output lists B[0], …, B[n-1] assume we use insert-sort worst-case running time?
![Bucket sort for i 1 to n do insert Ai into list B Ain Bucket sort for i 1 to n do insert A[i] into list B[ A[i]*n](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-40.jpg)
Bucket sort for i 1 to n do insert A[i] into list B[ A[i]*n ] for i 0 to n-1 do sort list B[i] output lists B[0], …, B[n-1] assume we use insert-sort average-case running time? X 0, X 1, … , Xn-1 where Xi is the number of items that fall inside the i-th bucket
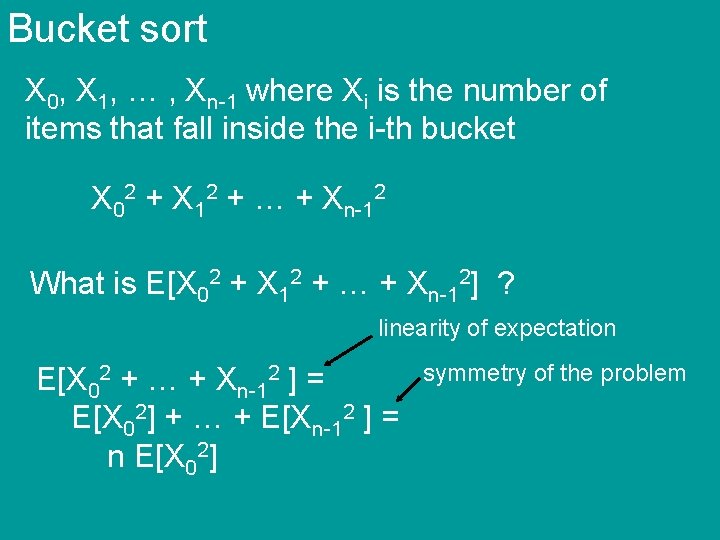
Bucket sort X 0, X 1, … , Xn-1 where Xi is the number of items that fall inside the i-th bucket X 02 + X 12 + … + Xn-12 What is E[X 02 + X 12 + … + Xn-12] ? linearity of expectation E[X 02 + … + Xn-12 ] = E[X 02] + … + E[Xn-12 ] = n E[X 02] symmetry of the problem
![Bucket sort EX 02 What is EX 0 p1n value of X 0 Bucket sort E[X 02] What is E[X 0] ? p=1/n value of X 0](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-42.jpg)
Bucket sort E[X 02] What is E[X 0] ? p=1/n value of X 0 0 1 (1 -p)n n (1 -p) n-1 k binomial(n, k) pk (1 -p)n-k n pn
![Bucket sort EX 02 p1n EX 0 1 0 1 1 pn n Bucket sort E[X 02] p=1/n E[X 0] = 1 0 1 (1 -p)n n](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-43.jpg)
Bucket sort E[X 02] p=1/n E[X 0] = 1 0 1 (1 -p)n n (1 -p) n-1 k binomial(n, k) pk (1 -p)n-k n pn n E[X 0] = k * binomial(n, k) p k=0 k (1 -p)n-k
![Bucket sort p1n EX 02 EX 0 1 n EX 0 k Bucket sort p=1/n E[X 02] E[X 0] = 1 n E[X 0] = k](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-44.jpg)
Bucket sort p=1/n E[X 02] E[X 0] = 1 n E[X 0] = k * binomial(n, k) p k (1 -p)n-k k=1 binomial (n, k) = (n/k) * binomial (n-1, k-1) n binomial(n, k) p k=0 k (1 -p)n-k = 1
![Bucket sort p1n EX 02 EX 0 1 n EX 0 n Bucket sort p=1/n E[X 02] E[X 0] = 1 n E[X 0] = n*](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-45.jpg)
Bucket sort p=1/n E[X 02] E[X 0] = 1 n E[X 0] = n* binomial(n-1, k-1) p k=1 = n*p (1 -p)n-k n binomial(n-1, k-1) p k=1 = n*p n binomial(n, k) p k=0 k k (1 -p)n-k = 1 k-1(1 -p)n-k
![Bucket sort EX 02 0 1 1 pn n 1 p n1 k binomialn Bucket sort E[X 02] 0 1 (1 -p)n n (1 -p) n-1 k binomial(n,](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-46.jpg)
Bucket sort E[X 02] 0 1 (1 -p)n n (1 -p) n-1 k binomial(n, k) pk (1 -p)n-k n pn n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0 p=1/n
![Bucket sort p1n EX 02 k 2 binomialn k pk 1 pnk k0 Bucket sort p=1/n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-47.jpg)
Bucket sort p=1/n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0 n = k * binomial(n, k) pk (1 -p)n-k k=0 n k=0 + k(k-1) * binomial(n, k) pk (1 -p)n-k
![Bucket sort p1n EX 02 k 2 binomialn k pk 1 pnk k0 Bucket sort p=1/n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-48.jpg)
Bucket sort p=1/n E[X 02]= k 2 * binomial(n, k) pk (1 -p)n-k k=0 n n*p = k * binomial(n, k) pk (1 -p)n-k k=0 n k=0 + k(k-1) * binomial(n, k) pk (1 -p)n-k
![Bucket sort p1n EX 02 kk1 binomialn k pk 1 pnk k2 np Bucket sort p=1/n E[X 02]= k(k-1) * binomial(n, k) pk (1 -p)n-k k=2 +n*p](https://slidetodoc.com/presentation_image_h2/ade0d8fd3e9fbf2c0fba7ccdb95eb878/image-49.jpg)
Bucket sort p=1/n E[X 02]= k(k-1) * binomial(n, k) pk (1 -p)n-k k=2 +n*p binomial (n, k) = (n/k) * binomial (n-1, k-1) = (n/k) * ((n-1)/(k-1)) * binomial (n-2, k-2) E[X 02] = n* (n-1) * p 2 + n*p