Monopole Transitions in Light Unstable Nuclei Makoto Ito

Monopole Transitions in Light Unstable Nuclei Makoto Ito 1, 2 1 Department 2 Rsearch of Pure and Applied Physics, Kansai University Center of Nuclear Physics (RCNP), Osaka University Contents I. Introduction II. Previous analysis on 10 Be and 12 Be III. Features of Isoscalar monopole transition IV. Isoscalar monopole transition in 12 Be V. Analysis of the miirror system of 10 Be with 10 C VI. Summary and future studies

IKEDA Diagram Cluster structures in 4 N nuclei Ikeda’s Threshold rules Molecular structures will appear close to the respective cluster threshold. Be isotopes Molecular Orbital (MO) picture α-Particle ⇒ Stable p― s+ 3 H+p ～ 20 Me. V Systematic Appearance of a cluster structures The MO model gives one of standard picture in the low-lying structure

Extension of the MO model Structure changes beyond MO will occur in the highly excited states Extension of the MO model is important Generalized Two-center Cluster Model (Example of 10 Be) Dimer channels 10 Be=a+a+N+N Mol. Orb. a Combine 6 He 5 He Unified model between M. O. and Dimer channels : ROP 77 (2015) Y= C 1 + C 2 + 0 Pi (i=x, y, z) Coupled channels with Atomic orbitals 5 He . . . S C 3 S, Ci : Variational PRM.

Unified studies of structures and reactions: 10 Be and 12 Be (Jp=0+) Structures becomes abundant by adding two extra neutrons α + 2 N α+6 He Exp: D. Suzuki α + 4 N α+8 He Exp: M. Freer Essential picture of structure is a hybrid of the α-cluster + excess neutrons

Monopole excitation and cluster structures Enhancement of the monopole transition is a sign of the development of the cluster structure in final states Cluster structure Monopole and Clusters 2 hw excitation of the clusters’ rel. motion Shell model = Melted Cluster = Developed cluster 2 hw ex. Monopole operator induces 2 hw Ex. for the clusters in G. S. Bayman-Bohr Theorem Strength in Ex<10 Me. V is possible T. Yamada et al. , PTP 120 (08) ( Lower strength is difficult in shell model )

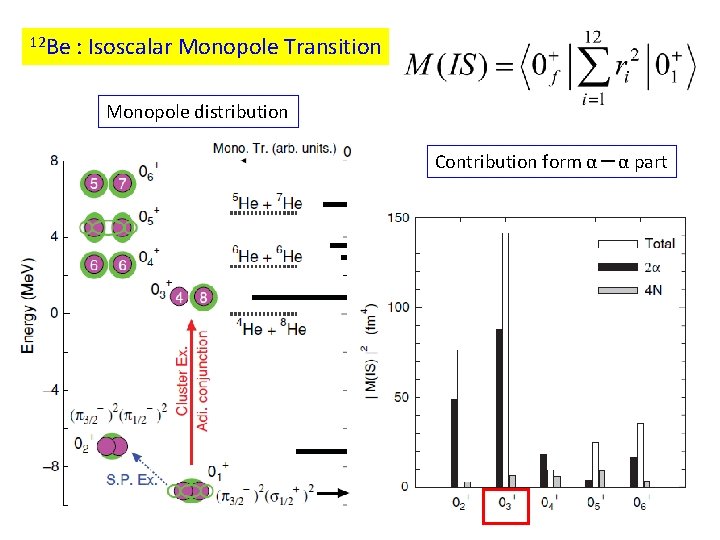
12 Be : Isoscalar Monopole Transition Monopole distribution Contribution form α－α part

He-He Relative wave function for the 01+ and 03+ states The 01+ state (Deformed MO) The 03+ state (Developed α + 8 Heg. s. ) α + 8 Heg. s. r γ(r) ( fm-1/2 ) 2 hw Ex. 6 He g. s. r ( fm ) + 6 Heg. s. 6 He g. s. + 6 Heg. s. r ( fm ) Radial excitation of the relative wave function occurs in 01+ ⇒ 03+

Monopole strength of 12 Be： Ratio to S. P. strength Simple shell model is difficult to explain M(IS) strength below E～ 20 Me. V ! T. Yamada et al. , PTP. 120, 1139 (2008) Ex. Energy (Me. V) 2. 12 10. 19 12. 29 Recently measured by Chinese Group 12. 94 15. 09 All the excited states have a comparable to or a few times larger strength in comparison to the S. P. strength.

Recent measurement of isoscalar monopole strength in 12 Be 12 C + 12 Be ⇒ 12 C + (4 He+8 He) Z. H. Yang et al. , PRL 112 (2014) Ex = 10. 3 Me. V dσ/d. Ex 4 He + 8 He band head at Ex = 10. 3 Me. V M(IS)exp. = 7. 0 ± 1. 0 fm 2 M(IS; 01+⇒ 03+)theory = 11. 9 fm 2 Decay effect of the 10. 3 Me. V resonance into 4 He+8 He should be included in theory

Variety of Nuclear Chemical Clusters 12 Be Question = α + 4 N Structure is abundant What is a variation in replacing α core or valence neutrons ? ROP 77 096301 (2014) + 2 N 2 N ⇒ 2 P α ⇒ 12 C 10 Be = α + 2 N Coulomb Shift (Thomas-Ehrman) 10 C = α + 2 P 18 O = α + 12 C + 2 N

10 Be 0 4+ Energy ( Me. V ) 0 3+ α Th. 02 + Jp=0+ Levels 10 C (p-)2 1. 6 Me. V 2+ 0. 9 Me. V Developed Cluster (S-wave) (s+)2 1. 3 Me. V Suppressed Coulomb shift (p-)2 01 + In continuum, we solved the scattering problem 2. 3 Me. V

10 Be Jp=0+ Levels (2) 10 C 0 4+ ⇒ consistent to PRC 86 (14) + ( Traditional TES is < 0. 4 Me. V ) Reduced Ex. energy will enhance the 01+ ⇒ 02+ monopole transition α Th. 02 α Th. + 0 1+ Reduced Excitation Energy ( Me. V ) 03 Cluster TES of 02+ is ～ 1 Me. V Cluster’s Thomas Ehrman Shift (Cluster TES)

Monopole transition in 10 C and 0 1+ 10 Be 0 3+ 4 2 hw Cluster ex. Theoretical Prediction of M(IS) r. m. s. ( fm ) E(02+) ( Me. V ) 6 M(IS) ( fm 2 ) Theory 01 + ⇒ 02 + 01 + ⇒ 03 + 01 + ⇒ 04 + 10 Be 2. 66 4. 90 2. 78 8. 26 4. 00 10 C 2. 73 4. 00 5. 27 7. 55 2. 90 MO EX. Cluster EX. MO EX. 1. All the strengths are comparable to or larger than M(IS)S. P. = 3. 37 fm 2 ⇒ M(IS) is prominently enhanced for the clusters’ relative excitation. 2. M(IS) of 01+ ⇒ 02+ is not charge-symmetric in 10 Be and 10 C ⇒ Due to the Cluster TES appearing n 10 C.

Summary Review Article: M. Ito and K. Ikeda, Rep. on Prog. in Phys. , 77 096301 (2014) We have investigated the structure changes of the two-center systems over the wide energy region. The importance of the monopole transition is also discussed. Results 1. Structure analysis of the light two-centers nuclei, 10, 12 Be ① Various chemical-bonding-like structures appears in excited states ② Wide variety appears by the combination of cluster-core and excess-nucleons 2. Analysis of the mirror system, 10 Be and 10 C ① Suppression of the Coulomb shift ⇒ Suppression occur in the cluster state (Large mixture of S-wave component) ② Monopole transition ⇒ Asymmetry in the 01+ ⇒ 02+ transition is predicted Structure changes and the monopole transitions should be investigated over a wide energy region, covering the scattering continuum states.

Thomas Ehrman shift Bohr-Mottelson Nuclear Structre Vol. 1 E E [Me. V] 3/2+ Coulomb repulsion is suppressedd 3/2 for the S-wave orbit configuration ⇒ Peculiarity of S-wave 16 O 4 3 0 3/2+ 16 O +N 5/2+ Coulomb Shift -1 -2 -3 1/2+ -4 5/2+ -5 4 3 2 2 1 [Me. V] 17 O Exp. 17 F Exp. d 3/2 s 1/2 d 5/2 Energy shift of S-wave states Seems to be prominent ⇒ Thomas Ehrman shift (TES) 　　⊿E　= 370 ke. V 1 0 -1 -2 s 1/2 -3 d 5/2 -4 17 O Calc. 17 F Calc. -5

Large Energy for a neutron excitation ⇒ Degeneracy of two levels Comparison of 10 Be with 18 O (Theory) 10 Be = (α+6 He) +(5 He+5 He) 18 O = (α+14 C) +(5 He+13 C) 03 + α+6 He(21+) α+14 C Covalent state Energy ( Me. V ) 03 + (s+)2 Cluster Ex. ～ 10 Me. V 02 + Neutron Ex. Neutron EX. ～ 5 Me. V Cluster Ex. ～ 8 Me. V Shell model (p-)2 01 + Coupling effect of neutron ex. and Cluster ex. is small. 01 + Coupling effect of neutron ex. and Cluster ex. is Large.

Shift of the excitation energies 0 2+ 0 4+ 0 5+ Cluster Shell Ex. (10 Be) Me. V 4. 9 11. 6 13. 8 Ex. (10 C ) Me. V 4. 0 10. 2 14. 5 ⊿Ex(Th. ) 0. 9 1. 4 0. 7 ⊿Ex(Exp. ) 0. 9※ ? ? ※ Compilation shown in PRC 86, 044314 (2014) Theoretical calculation predict the Cluster TES of ⊿E > 0. 9 Me. V ⇒ Much larger than the old Thomas Ehrman shift (⊿E < 0. 4 Me. V)

Example of the 16 O nucleus T. Yamada et al. , Phys. Rev. C 85, 034315 (2012) = 4α OCM calculation RPA calculation 02 + 03 + 04, 5+ 06 + Discrete strength at Ex<15 Me. V is nicely reproduced Continuous strength at Ex>15 Me. V is reproduced. Discrete Lower strength (Cluster) + Continuous Higher strength (Mean field)

Shift of the excitation energies 0 2+ 0 3+ 0 4+ Cluster Shell Ex. (10 Be) Me. V 4. 9 11. 6 13. 8 Ex. (10 C ) Me. V 4. 0 10. 2 14. 5 ⊿Ex(Th. ) 0. 9 1. 4 0. 7 ⊿Ex(Exp. ) 0. 9※ ? ? ※ Compilation shown in PRC 86, 044314 (2014) Theoretical calculation predict the Cluster TES of ⊿E > 0. 9 Me. V ⇒ Much larger than the traditional Thomas-Ehrman shift in 17 O-17 F (⊿E < 0. 4 Me. V)