MomentumSpace Renormalization Group Transformation in Bayesian Image Modeling

Momentum-Space Renormalization Group Transformation in Bayesian Image Modeling by Gaussian Graphical Model Kazuyuki Tanaka GSIS, Tohoku University, Sendai, Japan http: //www. smapip. is. tohoku. ac. jp/~kazu/ Collaborators Masayuki Ohzeki (Tohoku University, Japan) Muneki Yasuda (Yamagata University, Japan) Shun Kataoka (Otaru University of Commerce, Japan) March, 2019 University of Roma, La Sapienza 1

Hyperparameter Estimation of Pairwise Markov Random Fields March, 2019 University of Roma, La Sapienza 2

Hyperparameter Estimation of Pairwise Markov Random Fields Prior Probability Pairwise MRF Data Generative Model 2 1 5 9 1 5 6 10 9 3 2 6 10 7 11 2 3 4 5 6 7 8 9 10 11 12 4 3 7 11 8 12 4 8 12 V: Set of all the nodes (vertices) March, 2019 1 University of Roma, La Sapienza E: Set of all the links (edges) 3

Hyperparameter Estimation of Pairwise Markov Random Fields Data Generative Model Prior Probability Pairwise MRF Joint Probability 9 V: Set of all the nodes (vertices) March, 2019 1 5 9 Unknown University of Roma, La Sapienza 2 3 4 5 6 7 8 9 10 11 12 2 1 Probability of Parameter a and Data d Likelihood of a and b 5 1 6 10 3 2 6 10 7 11 4 3 7 8 12 11 4 8 12 E: Set of all the links (edges) 4

Hyperparameter Estimation of Pairwise Markov Random Fields Data Generative Model Prior Probability Pairwise MRF Joint Probability 2 3 4 5 6 7 8 9 10 11 12 2 1 Probability of Data d Likelihood of a and b SS…S Marginal Likelihood V: Set of all the nodes (vertices) March, 2019 1 University of Roma, La Sapienza 1 2 12 5 9 1 5 9 6 10 3 2 6 10 7 11 4 3 7 8 12 11 4 8 12 E: Set of all the links (edges) 5

Hyperparameter Estimation of Pairwise Markov Random Fields Data Generative Model Prior Probability Pairwise MRF Joint Probability 1 2 3 4 5 6 7 8 9 10 11 12 2 1 Probability of Data d Likelihood of a and b SS…S Marginal Likelihood 1 2 12 5 9 1 5 9 6 10 3 2 6 10 7 11 4 3 7 8 12 11 Expectation Maximization (EM) Algorithm March, 2019 University of Roma, La Sapienza 8 12 Maximization of Marginal Likelihood V: Set of all the nodes (vertices) 4 E: Set of all the links (edges) 6

Bayesian Image Analysis by Gaussian Graphical Model Prior Probability V: Set of all the pixels E: Set of all the nearest-neighbour pairs of pixels March, 2019 Patterns are generated by MCMC. Markov Chain Monte Carlo Method University of Roma, La Sapienza 7

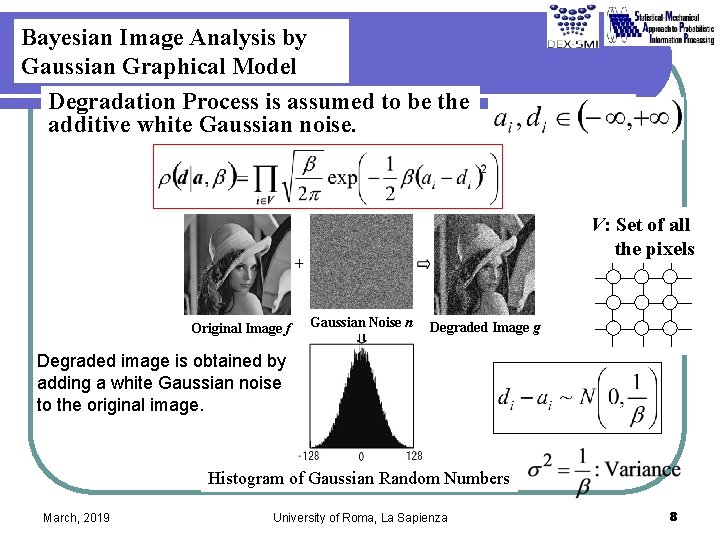
Bayesian Image Analysis by Gaussian Graphical Model Degradation Process is assumed to be the additive white Gaussian noise. V: Set of all the pixels Original Image f Gaussian Noise n Degraded Image g Degraded image is obtained by adding a white Gaussian noise to the original image. Histogram of Gaussian Random Numbers March, 2019 University of Roma, La Sapienza 8

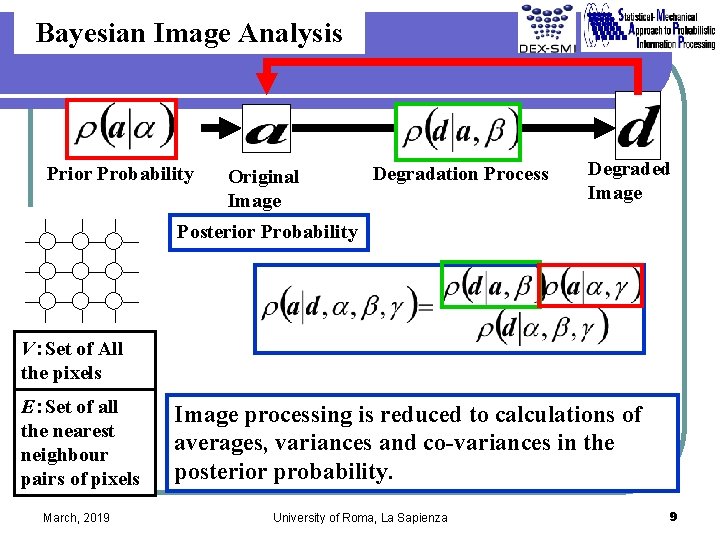
Bayesian Image Analysis Prior Probability Original Image Degradation Process Degraded Image Posterior Probability V：Set of All the pixels E：Set of all the nearest neighbour pairs of pixels March, 2019 Image processing is reduced to calculations of averages, variances and co-variances in the posterior probability. University of Roma, La Sapienza 9

Statistical Estimation of Hyperparameters a, b, g are determined so as to maximize the marginal likelihood Pr{Ｄ=d|a, b, g} with respect to a, b, g. Original Image Degraded Image Marginalized with respect to d Marginal Likelihood March, 2019 University of Roma, La Sapienza 10

Exact expression of Marginal Likelihood in Gaussian Graphical Model Multi-dimensional Gauss integral formula We can construct an exact EM algorithm. March, 2019 University of Roma, La Sapienza 11

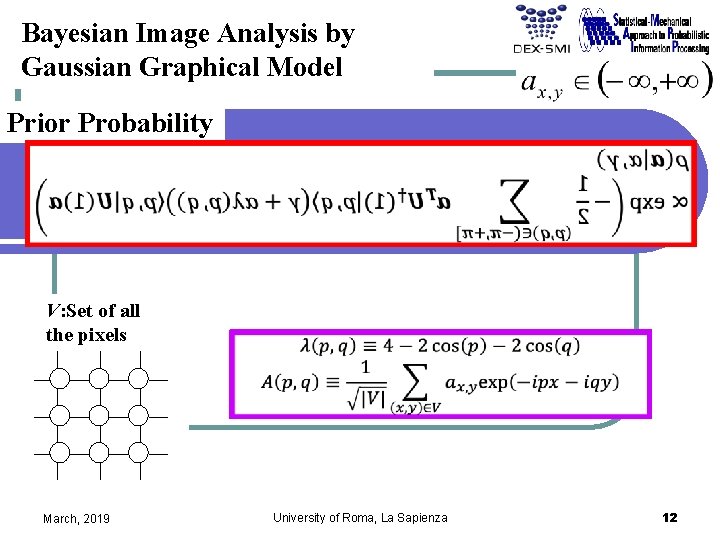
Bayesian Image Analysis by Gaussian Graphical Model Prior Probability V: Set of all the pixels March, 2019 University of Roma, La Sapienza 12

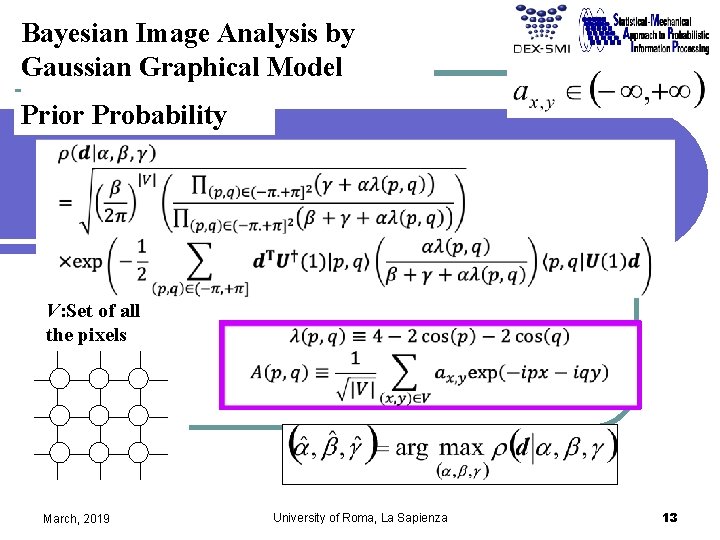
Bayesian Image Analysis by Gaussian Graphical Model Prior Probability V: Set of all the pixels March, 2019 University of Roma, La Sapienza 13

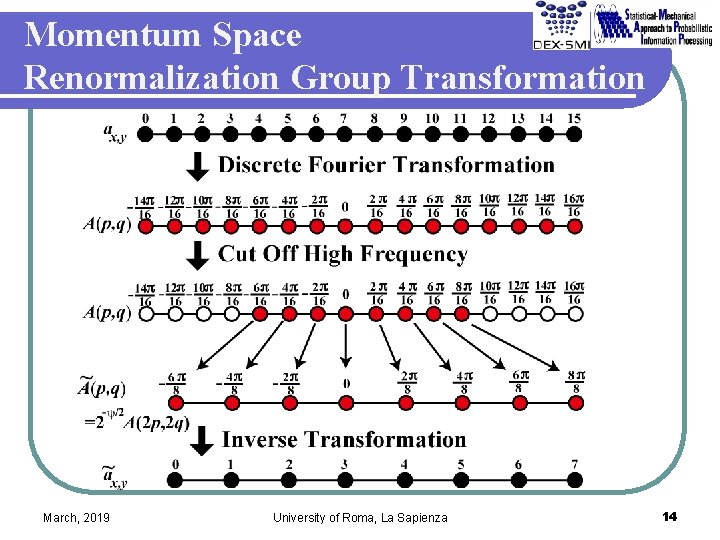
Momentum Space Renormalization Group Transformation March, 2019 University of Roma, La Sapienza 14

Momentum Space Renormalization Group Transformation March, 2019 University of Roma, La Sapienza 15

Momentum Space Renormalization Group Transformation March, 2019 University of Roma, La Sapienza 16

Momentum Space Renormalization Group Transformation inn Bayesian Noise Reduction by Gaussian Graphical Model March, 2019 University of Roma, La Sapienza 17

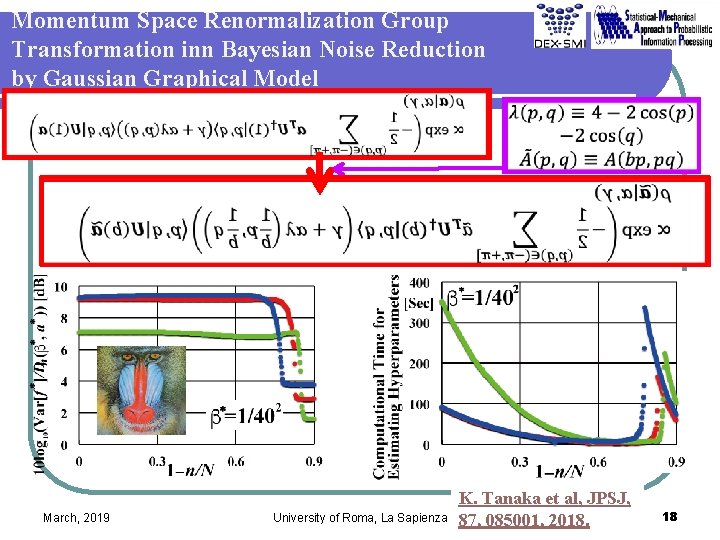
Momentum Space Renormalization Group Transformation inn Bayesian Noise Reduction by Gaussian Graphical Model March, 2019 University of Roma, La Sapienza K. Tanaka et al, JPSJ, 87, 085001, 2018. 18

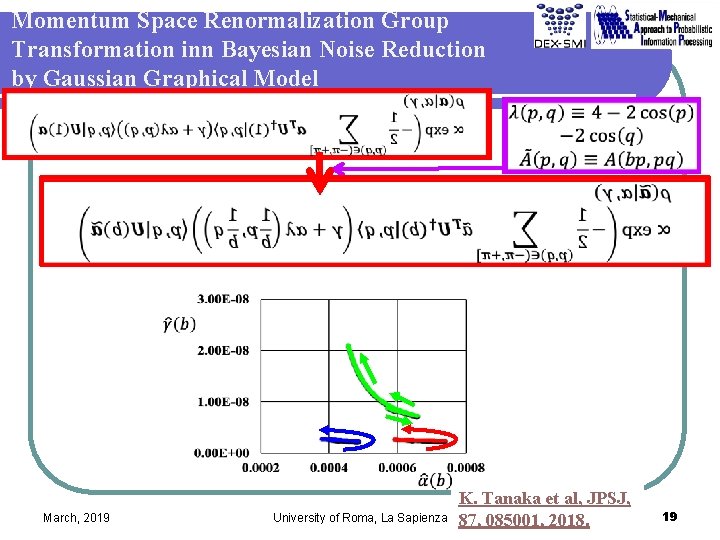
Momentum Space Renormalization Group Transformation inn Bayesian Noise Reduction by Gaussian Graphical Model March, 2019 University of Roma, La Sapienza K. Tanaka et al, JPSJ, 87, 085001, 2018. 19

Recent Development of Statistical Machine Learning Theory Model Selection from Big Data is the most important problem!! Maximum Likelihood Estimation It can be regarded as one of optimization problems!! We have many algorithms for continuous optimization problems. Problem is focused to how to treat untractable probabilistic modeling, particularly sparse modeling and discrete probabilistic modeling. • Markov Chain Monte Carlo Sampling and Simulated Annealing • Advanced Mean Field Method (Belief Propagation) • Quantum-Mechanical Monte Carlo Sampling and Quantum Annealing D-Wave Machine March, 2019 University of Roma, La Sapienza 20