Momentum The linear momentum of a particle is

Momentum The (linear) momentum of a particle is defined as the product of the particle's mass and velocity Momentum is a quantity describing the motion of the particle. p m v The relation between kinetic energy and momentum

Newton's second law II (modern version) In an inertial reference frame, the rate of change in the momentum of a particle is equal to the net force exerted on the particle classical (non-relativistic) version:

Impulse If an object interacts with a particle over a certain time interval (t 1, t 2), the integral is called the impulse. The average force over a certain time interval is directly related to the impulse of this force over this time interval

Impulse - Momentum theorem In an inertial reference frame, the change in the momentum of a particle is equal to the net impulse (impulse of the net force)

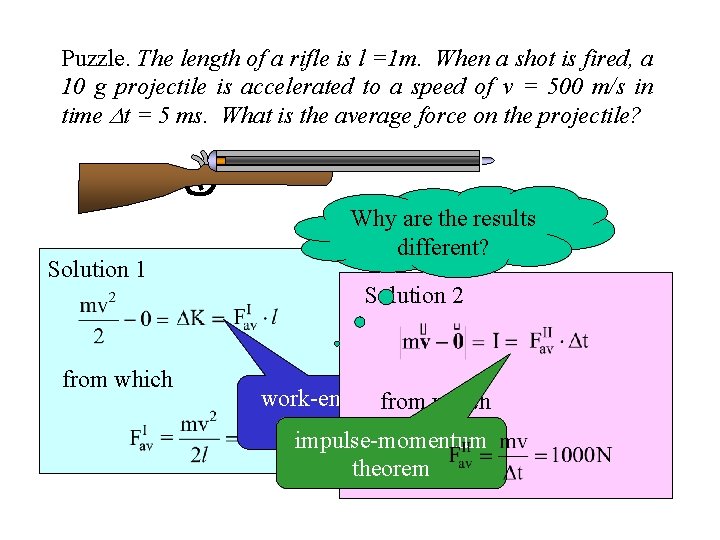
Puzzle. The length of a rifle is l =1 m. When a shot is fired, a 10 g projectile is accelerated to a speed of v = 500 m/s in time t = 5 ms. What is the average force on the projectile? Solution 1 from which Why are the results different? Solution 2 work-energyfrom which theorem impulse-momentum theorem

total value of a physical quantity (for a system of particles) If a certain physical quantity is defined for particles, we define the total of this physical quantity for a system of particles as the sum of the quantity over all the particles constituting the system. m 1 m 2 (total) mass of a system p 1 p 2 (total) momentum of a system (total) kinetic of a system m 3 p 3

Conservation of Momentum If a system of particles is isolated, the total momentum of the system is constant because

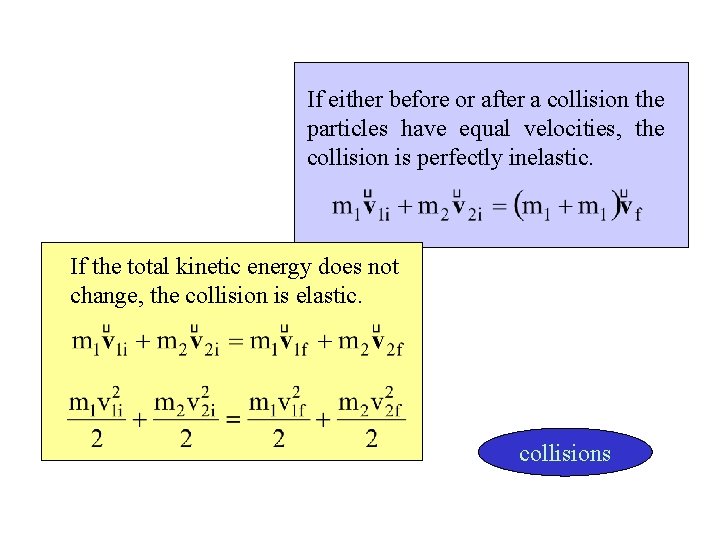
Collisions • • • inelastic (maximum loss in total kinetic energy) (no loss in total kinetic energy) Mechanical interactions between bodies over a finite time are called collisions. Collisions do not affect the total momentum of the system. In case an external force is applied but the collision takes voyagerof the place in a time period negligible for the effects external force, the external force can be ignored.

If either before or after a collision the particles have equal velocities, the collision is perfectly inelastic. If the total kinetic energy does not change, the collision is elastic. collisions

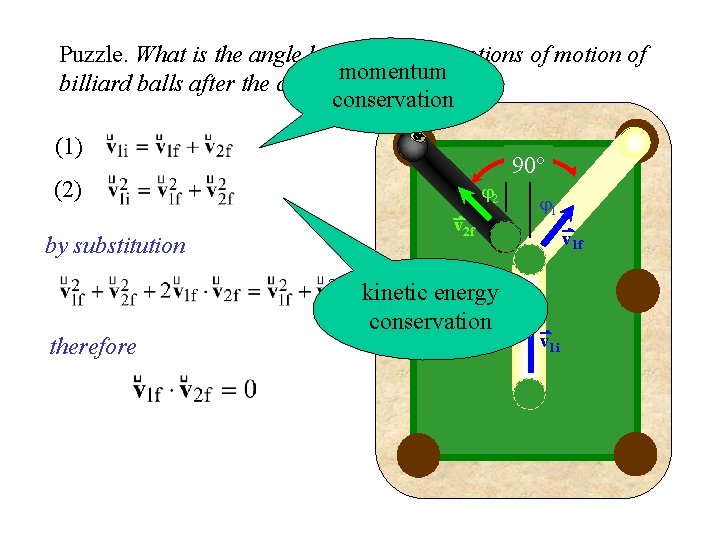
Puzzle. What is the angle between the directions of motion of momentum billiard balls after the collision ? conservation (1) 90° (2) by substitution therefore j 2 v 2 f kinetic energy conservation j 1 v 1 f v 1 i

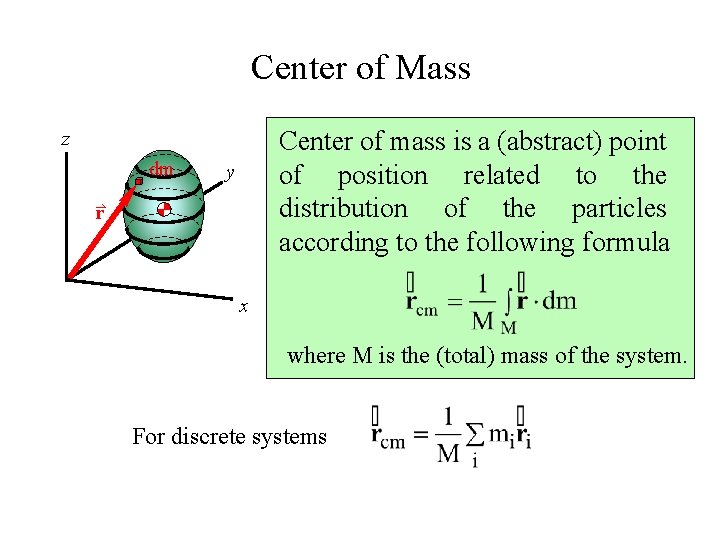
Center of Mass Center of mass is a (abstract) point of position related to the distribution of the particles according to the following formula z dm y r x where M is the (total) mass of the system. For discrete systems

Example. Three identical particles z [0, 0, 1] [0, 1, 0] y [1, 0, 0] x

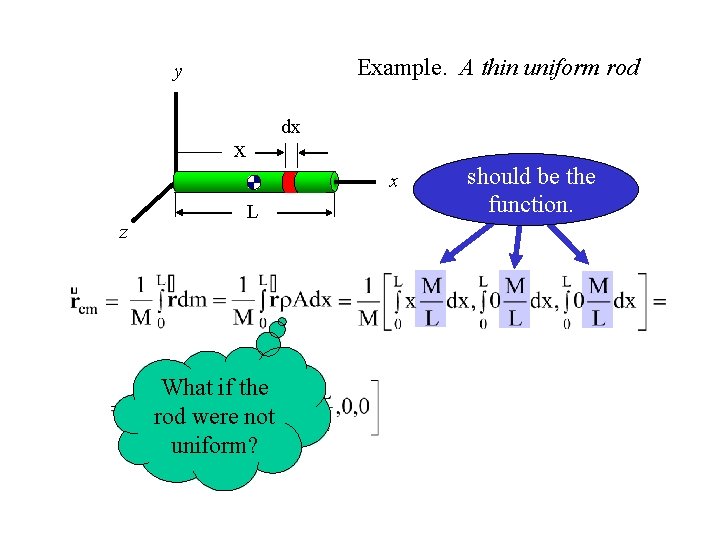
Example. A thin uniform rod y dx x x z L What if the rod were not uniform? should be the function.

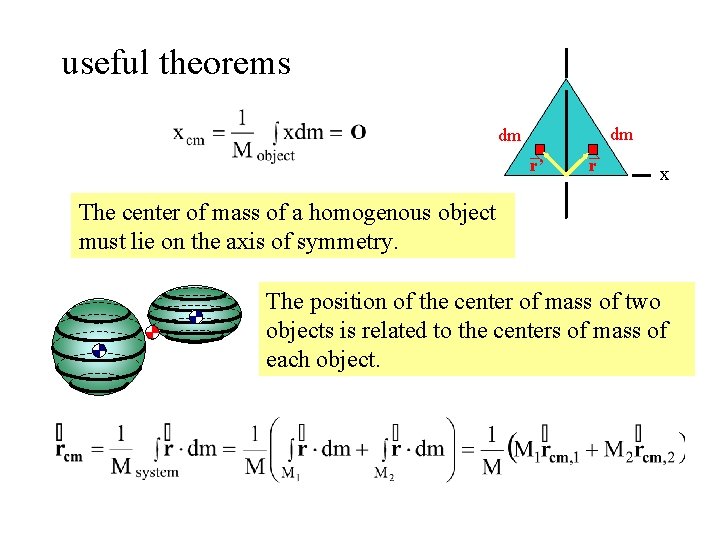
useful theorems dm dm r’ r x The center of mass of a homogenous object must lie on the axis of symmetry. The position of the center of mass of two objects is related to the centers of mass of each object.

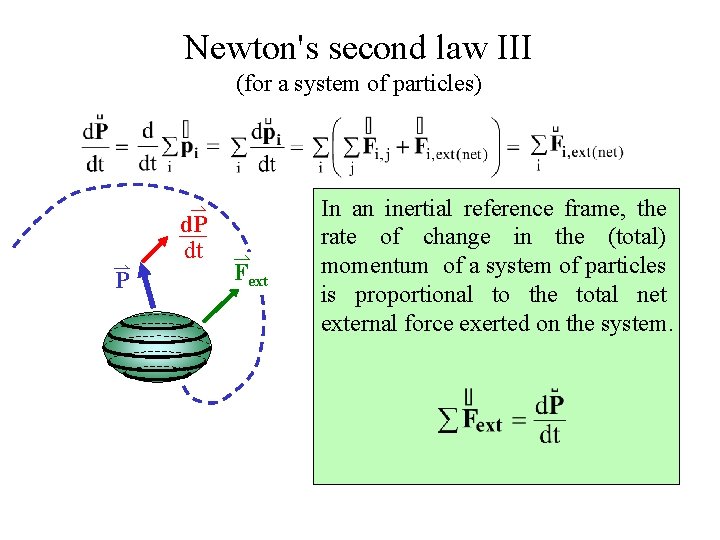
Newton's second law III (for a system of particles) d. P dt P Fext In an inertial reference frame, the rate of change in the (total) momentum of a system of particles is proportional to the total net external force exerted on the system.

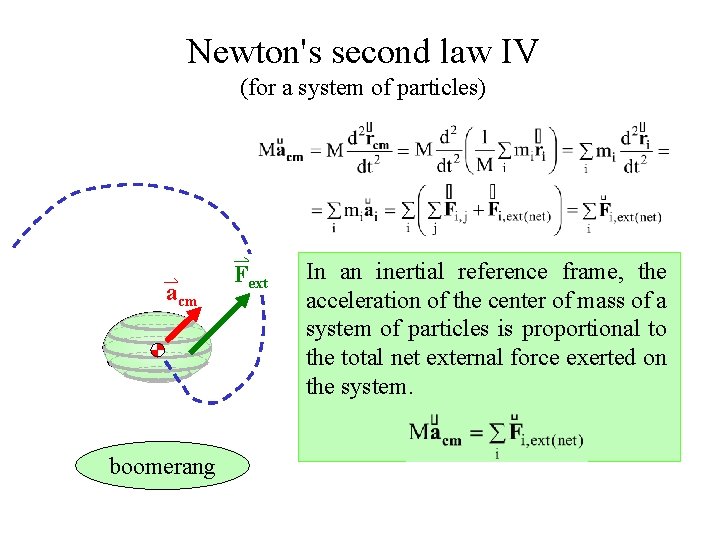
Newton's second law IV (for a system of particles) acm boomerang Fext In an inertial reference frame, the acceleration of the center of mass of a system of particles is proportional to the total net external force exerted on the system.

Total Momentum and the Center of Mass The (total) momentum of a system of particles is related to the velocity of the center of mass of the system. the Moon

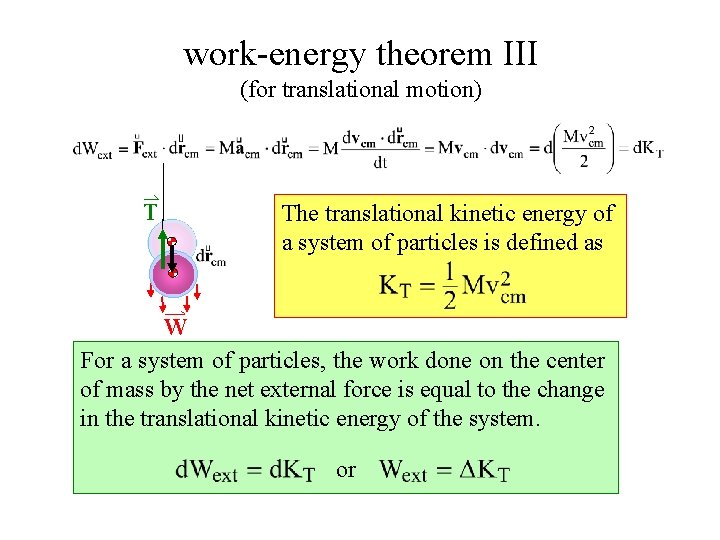
work-energy theorem III (for translational motion) T The translational kinetic energy of a system of particles is defined as W For a system of particles, the work done on the center of mass by the net external force is equal to the change in the translational kinetic energy of the system. or

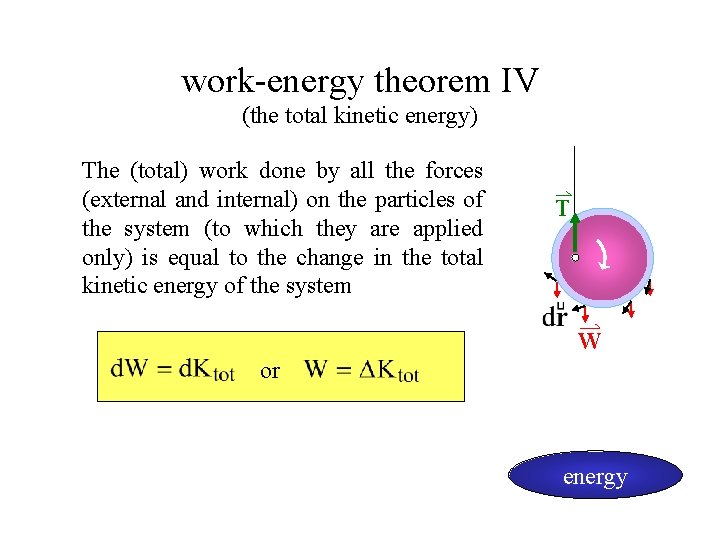
work-energy theorem IV (the total kinetic energy) The (total) work done by all the forces (external and internal) on the particles of the system (to which they are applied only) is equal to the change in the total kinetic energy of the system T W or energy

total gravitational potential energy (near the surface) U hcm U 0 = 0 Mghcm