Momentum Notes Momentum Mass x Velocity mv momentum

Momentum Notes

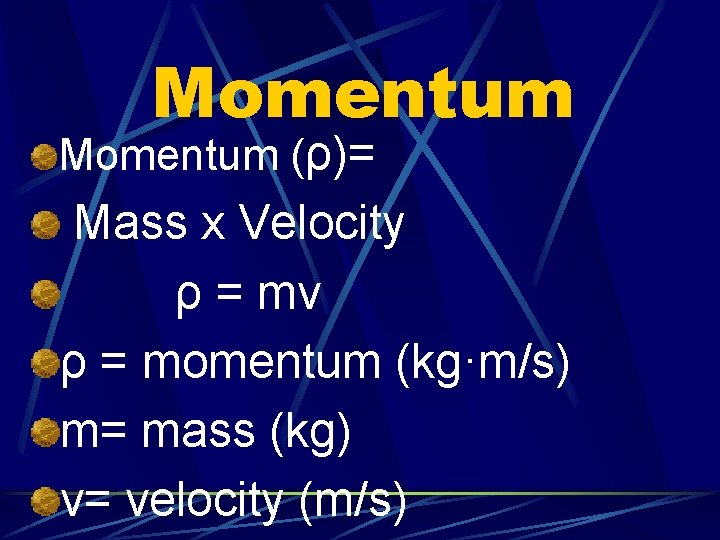
Momentum (ρ)= Mass x Velocity ρ = mv ρ = momentum (kg·m/s) m= mass (kg) v= velocity (m/s)

Momentum Linear momentum of an object of mass m moving with a velocity v is the product of the mass and velocity Inertia in motion

Law of Conservation of Momentum Law of conservation of momentum says that in the absence of an external force, the total momentum of a system remains unchanged.

Law of Conservation of Momentum – Continued 1) This law applies to a closed system (one where no mass is gained or lost)

Law of Conservation of Momentum – Continued Momentum conserved if: l 2) At all times, only two objects are involved l 3) The only forces involved are internal

Impulse I=Ft I= impulse (N*s) F=force (N) t= time (s) Also Ft=mv 2 -mv 1 F=Force (N) m=mass (kg) v=velocity (m/s)

Impulses Product of the average net force exerted on an object and the time interval over which the force acts. F • t = impulse (I) Impulses are measured in N • s

Impulse/Momentum Theorem Impulse of an object is equal to the change in momentum it causes F • t = mv 2 – mv 1

Impulse If you extend the time of impact you reduce the amount of force.

Types of Collisions Elastic Collisions – when objects collide without being permanently deformed and without generating heat l. Ex: Billiard balls colliding

Elastic Collisions m 1 v 1 + m 2 v 2 = m 1 v 1 + m 2 v 2 st m 1=mass of 1 object (kg) v 1=velocity of 1 st object(m/s) m 2= mass of 2 nd object(kg) nd v 2=velocity of 2 object(m/s)

Types of Collisions Inelastic Collisions – whenever colliding objects become tangled or couple together l. Ex: Two freight train cars hitting and continuing

Inelastic Collision m 1 v 1 + m 2 v 2 = mtotalvtotal m 1=mass of 1 st object (kg) v 1=velocity of 1 st object(m/s) m 2= mass of 2 nd object(kg) v 2=velocity of 2 nd object(m/s) mtot= 1 st and 2 nd mass added vtot= final velocity of both

Calculations momentum before collision = momentum after collision ρbefore = ρafter ρ 1 + ρ 2= ρ 1 + ρ 2