Momentum Impulse Topic 2 2 Momentum When have

Momentum & Impulse Topic 2. 2

Momentum � When have you heard this term? Some examples: � The Maple Leafs have won 5 straight games and they are building momentum towards the playoffs � The momentum to use technology has been huge in the past few years � Keeping your momentum is the key to reaching yearly resolutions

Momentum � What makes an object hard to stop? � Is it harder to stop a bullet, or a truck travelling along the highway? � What makes each object hard to stop?

Momentum � The bullet is hard to stop because it is travelling very fast, whereas the truck is hard to stop because it has a very large mass.

Momentum � It makes sense to assume that a bullet travelling twice as fast would be twice as hard to stop, and a truck twice the mass would also be twice as hard to stop.

Momentum � Momentum is a useful quantity to consider when thinking about "unstoppability". It is also useful when considering collisions and explosions. It is defined as Momentum (kg. m. s-1) = Mass (kg) x Velocity (m. s-1) p = mv

An easy example �A truck has a mass of 10 000 kg and a velocity of 3 m. s-1. What is its momentum? Momentum = Mass x velocity = 10 000 x 3 = 30 000 kg. m. s-1.

Linear Momentum momentum p of a body of constant mass m moving with velocity v is, by definition mv � The �p = mv � It is a vector quantity � Its units are kg m s-1 or Ns � It is the property of a moving body.

Conservation of momentum 1. In a collision between two objects, momentum is conserved (total momentum stays the same) 2. In an isolated system (no outside forces), momentum remains constant isolated system = translational equilibrium We can use this to calculate what happens after a collision (and in fact during an “explosion”). Momentum is not energy!

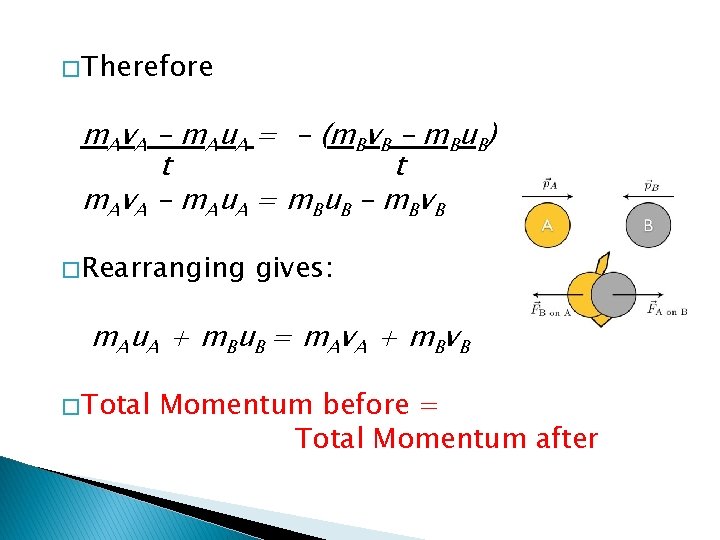
Deriving This Law � To derive this law we apply Newton´s 2 nd law to each body and Newton´s 3 rd law to the system Imagine 2 bodies A and B interacting � mass of m. A and m. B � A has a velocity change of u. A to v. A and B has a velocity change of u. B to v. B during the time of the interaction t � i. e.

� Then � FA = m. Av. A – m. Au. A � And � FB the force on A given by Newton 2 is t the force on B is = m Bv B – m Bu B � But t Newton 3 says that these 2 forces are equal in magnitude and opposite in direction

� Therefore m. Av. A – m. Au. A = - (m. Bv. B – m. Bu. B) t t m A v A – m A u A = m Bu B – m Bv B � Rearranging gives: m A u A + m Bu B = m A v A + m Bv B � Total Momentum before = Total Momentum after

A harder example! � A car of mass 1000 kg travelling at 5 m. s-1 hits a stationary truck of mass 2000 kg. After the collision they stick together. What is their joint velocity after the collision? � What does ‘joint velocity’ mean? � What ELSE does it mean?

A harder example! Before 1000 kg 2000 kg 5 m. s-1 Momentum before = 1000 x 5 + 2000 x 0 = 5000 kg. m. s-1 After Combined mass = 3000 kg V m. s-1 Momentum after = 3000 v

A harder example The law of conservation of momentum tells us that momentum before equals momentum after, so p 1 total= p 2 total 5000 = 3000 v V = 5000/3000 = 1. 67 m. s-1

Momentum is a vector � Momentum is a vector, so if velocities are in opposite directions we must take this into account in our calculations

An even harder example! Snoopy (mass 10 kg) running at 4. 5 m. s-1 jumps onto a skateboard of mass 4 kg travelling in the opposite direction at 7 m. s-1 What is the velocity of Snoopy and skateboard after Snoopy has jumped on? I love physics

An even harder example! Because they are in opposite directions, we make one velocity negative 10 kg -4. 5 m. s-1 7 m. s-1 4 kg Momentum before = 10 x -4. 5 + 4 x 7 = -45 + 28 = -17 14 kg v m. s-1 Momentum after = 14 v

An even harder example! Momentum before = Momentum after -17 = 14 v V = -17/14 = -1. 21 m. s-1 The negative sign tells us that the velocity is from left to right (we choose this as our “negative direction”)

Newton´s Second Law Revisited �F = ma �F = mv – mu t � The F=mv - mu t t F = p t rate of change of momentum of a body is proportional to the resultant force and occurs in the direction of the force.

Impulse � Where have you heard this term? Some Examples: � I bought that from the internet on impulse after seeing the commercial on TV � I got into a fight on impulse after being called a name

Impulse F = p F = mv – mu t t Ft = mv – mu = p � � quantity Ft is called the impulse of the force on the body � This � It is a vector quantity � Its units are kg m s-1 or Ns

Impulse � Ft � The = mv – mu = p quantity Ft is called the impulse, and mv – mu is the change in momentum � (v = final velocity and u = initial velocity) � Impulse = Change in momentum

Units Impulse is measured in N. s (Ft) or [kg. m. s-2]x[s] = [kg. m. s-1] (mv – mu)

Impulse � Note: For a ball (mass m) bouncing off a wall, don’t forget the initial and final velocity are in different directions, so you will have to make one of them negative. � In this case mv – mu = 5 m – (-3 m) = 8 m 5 m/s -3 m/s

Example � Dylan punches Joseph in the face. If Joseph’s head (mass 10. 0 kg) was initially at rest and moves away from Dylan’s fist at 3. 0 m/s, and the fist was in contact with the face for 0. 20 seconds, what was the force of the punch? � m = 10. 0 kg, t = 0. 20 s, u = 0, v = 3. 0 m/s � Ft = mv – mu � 0. 2 F = 10 x 3 – 10 x 0 � 0. 2 F = 30 � F = 30/0. 2 = 150 N

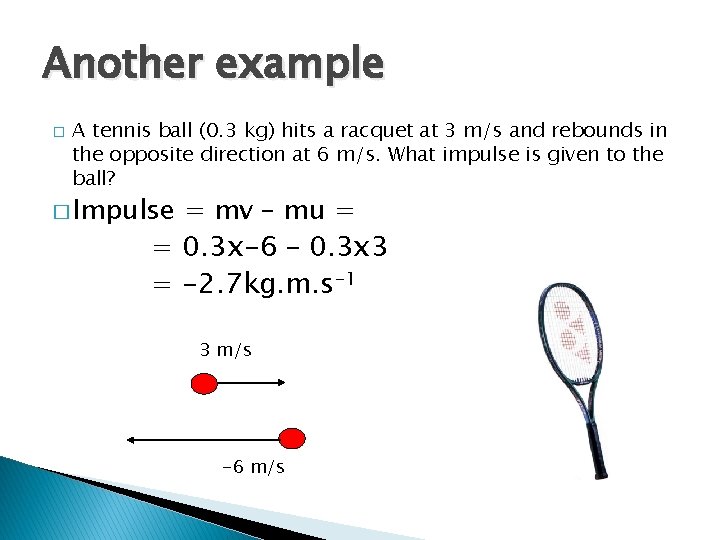
Another example �A tennis ball (0. 3 kg) hits a racquet at 3 m/s and rebounds in the opposite direction at 6 m/s. What impulse is given to the ball?

Another example �A tennis ball (0. 3 kg) hits a racquet at 3 m/s and rebounds in the opposite direction at 6 m/s. What impulse is given to the ball? 3 m/s -6 m/s

Another example � A tennis ball (0. 3 kg) hits a racquet at 3 m/s and rebounds in the opposite direction at 6 m/s. What impulse is given to the ball? � Impulse = mv – mu = = 0. 3 x-6 – 0. 3 x 3 = -2. 7 kg. m. s-1 3 m/s -6 m/s