Momentum Impulse and Projectile Motion Momentum What is

Momentum & Impulse and Projectile Motion

Momentum What is momentum? It is the quantity of motion of a moving body, measured as a product of its mass and velocity. Think of it as inertia in motion.

Wasting time with videos : D http: //www. youtube. com/watch? v=e 1 IJUNW 7 Kq 4

Calculation of momentum To calculate for momentum: momentum = mass x velocity p = mv

An 10 kg object moving at a velocity of 3 m/s has a momentum of p = mv p = 10 * 3 p = 30 kg m/s = 30 Ns (Newton second)

Impulse What is impulse? It is the change in momentum.

Two ways to determine impulse. Dp = m. Dv change of momentum = mass x change in velocity Or Dp = FDt change of momentum = force x change in time

An 10 kg object change velocity from 3 m/s to 10 m/s has an impulse of impulse = 10 * (10 -3) = 70 Ns

How?

A 100 Kg man is running at 5. 6 m/s. What is his momentum? p = 100 * 5. 6 = 560 Ns (600 Ns)

How fast is a 1. 50 kg ball moving if it has a momentum of 4. 50 kg·m/s? p = mv 4. 50 Ns = 1. 50 * v v = 4. 50/1. 50 = 3. 00 m/s

A net force of 100 Newton’s is applied to a wagon for 5 seconds. This causes the wagon to undergo an impulse of? Dp = FDt Dp = 100 * 5 = 500 Ns

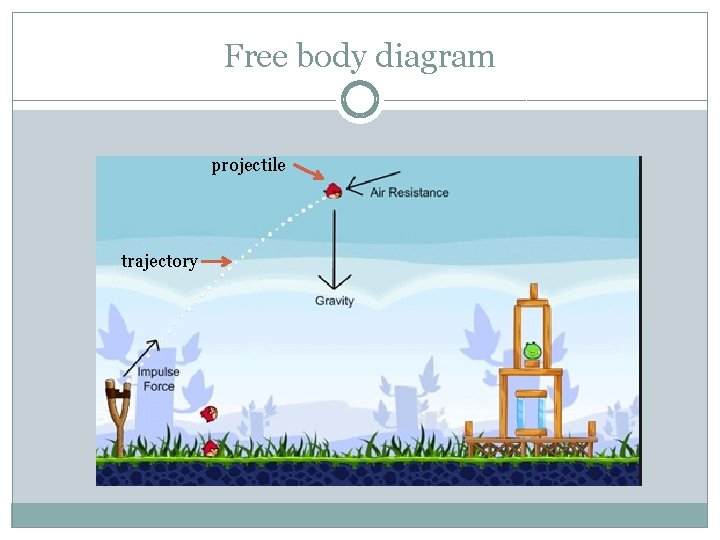
projectile What is a projectile? A projectile is any object that moves through the air or space, acted on only by gravity (and air resistance, if any). Examples: A cannonball shot from a cannon, a stone thrown into the air, a ball rolling off the edge of a table, a spacecraft circling Earth

Free body diagram projectile trajectory

equations Horizontal displacement: x = vx t x = horizontal displacement vx = horizontal velocity t = time

Vertical displacement: y = h 0 + vi t + ½ at 2 y = vertical displacement h 0 = original position (height) vi = initial velocity a = acceleration (due to gravity, g) t = time

Other equations vf = final velocity vi = initial velocity d = displacement a = acceleration t = time

There are only three types of problems that have to do with projectile motion. Type I: Finding out where an object landed after falling from a given height with some initial velocity. To solve this: 1 st determine how long it takes the object to hit the ground. 2 nd use the horizontal displacement equation with the calculated time along with the initial velocity to determine the displacement.

Type II: Object is thrown into the air with an initial velocity from some height and you are asked to determine the a. the height of the object b. time it took for the object to hit the ground, To solve 1 st use the final velocity equation (vf = vi + at) to determine the time the object reached its peak. 2 nd use the vertical displacement equation and the calculated time to determine the height.

b. Using the height from part a, we can use the equation where d is the height the object reached. Add this time to the time from part a to get the total time.

Type III A combination of type I and type II.

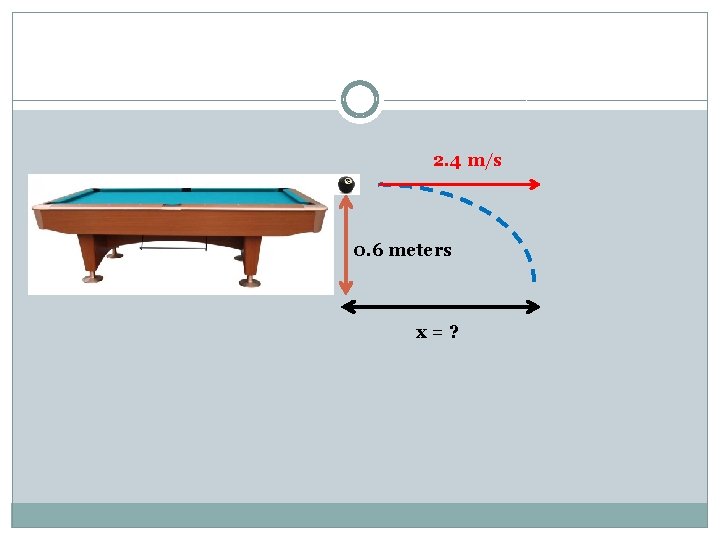
Example 1 A pool ball leaves a 0. 60 -meter high table with an initial horizontal velocity of 2. 4 m/s. Predict the time required for the pool ball to fall to the ground and the horizontal distance between the table's edge and the ball's landing location.

2. 4 m/s 0. 6 meters x=?

Step 1: determine how long it takes to hit the ground by using the equation d = vit + ½ at 2 the initial vertical velocity is 0 m/s which makes the equation d = ½ at 2 solving for time from this equation we get using d = 0. 6 meters and a = 9. 8 m/s 2 This is how long it will take for the ball to hit the ground

Step 2: Using the time found in step 1 and the equation for the horizontal displacement, we can determine where the ball will land. x = vx t vx was given as 2. 4 m/s t was calculated to be 0. 35 sec. Therefore x = 2. 4 * 0. 35 = 0. 84 meters The ball will land 0. 84 meters from the edge of the table.

A soccer ball is kicked horizontally off a 22. 0 -meter high hill and lands a distance of 35. 0 meters from the edge of the hill. Determine the initial horizontal velocity of the soccer ball. 22 m 35 m

With this example, we can again use the equation we found from the last problem to solve for time. Height was given as 22 meters, so it will take 2. 1 seconds for the ball to hit the bottom of the cliff.

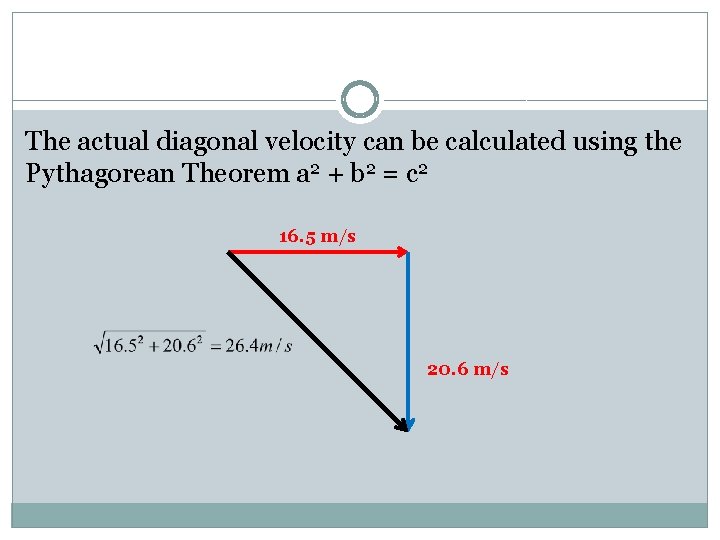
Using the horizontal displacement equation we can determine how fast it was moving. x = vx * t x = horizontal displacement x = 35 meters t = 2. 1 seconds 35 = vx * (2. 1) vx = 35 / 2. 1 = 16. 5 m/s (17 m/s)

We can also determine how fast vertical it was traveling before it hit the ground (vertical velocity). To do this we need to use the equation vf = vi + at. The a is 9. 8 m/s 2 and the vi = 0 m/s vf = 0 + 9. 8 (2. 1) = 20. 58 (21 m/s)

The actual diagonal velocity can be calculated using the Pythagorean Theorem a 2 + b 2 = c 2 16. 5 m/s 20. 6 m/s