Moments of Random Variables The moment generating function

Examples 1. The Binomial distribution (parameters p, n) 2. The Poisson distribution (parameter l)

3. The Exponential distribution (parameter l) 4. The Standard Normal distribution (m = 0, s = 1)

5. The Gamma distribution (parameters a, l) 6. The Chi-square distribution (degrees of freedom n) (a = n/2, l = 1/2)

Properties of Moment Generating Functions 1. m. X(0) = 1

The log of Moment Generating Functions Let l. X (t) = ln m. X(t) = the log of the moment generating function

Thus l. X (t) = ln m. X(t) is very useful for calculating the mean and variance of a random variable

Examples 1. The Binomial distribution (parameters p, n)

2. The Poisson distribution (parameter l)

3. The Exponential distribution (parameter l)

4. The Standard Normal distribution (m = 0, s = 1)

5. The Gamma distribution (parameters a, l)

6. The Chi-square distribution (degrees of freedom n)

Jointly distributed Random variables Multivariate distributions

Discrete Random Variables

The joint probability function; p(x, y) = P[X = x, Y = y]

Marginal distributions Conditional distributions

Continuous Random Variables

Definition: Two random variable are said to have joint probability density function f(x, y) if

Marginal distributions Conditional distributions

Independence

Definition: Two random variables X and Y are defined to be independent if if X and Y are discrete if X and Y are continuous Thus in the case of independence marginal distributions ≡ conditional distributions

The Multiplicative Rule for densities if X and Y are discrete if X and Y are continuous

Proof: This follows from the definition for conditional densities: Hence and The same is true for continuous random variables.

Example: Suppose that a rectangle is constructed by first choosing its length, X and then choosing its width Y. Its length X is selected form an exponential distribution with mean m = 1/l = 5. Once the length has been chosen its width, Y, is selected from a uniform distribution form 0 to half its length. Find the probability that its area A = XY is less than 4.

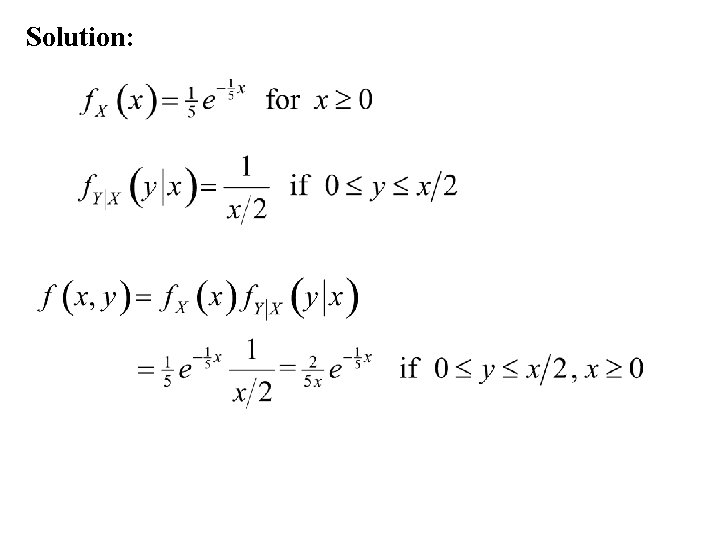
Solution:

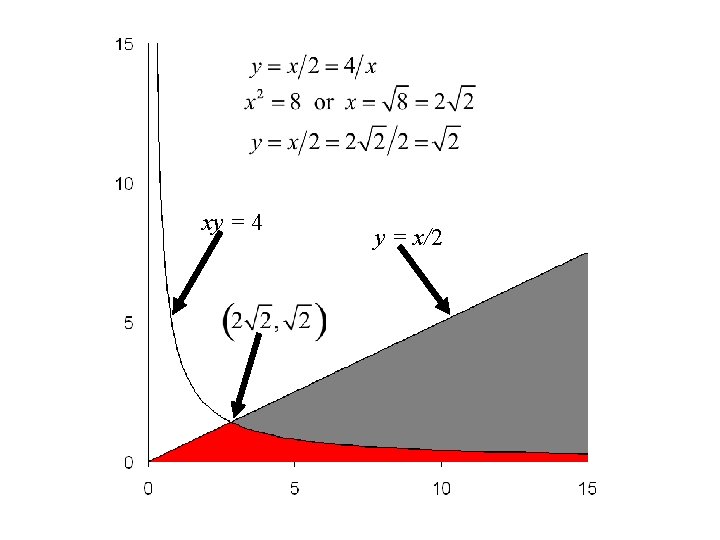
xy = 4 y = x/2

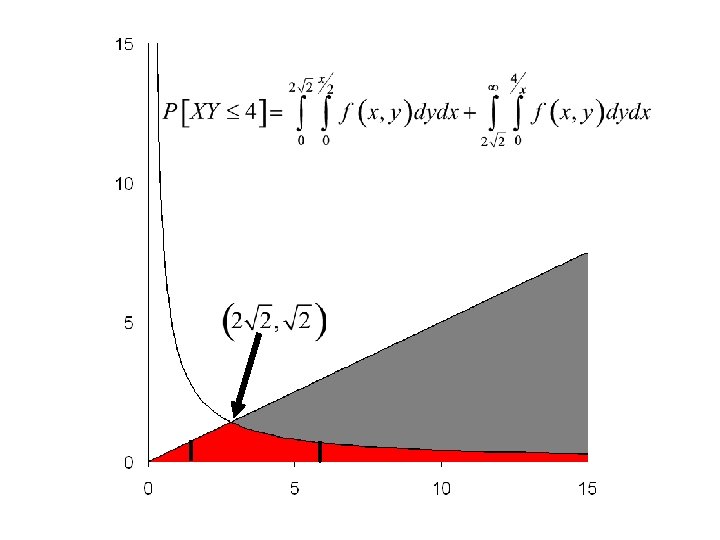
This part can be evaluated This part may require Numerical evaluation