Moments At an angle KUS objectives BAT solve

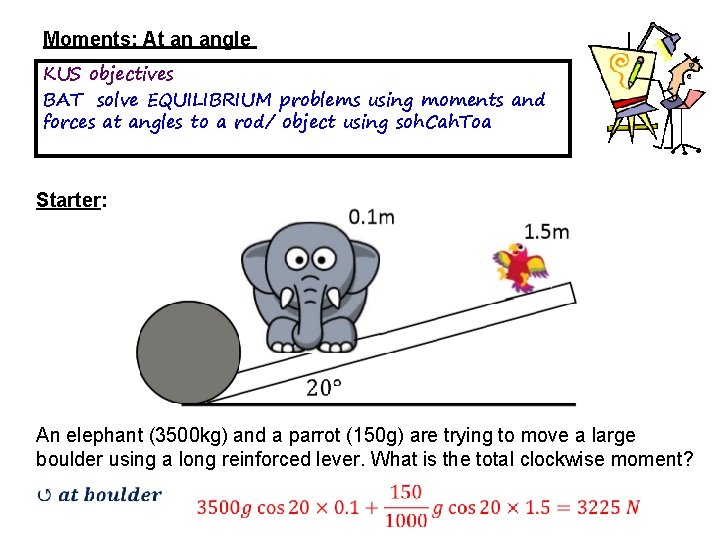
Moments: At an angle KUS objectives BAT solve EQUILIBRIUM problems using moments and forces at angles to a rod/ object using soh. Cah. Toa Starter: An elephant (3500 kg) and a parrot (150 g) are trying to move a large boulder using a long reinforced lever. What is the total clockwise moment?

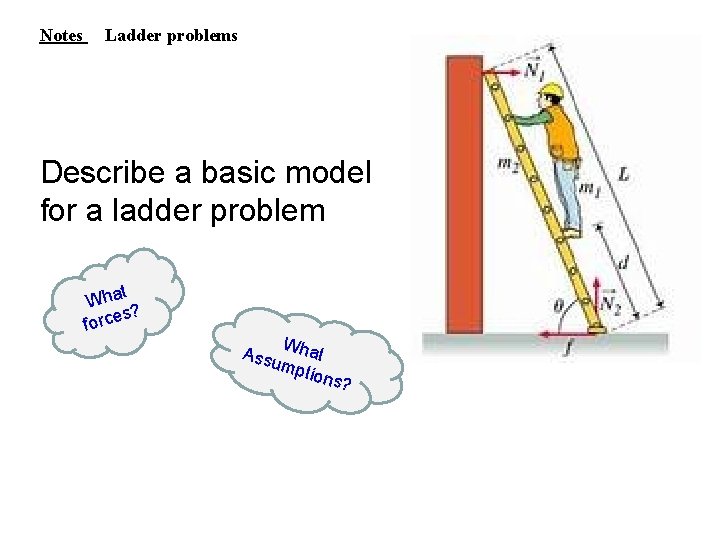
Notes Ladder problems Describe a basic model for a ladder problem t Wha s? force Wha t mpti on Assu s?

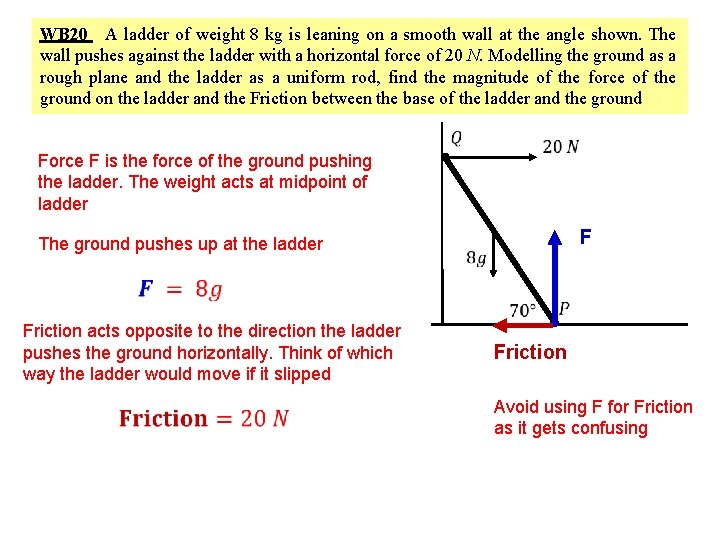
WB 20 A ladder of weight 8 kg is leaning on a smooth wall at the angle shown. The wall pushes against the ladder with a horizontal force of 20 N. Modelling the ground as a rough plane and the ladder as a uniform rod, find the magnitude of the force of the ground on the ladder and the Friction between the base of the ladder and the ground Force F is the force of the ground pushing the ladder. The weight acts at midpoint of ladder F The ground pushes up at the ladder Friction acts opposite to the direction the ladder pushes the ground horizontally. Think of which way the ladder would move if it slipped Friction Avoid using F for Friction as it gets confusing

WB 21 A uniform rod PQ is hinged at point P, and is held in equilibrium at an angle of 50 to the horizontal by a force of magnitude F acting perpendicular to the rod at Q. Given that the rod has a length of 3 m and mass of 8 kg, find the value of F Taking moments about P

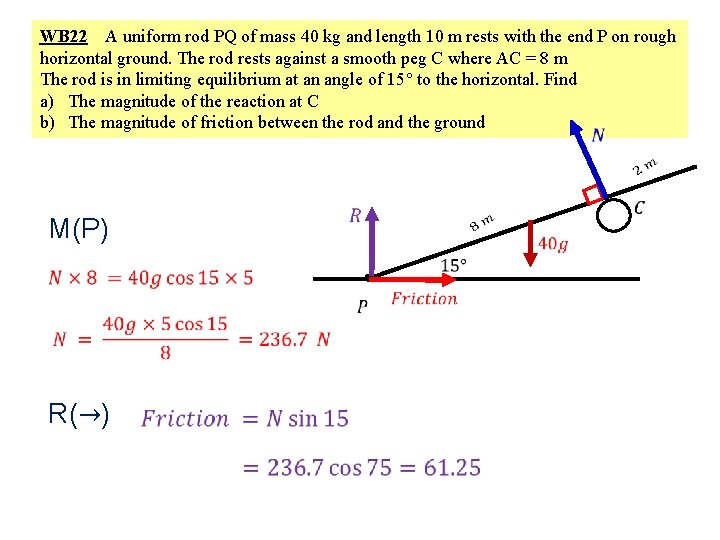
WB 22 A uniform rod PQ of mass 40 kg and length 10 m rests with the end P on rough horizontal ground. The rod rests against a smooth peg C where AC = 8 m The rod is in limiting equilibrium at an angle of 15 to the horizontal. Find a) The magnitude of the reaction at C b) The magnitude of friction between the rod and the ground M(P) R(→)

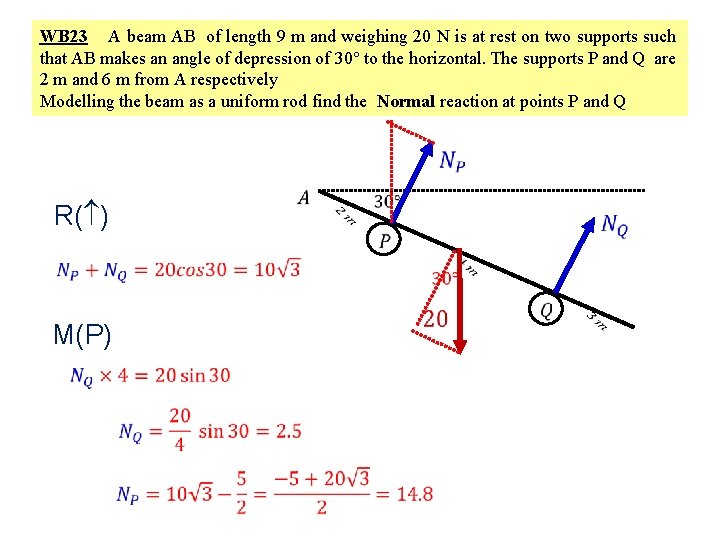
WB 23 A beam AB of length 9 m and weighing 20 N is at rest on two supports such that AB makes an angle of depression of 30 to the horizontal. The supports P and Q are 2 m and 6 m from A respectively Modelling the beam as a uniform rod find the Normal reaction at points P and Q R( ) M(P)

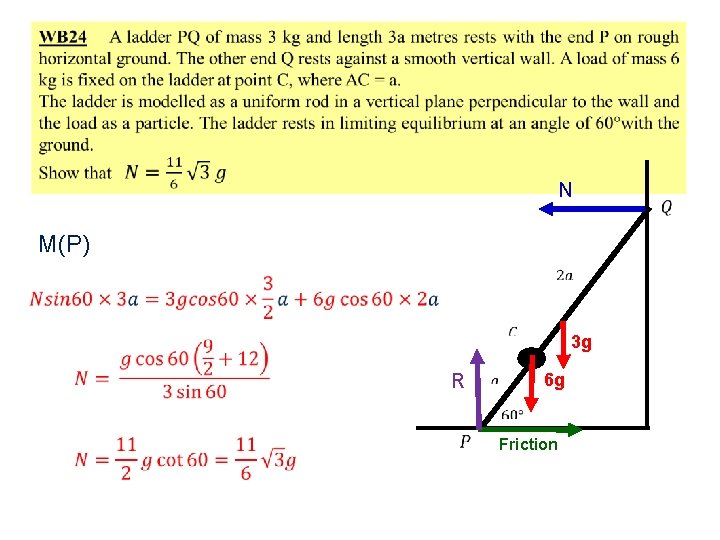
N M(P) 3 g R 6 g Friction

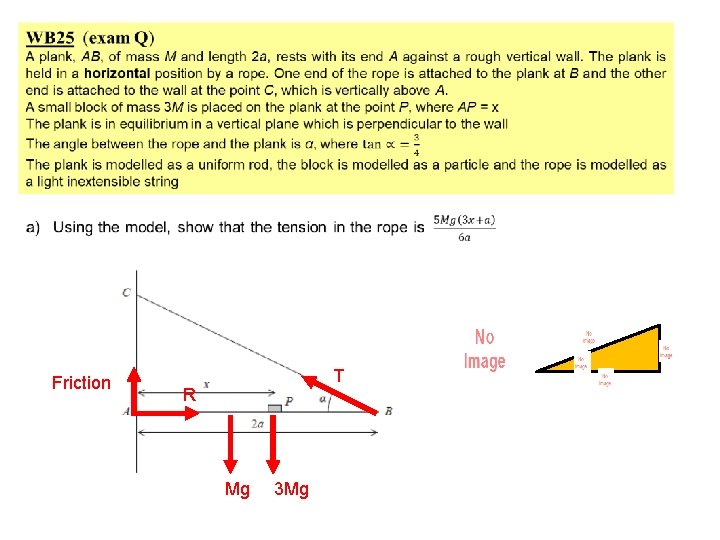
Friction T R Mg 3 Mg

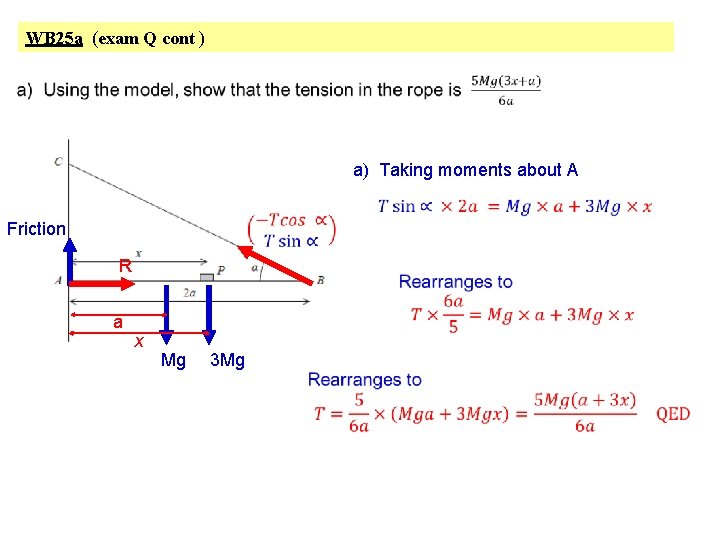
WB 25 a (exam Q cont ) a) Taking moments about A Friction R a x Mg 3 Mg

WB 25 b (exam Q cont ) The magnitude of the horizontal component of the force exerted on the plank at A by the wall is 2 Mg Find x in terms of a b) Horizontally forces are in equilibrium Friction Substituting result from a) gives R=2 Mg a x Mg 3 Mg

WB 25 c (exam Q cont ) c) Resolve forces vertically Friction R=2 Mg a x Mg Now find tan R=2 Mg 3 Mg

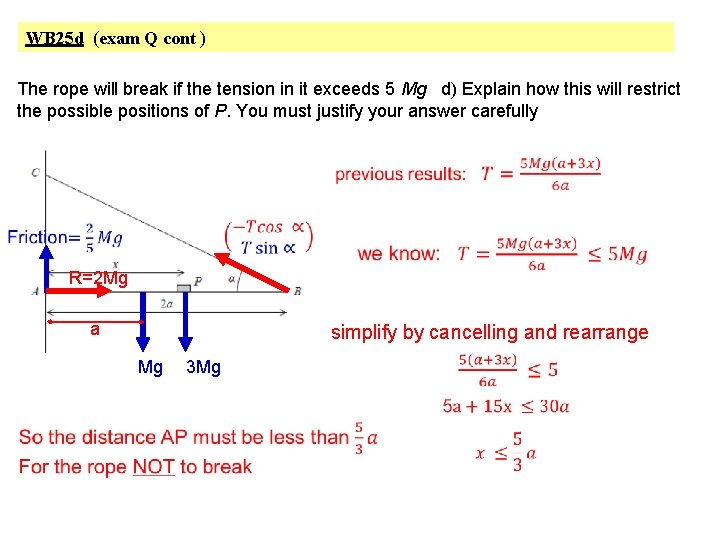
WB 25 d (exam Q cont ) The rope will break if the tension in it exceeds 5 Mg d) Explain how this will restrict the possible positions of P. You must justify your answer carefully R=2 Mg a simplify by cancelling and rearrange Mg 3 Mg

KUS objectives BAT solve equilibrium problems using moments and friction at angles to a rod/ object using soh. Cah. Toa self-assess One thing learned is – One thing to improve is –

END