Moment of Inertia and Rotational Dynamics The study











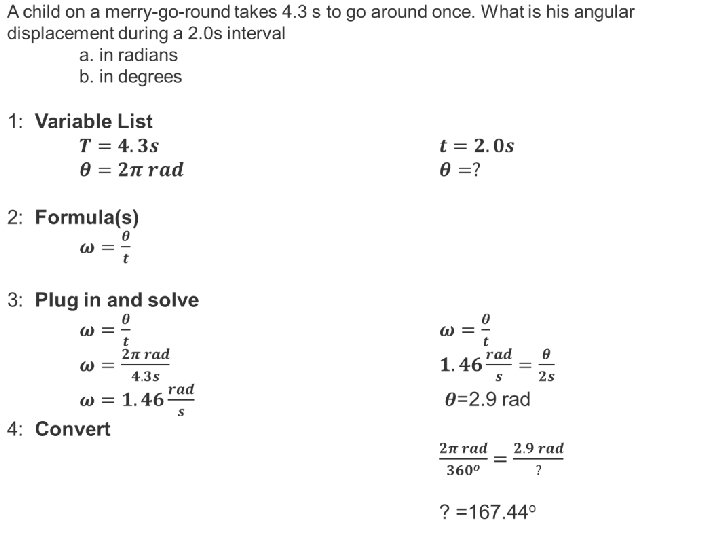






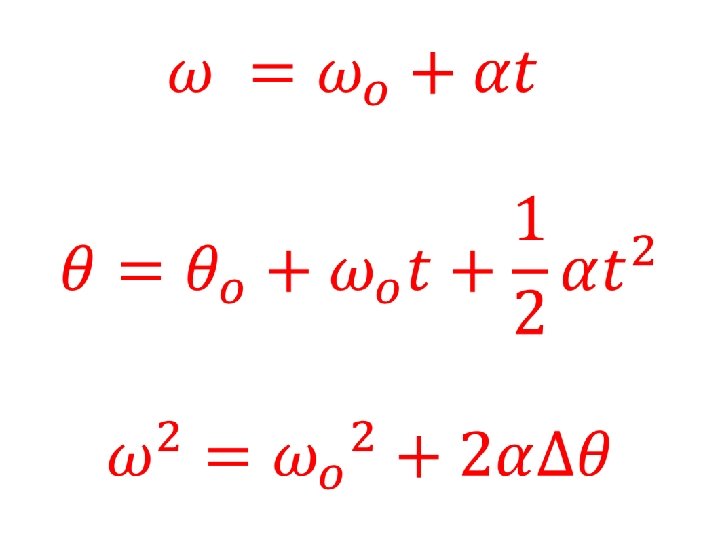


































- Slides: 78

Moment of Inertia and Rotational Dynamics The study of objects that are spinning

• WATCH YOUR UNITS – Radians – Degrees – Rotations – Seconds – Minutes – Hours 2π rad = 360 o = 1 rotation 1 hour = 60 minutes = 3600 seconds

Angular Position/Displacement

Translating from Linear Motion to Rotational Motion Linear • Position – Where you are relative to the origin. – Defined by x and y coordinates (measured in meters). – Right and up are usually positive – Down and left are usually negative Rotational • Angular Position – Where you are relative to the origin – Defined by r (distance from the center of a circle in meters) and θ the angle from the +x-axis (measured in radians) – The counter clockwise direction is positive! Conversion from Linear to Rotational 1 revolution = 360 degrees = 2π radians

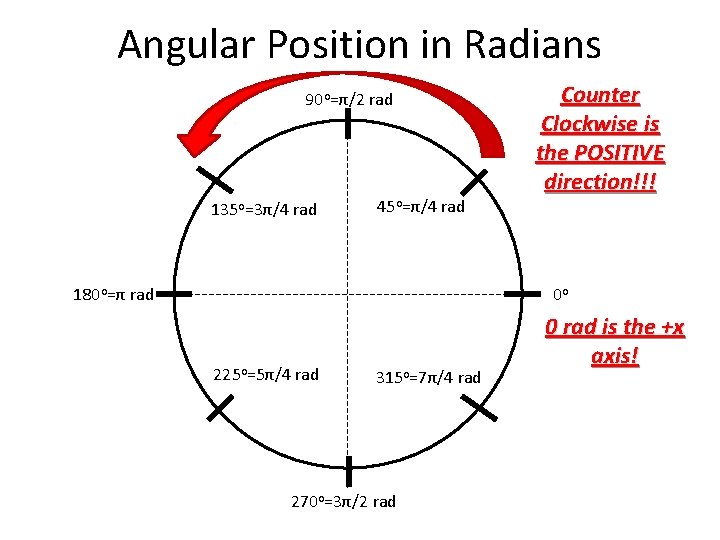
Angular Position in Radians 90 o=π/2 rad 135 o=3π/4 rad 45 o=π/4 rad 180 o=π rad Counter Clockwise is the POSITIVE direction!!! 0 o 225 o=5π/4 rad 315 o=7π/4 rad 270 o=3π/2 rad 0 rad is the +x axis!

Angular Position on a Clock Face Label each hour with the correct angular position measured in radians π/2 rad 2π/3 rad π/6 rad 5π/6 rad π rad 0 rad 11π/6 rad 7π/6 rad 4π/3 rad 3π/2 rad 5π/3 rad

Translating from Linear Motion to Rotational Motion Linear • Distance – the actual length of the path you follow “Arc length” • measured in meters • Symbol s Rotational •

Angular Speed/Velocity

• Recall…

Translating from Linear Motion to Rotational Motion Linear • Rotational •

Two children are riding on a spinning ride. The boy sits close to the center while the girl sits near the outer edge. 1. Compared to the boy’s period of motion, the period of the girl is… a. Greater 2. c. The same Compared to the angular velocity of the boy, the angular velocity of the girl is… a. Greater 3. b. Less c. The same Compared to the tangential velocity of the boy, the tangential velocity of the girl is… a. Greater b. Less c. The same

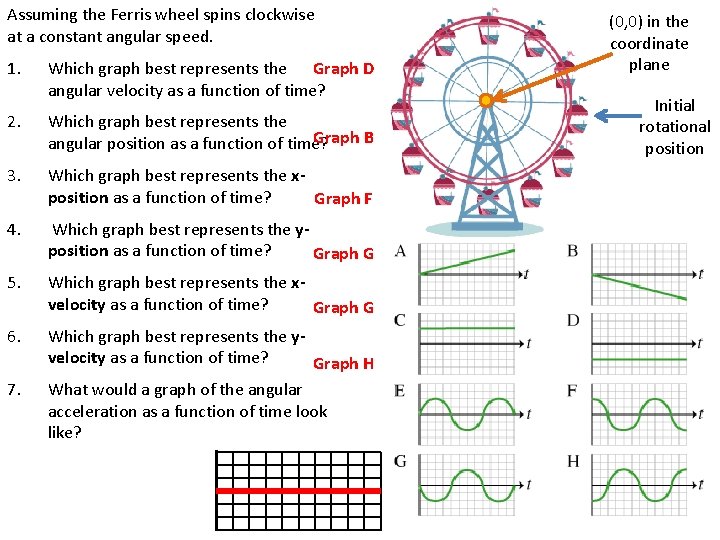
Assuming the Ferris wheel spins clockwise at a constant angular speed. 1. Which graph best represents the Graph D angular velocity as a function of time? 2. Which graph best represents the Graph B angular position as a function of time? 3. Which graph best represents the xposition as a function of time? Graph F 4. Which graph best represents the yposition as a function of time? Graph G 5. Which graph best represents the xvelocity as a function of time? Graph G 6. Which graph best represents the yvelocity as a function of time? Graph H What would a graph of the angular acceleration as a function of time look like? 7. (0, 0) in the coordinate plane Initial rotational position

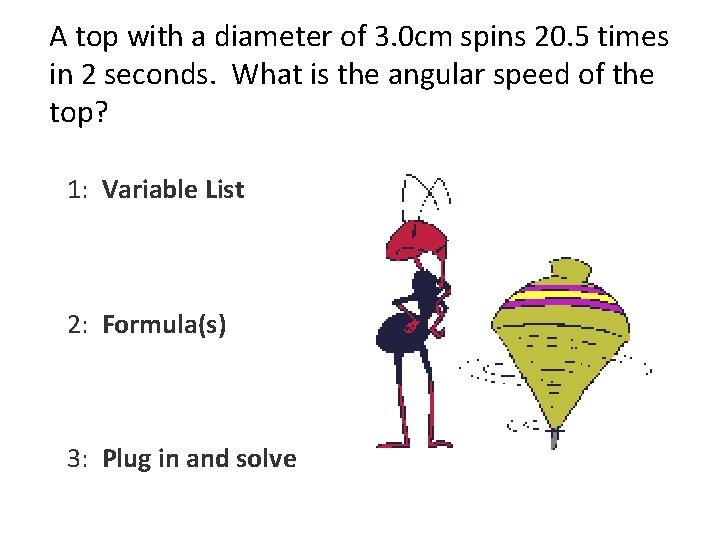
A top with a diameter of 3. 0 cm spins 20. 5 times in 2 seconds. What is the angular speed of the top? 1: Variable List 2: Formula(s) 3: Plug in and solve

A top with a diameter of 3. 0 cm spins 20. 5 times in 2 seconds. What is the angular speed of the top?

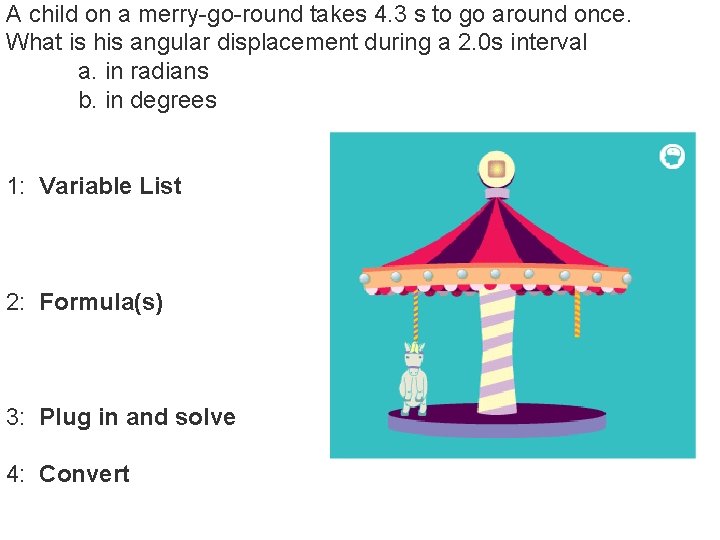
A child on a merry-go-round takes 4. 3 s to go around once. What is his angular displacement during a 2. 0 s interval a. in radians b. in degrees 1: Variable List 2: Formula(s) 3: Plug in and solve 4: Convert

At t=0 seconds, your friend is at the very bottom of the Ferris wheel. If the ride rotates at 0. 04 rad/seconds, where is your friend relative to his starting position after riding for 3 minutes? A. Answer in radians (between 0 and 2π) B. Answer in degrees (between 0 and 360)


A planet’s radius is 6000 miles. Two cities are located along the equator and are 7500 miles apart. a. What is the angular displacement between them? b. If it takes 7 hours to fly from one city to the other, what is the plane’s angular speed?

A planet’s radius is 6000 miles. Two cities are located along the equator and are 7500 miles apart. A. What is the angular displacement between them? B. If it takes 7 hours to fly from one city to the other, what is the plane’s angular speed?

Angular Acceleration

Translating from Linear Motion to Rotational Motion Linear • Rotational •
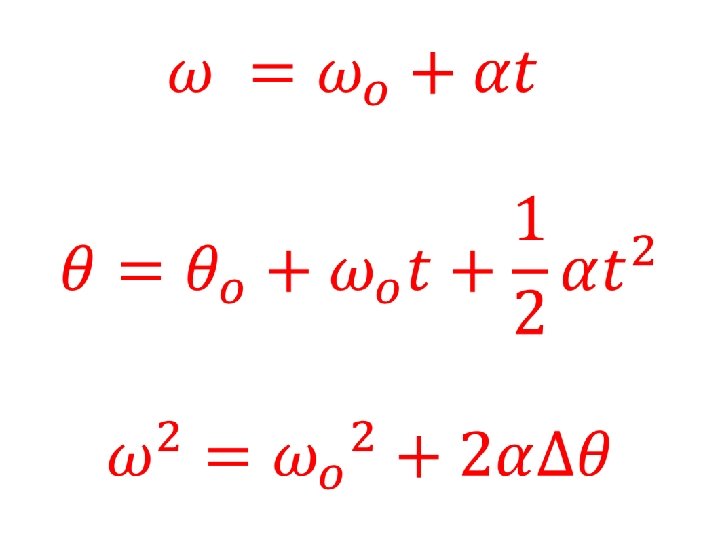

The ride is spinning counterclockwise • Angular velocity vector is way to describe rotational direction without using ‘clockwise’ or ‘counterclockwise’ – It follows a right hand rule • Curl your fingers in the direction the ride is spinning, you thumb points in the direction of the angular velocity vector. • In this case, its UPWARDS

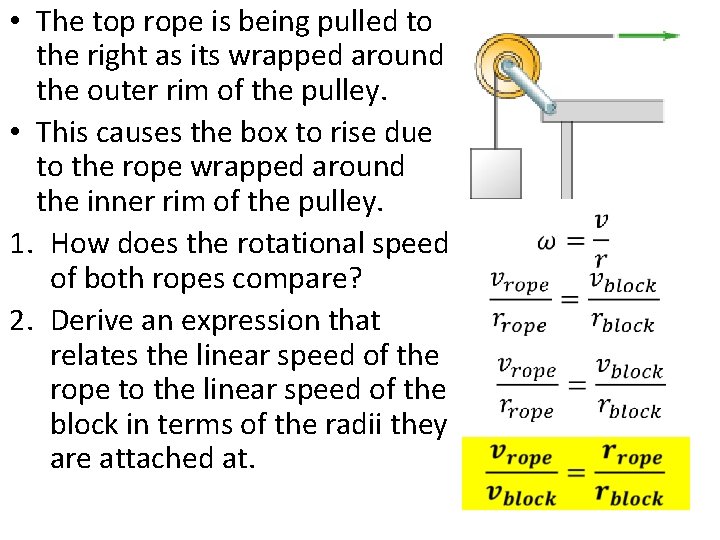
• The top rope is being pulled to the right as its wrapped around the outer rim of the pulley. • This causes the box to rise due to the rope wrapped around the inner rim of the pulley. 1. How does the rotational speed of both ropes compare? 2. Derive an expression that relates the linear speed of the rope to the linear speed of the block in terms of the radii they are attached at.

Motion Graphs

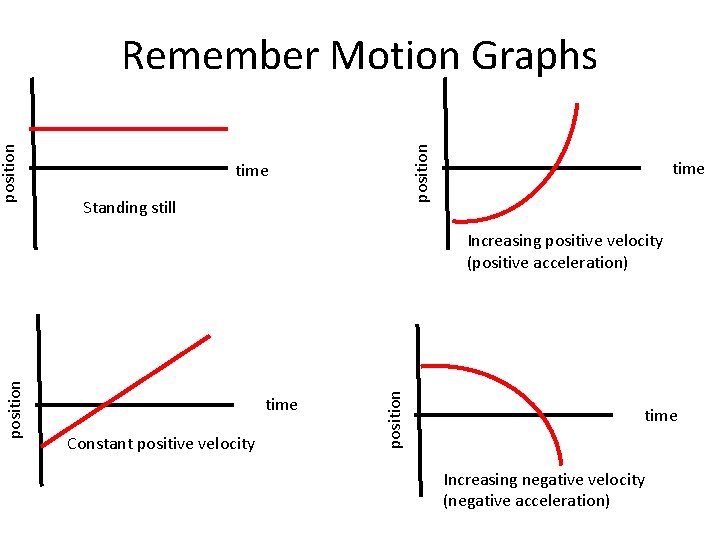
Remember Motion Graphs • Position vs. time – Slope = velocity • Velocity vs. time – Slope = acceleration – Area = displacement • Acceleration vs. time – Area = change in velocity

position Remember Motion Graphs time Standing still time Constant positive velocity position Increasing positive velocity (positive acceleration) time Increasing negative velocity (negative acceleration)

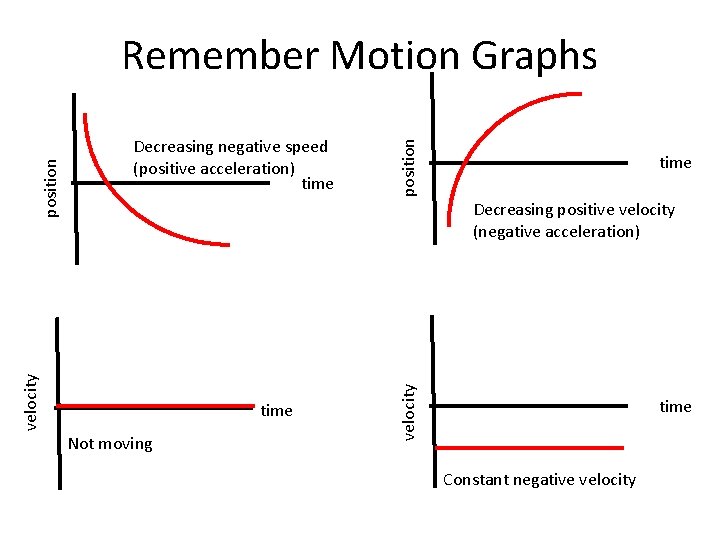
position Decreasing negative speed (positive acceleration) time Not moving velocity Decreasing positive velocity (negative acceleration) velocity position Remember Motion Graphs time Constant negative velocity

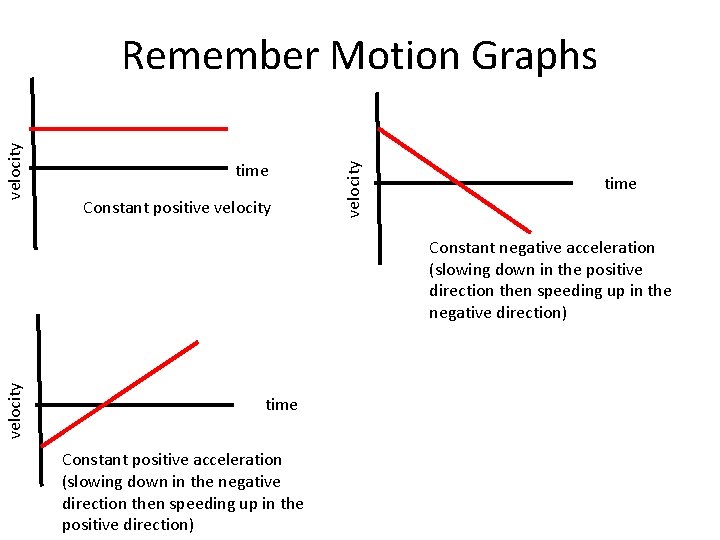
time Constant positive velocity Remember Motion Graphs time velocity Constant negative acceleration (slowing down in the positive direction then speeding up in the negative direction) time Constant positive acceleration (slowing down in the negative direction then speeding up in the positive direction)

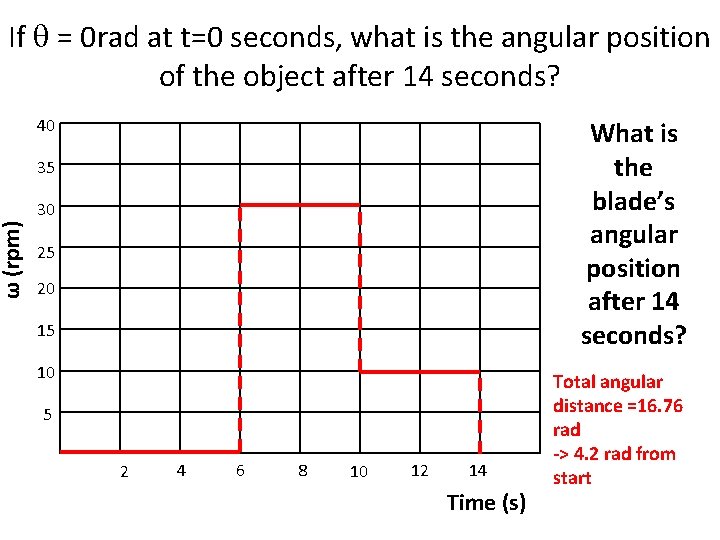
ω (rpm) If = 0 rad at t=0 seconds, what is the angular position of the object after 14 seconds? 40 What is the blade’s angular position after 14 seconds? 35 30 25 20 15 10 5 2 4 6 8 10 12 14 Time (s) Total angular distance =16. 76 rad -> 4. 2 rad from start

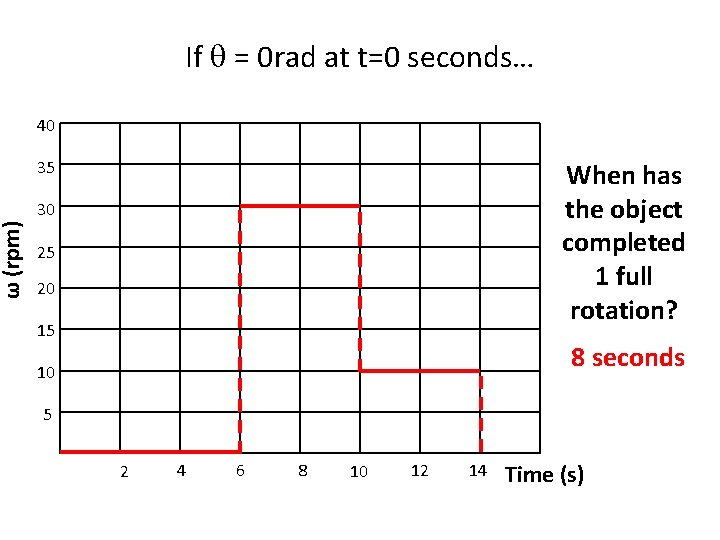
ω (rpm) If = 0 rad at t=0 seconds… 40 35 When has the object completed 1 full rotation? 30 25 20 15 8 seconds 10 5 2 4 6 8 10 12 14 Time (s)

Torque The ‘force’ that makes objects spin.

Torque • F Lever arm Pivot point 1. a force applied ON the pivot point does / does not create torque.

Torque • F Lever arm Pivot point 2. a force applied on the middle of the lever arm does / does not create torque.

Torque • F Lever arm Pivot point 3. a force applied on the right end of the lever arm at an angle does / does not create torque.

Torque • F Lever arm Pivot point 4. a force applied on the end of the lever arm as seen above does / does not create torque.

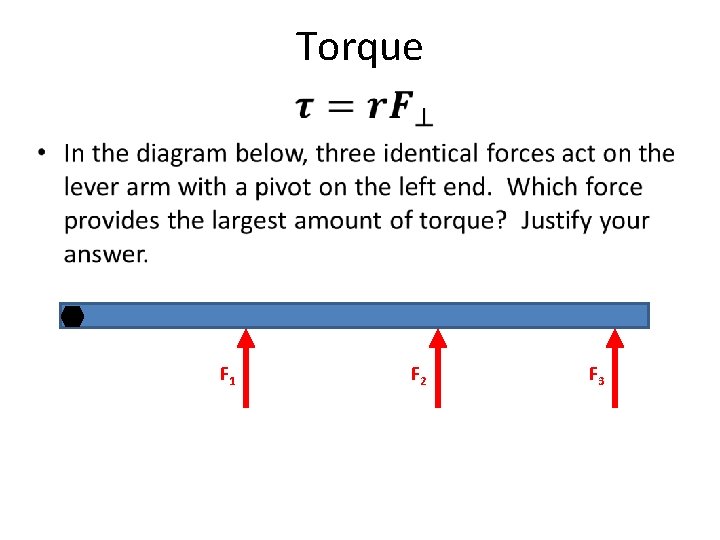
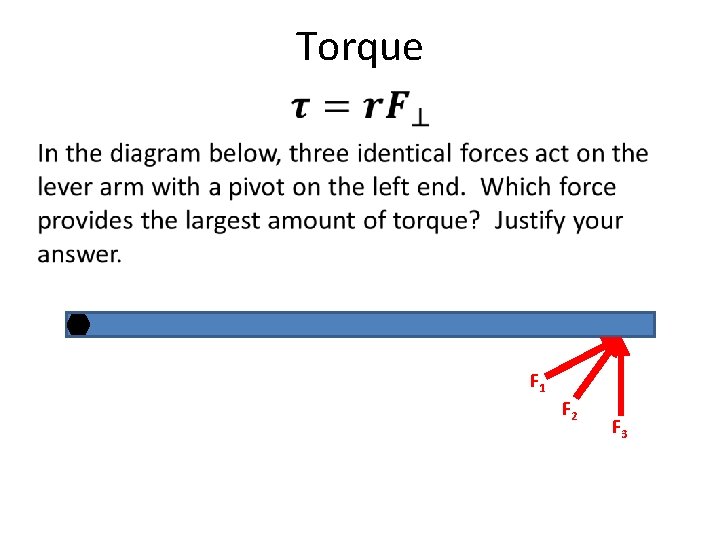
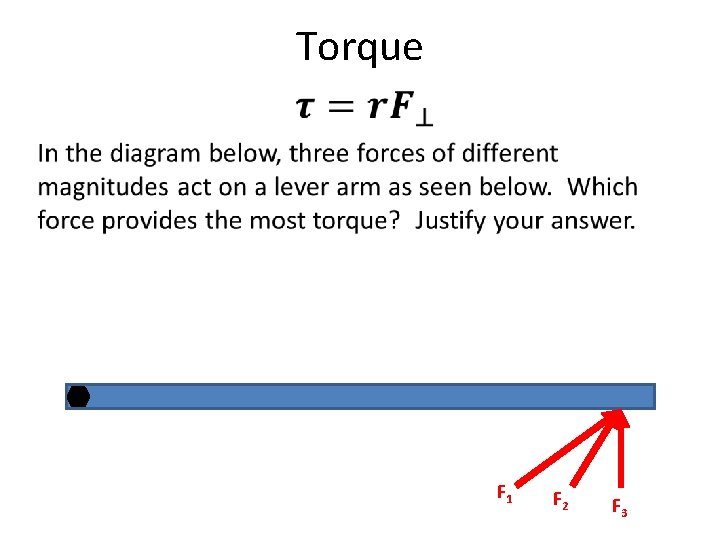
Torque • F 1 F 2 F 3

Torque • F 1 F 2 F 3

Torque • F 1 F 2 F 3

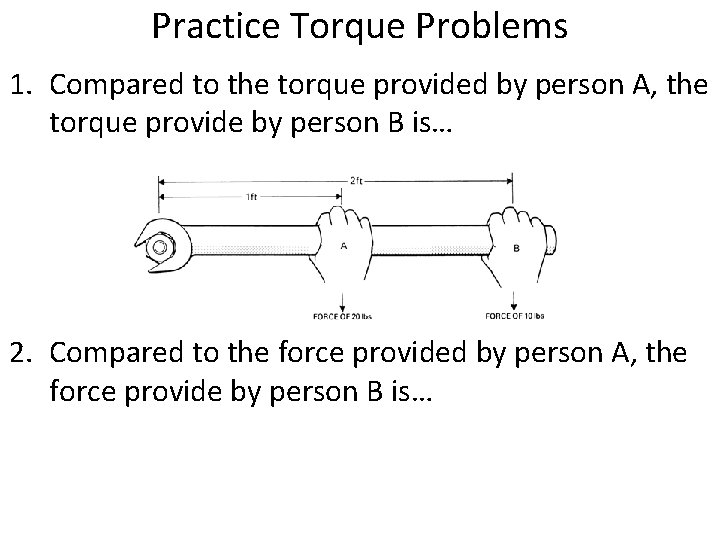
Practice Torque Problems 1. Compared to the torque provided by person A, the torque provide by person B is… 2. Compared to the force provided by person A, the force provide by person B is…

Practice Torque Problems 1. A force of 5. 0 N is applied at the end of a lever that has a length of 2. 0 meters and is pivoted at the opposite end. If the force is applied directly perpendicular to the lever, what is the magnitude of the torque acting the lever? 2. If the same force as in example 1 is applied at an angle of 30 degrees to the horizontal, still at the end of the lever, what will be the magnitude of the new torque?

Practice Torque Problems 1. In order to loosen a rusty bolt, a 120 N force is applied to the mid point of a 18 cm long wrench at an angle of 45 o to the horizontal as seen below. F a. What is the torque applied to the wrench? b. State three things that can be done to increase the amount of torque applied to the wrench. -

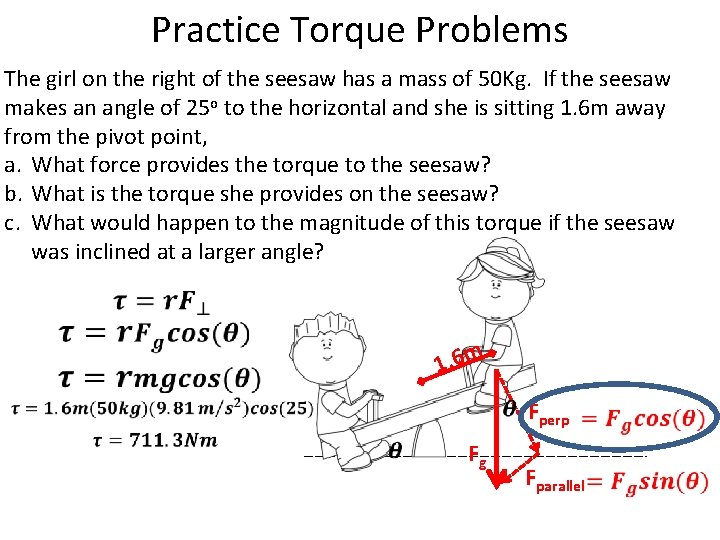
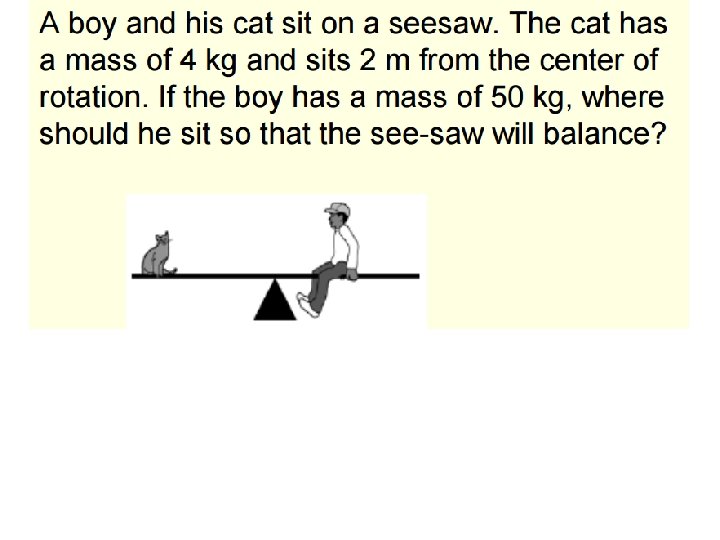
Practice Torque Problems The girl on the right of the seesaw has a mass of 50 Kg. If the seesaw makes an angle of 25 o to the horizontal and she is sitting 1. 6 m away from the pivot point, a. What force provides the torque to the seesaw? b. What is the torque she provides on the seesaw? c. What would happen to the magnitude of this torque if the seesaw was inclined at a larger angle?

Practice Torque Problems The girl on the right of the seesaw has a mass of 50 Kg. If the seesaw makes an angle of 25 o to the horizontal and she is sitting 1. 6 m away from the pivot point, a. What force provides the torque to the seesaw? b. What is the torque she provides on the seesaw? c. What would happen to the magnitude of this torque if the seesaw was inclined at a larger angle? 1. 6 m Fperp Fg Fparallel

Net Torque • Deal with net torque like you would net force. 1. Choose/Locate the pivot point of your system 2. Draw a diagram of all the forces acting on the lever arm and label their distanced from the pivot point!!!! 3. Find the components of all the angled forces 4. The net torque will be all the positive torques minus all the negative torques.

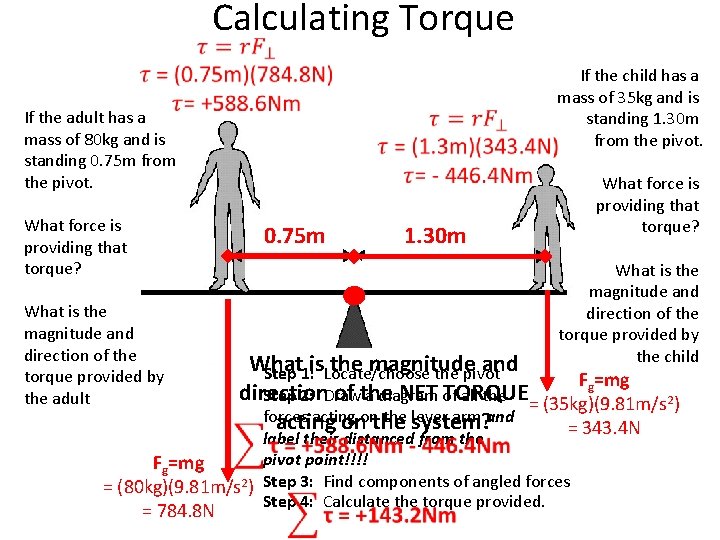
Calculating Torque If the child has a mass of 35 kg and is standing 1. 30 m from the pivot. If the adult has a mass of 80 kg and is standing 0. 75 m from the pivot. What force is providing that torque? 0. 75 m What is the magnitude and direction of the torque provided by the adult What force is providing that torque? 1. 30 m What is the magnitude and direction of the torque provided by the child What the magnitude and Step 1: is. Locate/choose the pivot Fg=mg direction of the NET of TORQUE Step 2: Draw a diagram all the = (35 kg)(9. 81 m/s 2) forces acting the system? lever arm and acting ononthe = 343. 4 N label their distanced from the pivot point!!!! Fg=mg = (80 kg)(9. 81 m/s 2) Step 3: Find components of angled forces Step 4: Calculate the torque provided. = 784. 8 N

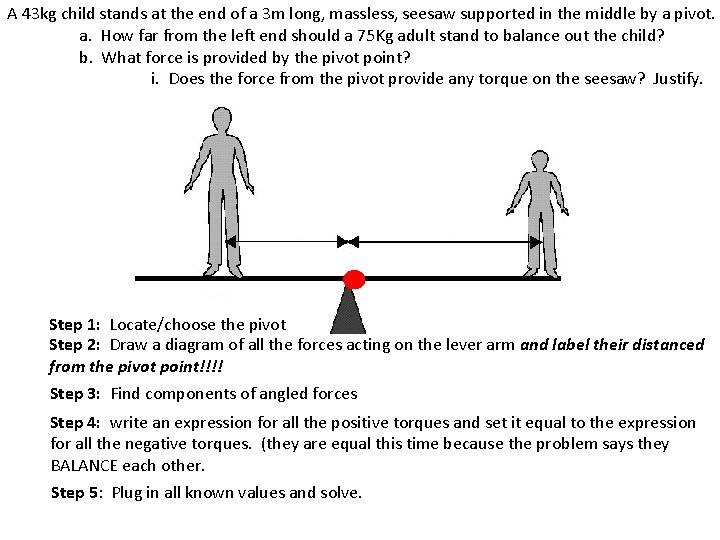
A 43 kg child stands at the end of a 3 m long, massless, seesaw supported in the middle by a pivot. a. How far from the left end should a 75 Kg adult stand to balance out the child? b. What force is provided by the pivot point? i. Does the force from the pivot provide any torque on the seesaw? Justify. Step 1: Locate/choose the pivot Step 2: Draw a diagram of all the forces acting on the lever arm and label their distanced from the pivot point!!!! Step 3: Find components of angled forces Step 4: write an expression for all the positive torques and set it equal to the expression for all the negative torques. (they are equal this time because the problem says they BALANCE each other. Step 5: Plug in all known values and solve.

1. What is the torque provided by the force on the left? 2. What is the torque provided by the force on the right? 3. What is the magnitude and direction of the net torque acting on the rectangular object below? 4. On which end and what force should be added to the object below to keep it in rotational equilibrium?

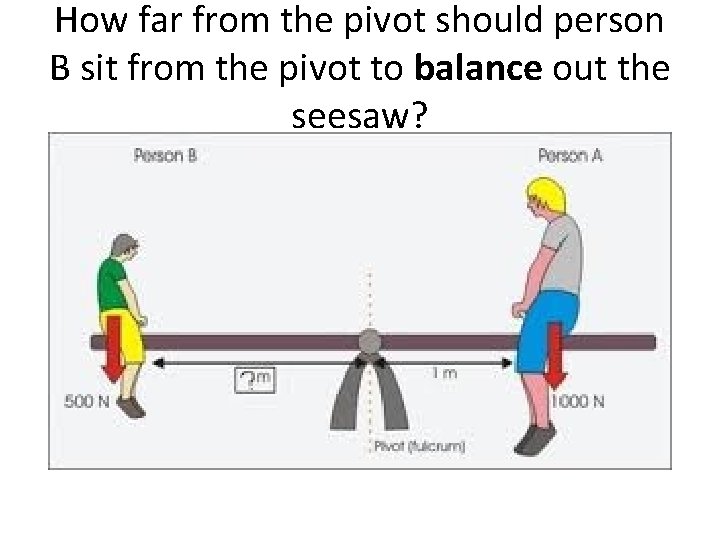
How far from the pivot should person B sit from the pivot to balance out the seesaw?


The girl on the right of the seesaw has a mass of 35 Kg and sits 1. 9 m from the pivot. The boy has a mass of 40 kg and is sitting 1. 5 m from the pivot. If the seesaw makes an angle of 25 o to the horizontal does the boy lift off the ground? JUSTIFY!

Torque on a Massless Pulley A 10 Kg mass is attached to a string wrapped around a massless pulley with a radius of 15 cm. a. What is the torque applied to the pulley? b. What would the torque be if the mass was doubled? c. What would the torque be if the radius of the pulley was doubled?

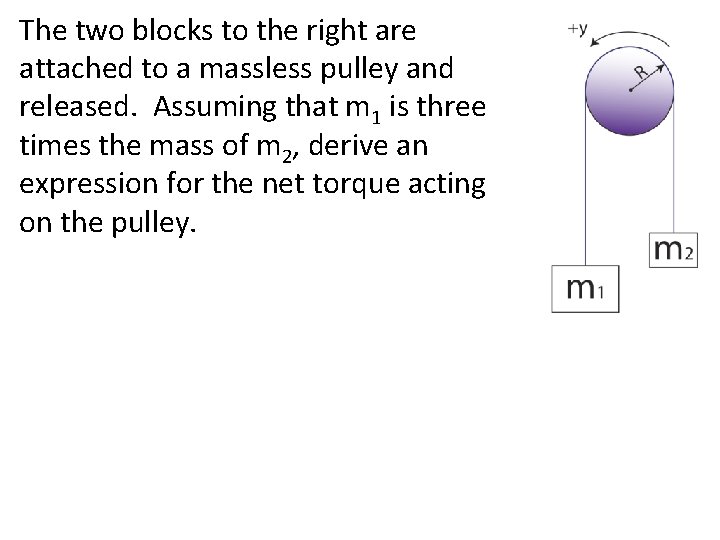
The two blocks to the right are attached to a massless pulley and released. Assuming that m 1 is three times the mass of m 2, derive an expression for the net torque acting on the pulley.

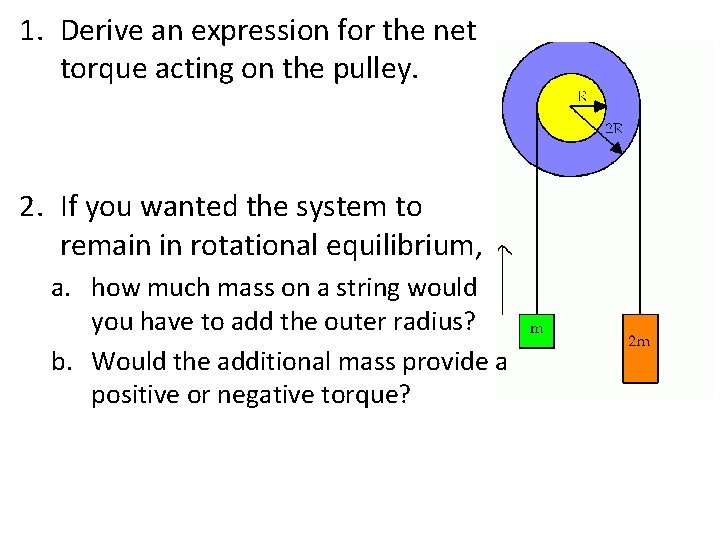
1. Derive an expression for the net torque acting on the pulley. 2. If you wanted the system to remain in rotational equilibrium, a. how much mass on a string would you have to add the outer radius? b. Would the additional mass provide a positive or negative torque?

Mass and Moment of Inertia

Center of Mass - Objects can be considered to have all their mass concentrated in the center. - For objects with mass distributed uniformly the center of mass is actually in the CENTER.

Center of Mass •

A 59 kg woman and a 71 kg man sit on the ends of a massless seesaw that is 3. 5 m long. Where is their center of mass located? • Diagram out the positions of each object • Determine the ‘origin’ • Label the distance from the origin to each object • Apply the center of mass formula in each direction. (in this case, there is only the horizontal direction)

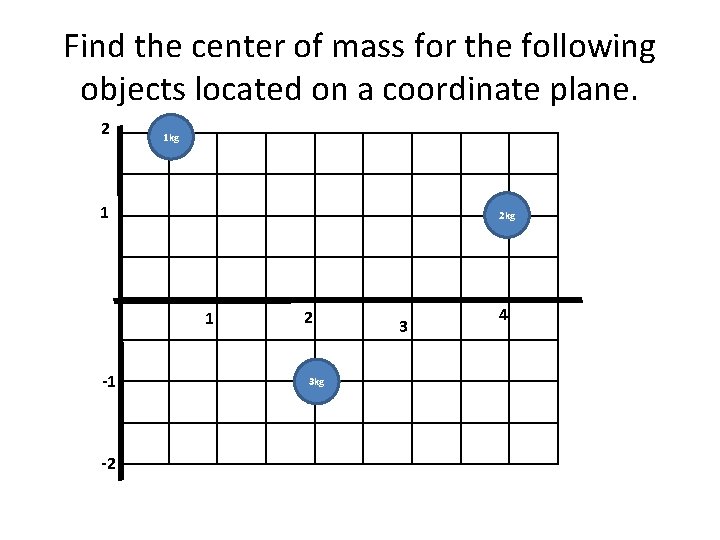
Find the center of mass for the following objects located on a coordinate plane. 2 1 kg 1 2 kg 1 -1 -2 2 3 kg 3 4

Torque Provided by a Center of Mass 20 kg Above is a 20 Kg beam with uniform density that is 12 m long pivoted on the left end. • Where is the center of mass on the beam? • How much torque is provided by the beam’s center of mass? • What force would have to be applied directly upward on the right end of the beam to keep it in ROTATIONAL equilibrium?

Torque Provided by a Center of Mass m=? 20 kg Above is a 20 Kg beam with uniform density that is 12 m long pivoted 4 m from the left end • Where is the center of mass on the beam relative to the pivot point? • How much torque is provided by the beam’s center of mass? • What is the mass of the block placed on the left end of the beam that would keep the beam in ROTATIONAL equilibrium?

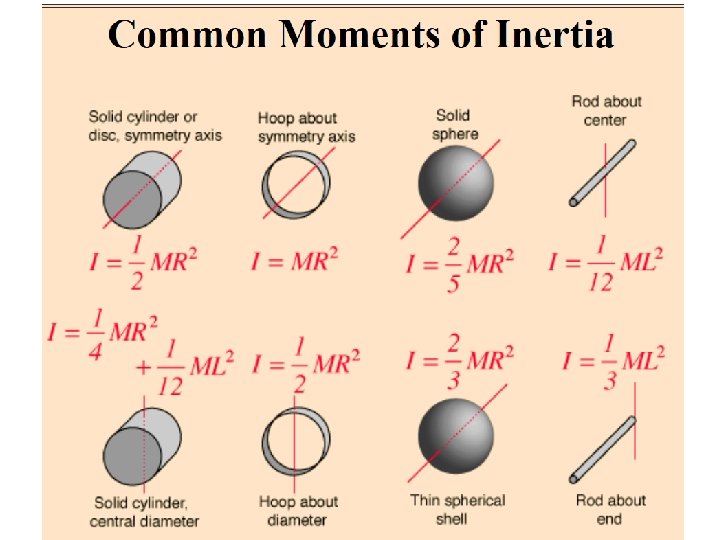
Moment of Inertia •

General Formula for Moment of Inertia •

4 individual 2 kg masses are located as seen above around a massless ring with a diameter of 3 m. • What is the object’s moment of inertia? • What would be the new moment of inertia if the masses were moved halfway towards the center?

Rotational Race Hollow disc Solid disc Two discs - Same radius - Same rotational axis - Same mass - Both start from rest at the top of the hill and are released at the same time. WHICH REACHES THE BOTTOM OF THE HILL FIRST? . . . ask yourself - …Which has a larger rotational inertia? - …What does that mean about how quickly it will start rolling? - …Which will hit first and WHY?

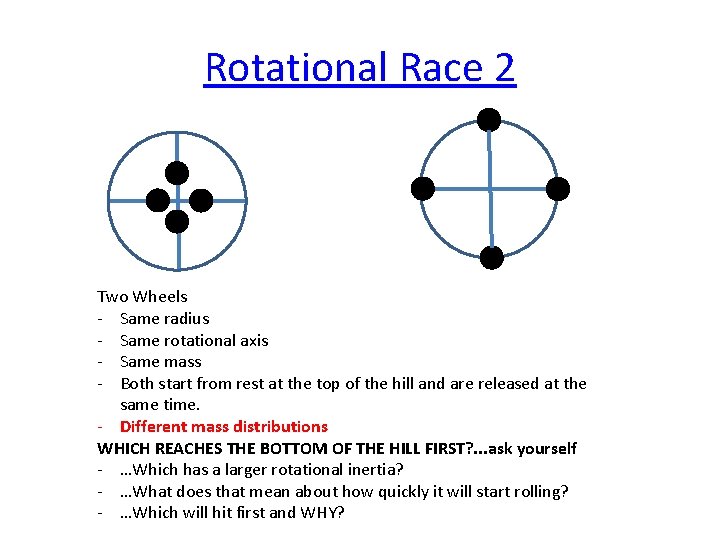
Rotational Race 2 Two Wheels - Same radius - Same rotational axis - Same mass - Both start from rest at the top of the hill and are released at the same time. - Different mass distributions WHICH REACHES THE BOTTOM OF THE HILL FIRST? . . . ask yourself - …Which has a larger rotational inertia? - …What does that mean about how quickly it will start rolling? - …Which will hit first and WHY?




Examples 1. A solid cylinder has a mass of 2 kg and a radius of 13 cm and a length of 26 cm. What is its moment of inertia if a. b. c. It rotates around its symmetry axis It rotates around its central diameter Which orientation would be easier to make rotate? WHY? a. b. c. It rotates around its end? If it rotates around its center? Which would be harder to make rotate? 2. A 4 m long rod has a mass of 1. 3 kg, what is its moment of inertia if

Rotational Dynamics

Linear Fnet=ma Dynamics Rotational τnet=Iα • I is the moment of inertia • α is the angular acceleration

New Definition of Equilibrium • Objects that are in equilibrium must be both in TRANSLATIONAL (linear) equilibrium (left/right and up/down) and in ROTATIONAL equilibrium (clockwise/counter clockwise).

1. A flywheel of radius R = 0. 2 m and mass M = 25 kg is mounted to rotate about its symmetry axis. A rope is wrapped around the wheel and pulled with a force of 10 N. a. What is the wheel’s moment of inertia? b. What is the torque applied to the flywheel? c. What is the wheel’s resulting angular acceleration?

1. 2.

EQUILIBRIUM translational and rotational
